こんにちは、まてがめです。
前回は、分数との違いなども交えつつ小数について解説しました。
小数は10進法をベースにしているので、計算を行う際は自然数の場合とほとんど変わりません。ですが注意しなくてはならない部分もあるので、そこはしっかり押さえていきましょう!
今回は足し算から割り算まで一気に学んでいきますよ!
小数の足し算・引き算
例を使って考えてみましょう。
Aさんは身長が1.7 m、Bさんは身長が1.57 mある。この時、
(1) AさんとBさんの身長の合計は何mになるか?
(2) AさんとBさんの身長差は何mになるか?
(1)
これは足し算ですね。
$1.7+1.57$
筆算を使って計算してみましょう。小数の足し算においても、筆算では位をそろえます。

小さい位から計算していきます。
- 小数点第2位 → そのまま7が下りてきます。
- 小数点第1位 → $5+7 = 12$なので、1が繰り上がり、2が下りてきます。
- 一の位 → 繰り上がってきた1も加えると、$1+1+1 = 3$なので、3が下りてきます。
- 位をそろえて計算しているので、小数点は同じ位置につけます。
よって、答えは3.27 mとなります。
(2)
今度は引き算ですね。
$1.7-1.57$
こちらも位をそろえて筆算を使っていきます。

- 小数点第2位 → 上段に数字がないので、代わりに0があると考えます。小数点第1位を繰り下げ、$10-7 = 3$なので3が下りてきます。
- 小数点第1位 → 上段は先ほど繰り下げたので、$6-5=1$となり、1が下りてきます。
- 一の位 → $1-1 = 0$なので、0が下りてきます。
- 位はそろえて計算しているので、小数点は同じ位置につけます。
よって、答えは0.13 mとなります。
【小数の足し算・引き算】
- 位をそろえて筆算(繰り上がり・繰り下がりに注意)
- 同じ位置に小数点をつける
小数の掛け算
Cさんは身長が1.5 mある。一方、Dさんの身長はCさんの1.12倍だという。
この時、Dさんの身長は何mになるか?
「○○倍」と言っているので、掛け算になります。
$1.5 \times 1.12$
さっそく筆算を使って計算したいところですが、ちょっと待ってください!
掛け算の筆算は足し算や引き算とは異なり、位をそろえて単に上から下へ計算するわけではないので、小数点の位置についてはちゃんと考える必要があります。
そこで、分数を使って次のように式を変形してみましょう。
$\begin{align}
1.5 \times 1.12 & = \dfrac{15}{10} \times \dfrac{112}{100} \\[1.5ex]
& = \dfrac{15 \times 112}{10 \times 100} \\[1.5ex]
& = \dfrac{15 \times 112}{1000}
\end{align}$
これなら分子は自然数の掛け算なので、普通に筆算ができますね。

したがって、
$\begin{align}
1.5 \times 1.12 & = \dfrac{15 \times 112}{1000} \\[1.5ex]
& = \dfrac{1680}{1000} \\[1.5ex]
& = 1.68
\end{align}$
なので、Dさんの身長は1.68 mとなります。小数点の位置も無事決めることができましたね。
【小数の掛け算】
- 分数に直す(小数点以下の桁1つにつき$\frac{1}{10}$)
- 分子を筆算で計算
- 小数に戻す
小数の割り算
人間の身長の世界記録は、およそ2.5 mもあるという。Aさんはその大きさをイメージするため、鉛筆(長さ0.2 m)の本数に置きかえてみることにした。
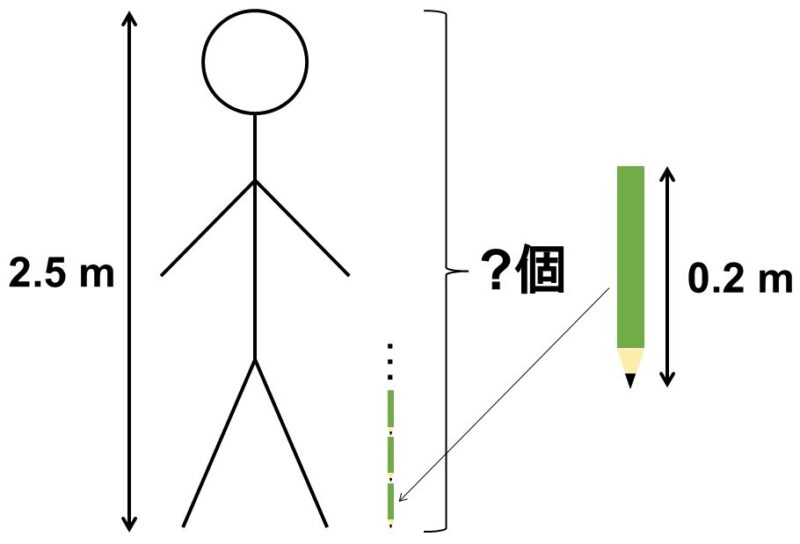
この時、世界記録は鉛筆何本分になるか?
これは次のような割り算として計算できます。
$2.5 \div 0.2$
掛け算と同じく、割り算においても小数点の位置が問題になりますが、これも分数に変形することで考えやすくなります。
$2.5 \div 0.2 = \dfrac{2.5}{0.2}$
ここで、「分数の分母・分子に同じ数を掛けてもよい」性質を使います。
小数点以下は分母・分子のいずれも1桁ですから、分母と分子の両方を自然数にするためには分母・分子に10を掛ければ良いですね。
$\begin{align}
\dfrac{2.5}{0.2} & = \dfrac{2.5 \times 10}{0.2 \times 10} \\[1.5ex]
& = \dfrac{25}{2} \\[1.5ex]
\end{align}$
こうなれば通常の割り算として計算できますね。
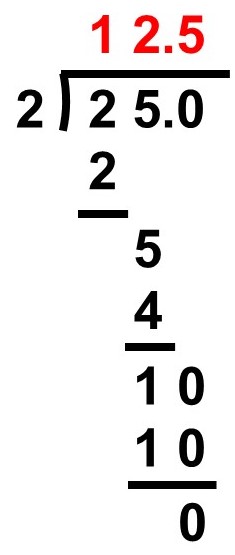
よって、答えは12.5本となります。
【小数の割り算】
- 分数に直す
- 分母・分子が自然数になるように等倍する
- 自然数の割り算として計算する
まとめ
今回は小数の四則演算について学びました。改めて内容をまとめておきましょう。
- 小数の足し算・引き算は自然数の場合と同じ(小数点を忘れないようにする)
- 小数の掛け算は分数に直してから(分子を筆算で)計算し、小数に戻す
- 小数の割り算は分数に直した後、分母・分子を等倍して自然数としてから計算する
足し算・引き算についてはシンプルですが、掛け算・割り算では小数点の位置を気にする必要があるので、そのまま計算しようとせず、分数を使うとわかりやすいです。
今回はここまでです。お疲れさまでした!