こんにちは、まてがめです。
これまでに計算の基礎となる「足し算」と「引き算」を学びました。
これらは四則演算(しそくえんざん)と呼ばれる4つの計算のうちの2つです。つまり、すでに内容の半分が終わっています!この調子で残り2つも学んでいきましょう。
今回からは新たな計算方法として掛け算を学んでいきます。とはいっても、掛け算も足し算をベースにして考えるので、足し算ができればちゃんと理解できます。
足し算や引き算に比べ、掛け算は使える場面を見極める必要がありますが、「足し算がシンプルな形で書ける」という点や「複雑な問題を単純な計算に置き換えることができる」という点で大きな力を発揮します。
掛け算(乗法)とは?
次のような例を考えてみます。
1箱8個入りのチョコを9箱買った。
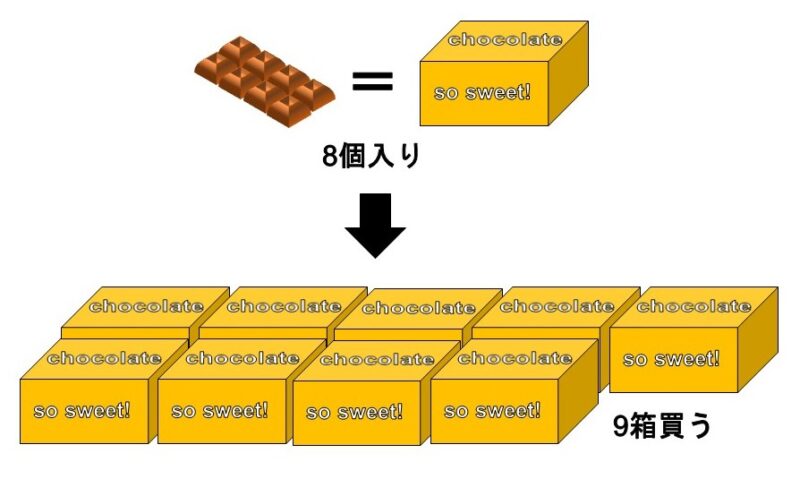
この時、チョコは全部で何個になるか?
まずは、これまでに学んだことを使って数えてみましょう。ここは足し算を使うことで、次のように計算できそうです。
$8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8$
8を9回足すので、式がちょっと長いですね…前から足していきます。
$\begin{align}
& \hspace{13pt} (8 + 8) + 8 + 8 + 8 + 8 + 8 + 8 + 8 \\[1.5ex]
& = (16 + 8) + 8 + 8 + 8 + 8 + 8 + 8 \\[1.5ex]
& \hspace{13pt} \text{…} \\[1.5ex]
& = 72
\end{align}$
よって、答えは72個になります。計算お疲れさまでした。
このように、足し算だけで乗り切ろうとすると計算が大変になることがあります。きっと皆さんの心はこう言っているはずです。
「もっと楽をしたい!」
この「楽をしたい」という気持ちが理学ではとても大切です。「楽をしたい」気持ちがあると「表し方や解き方を工夫しよう!」と考えるからですね。これは理学を進歩させてきた力の1つでもあります。
今回の場合については、すでに先人たちが良い方法を作ってくれています。それが掛け算(乗法ともいいます)です。掛け算の記号×を使うと、先ほどの等式は次のような掛け算に書き直すことができます。
$8 \times 9 = 72$
とてもシンプルになりましたね。×は「左の数に右の数を掛ける」という意味ですが、ピンとこないようであれば「左の数がひとまとまりで右の数だけある」という理解でOKです。また、掛け算の答えは積(せき)と呼びます。
それでは、掛け算が使える場面をもう一つ見てみましょう。
今町Aにおり、町Bを通って町Cに行きたい。町Aから町Bまでの道は4つあり、町Bから町Cへの道は5つある。
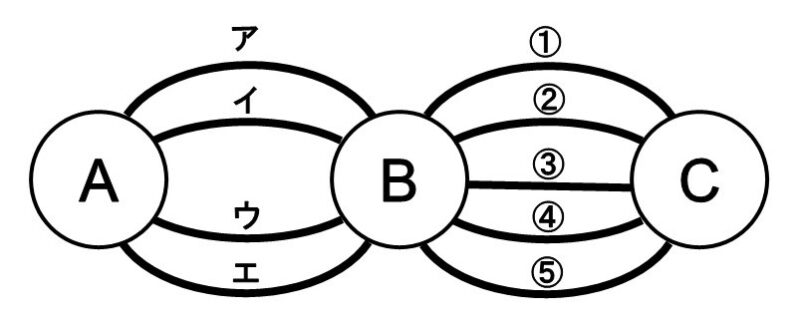
この時、町Aから町Cへの行き方は何通りあるか?
チョコの例よりは少し考える必要がありそうですね。
まず、町Bから町Cへ行くのには➀の道を使うとします。この場合、その手前で町Aから町Bへ行くのにはア~エの4つの道があるので、4通りの方法があることになります。
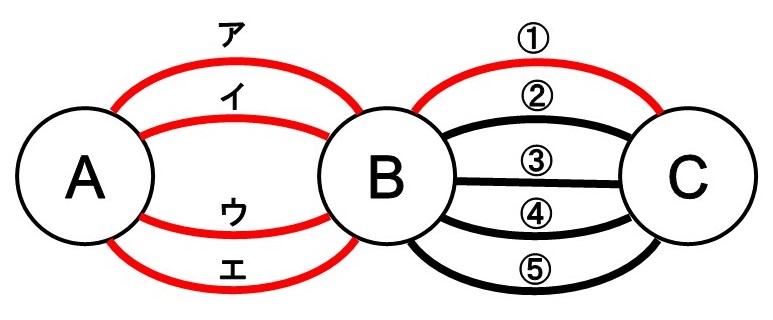
これと同じことが➁~⑤の道についても言える(=それぞれで4通りの方法がある)ので、次のような式で計算できそうです。
$4 + 4 + 4 + 4 + 4$
前から足してみましょう。
$\begin{align}
& \hspace{13pt} 4 + 4 + 4 + 4 + 4 \\[1.5ex]
& = (8 + 4) + 4 + 4 \\[1.5ex]
& \hspace{13pt} \text{…} \\[1.5ex]
& = 20
\end{align}$
よって答えは20通りということがわかります。先ほどではないですが、こちらも計算が長いです。
一方で掛け算を使うと、これは次のように表せますね。
$4 \times 5 = 20$
ここで、この等式をよく見てください。実はこの問題はそんなに難しい話ではなく、「町Aから町Bの道の本数」と「町Bから町Cの道の本数」を単に掛ければ答えが求まるということがわかります。
このように掛け算を使うと、「足し算がシンプルな形で書ける」ことに加えて「一見複雑そうに見える問題を単純な計算に置きかえることができる」というメリットがあります。だからこそ、掛け算は大切なんです。
1~9の数同士の掛け算
掛け算を扱うためには、足し算の時と同じように9×9までの掛け算については覚えておくべきです。ただし、これは学校で先生に「覚えなさい」と言われるから覚えるのではありません。
先ほども言ったように、掛け算のメリットの一つは「大変な足し算で楽ができる」ことです。とにかく楽がしたいんです!
なので、基本的な掛け算は覚えるくらいに慣れていないと、掛け算をするたびに毎回足し算をすることになり、結局掛け算の強みを活かせていないことになってしまいます。
以下に示すのが9×9までの掛け算です。全部で81個ありますが、こちらも足し算の時と同じく×の前後で数字を入れ替えても答えが同じなので、実質45個です。


これも練習方法はいろいろあります。足し算の時に紹介したように、縦横にランダムに数字を書いた表を作って掛け算でマスを埋めていくのも良いと思いますし、よく小学校で習う音読も有効だと思います。下のようなものですね(まてがめはこれで覚えました)。
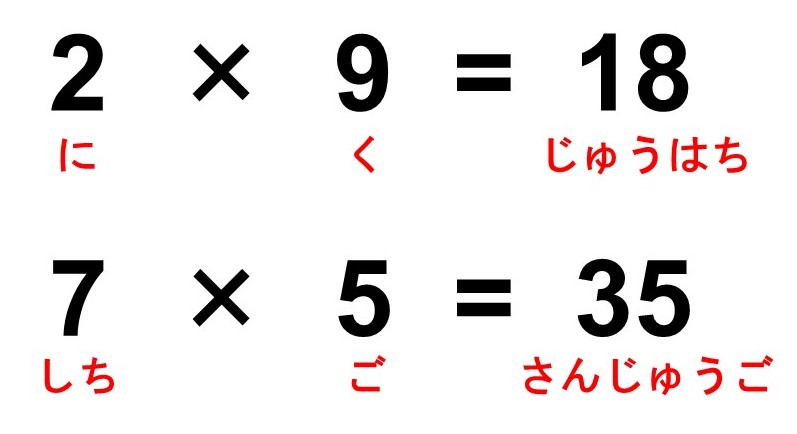
0の入った掛け算は?
掛け算における0の扱いも確認しておきましょう。先ほどのチョコの例を思い浮かべながら考えてみます。
(1) 数に0を掛ける場合
これは1箱も買わなかったということになるので、
$8 \times 0 = 0$
となります。
(2) 0に数を掛ける場合
これは9箱全てが空箱ということになるので、
$0 \times 9 = 0$
となります。
つまり、数に0を掛けても、0に数を掛けても、答えは0になります。
まとめ
今回は掛け算(乗法)について学びました。まとめると次のようになります。
- 掛け算を使うことで足し算がシンプルな形で書ける
- 掛け算を使うことで一見複雑そうに見える問題を単純な計算に置きかえることができる
- 数に0を掛けても、0に数を掛けても、答えは0
「9×9までの掛け算を覚える」ことも確かに大切ですが、「どんな時に掛け算として計算できるのか」を判断できるようになることも同じくらい大切です。しかるべき場面で掛け算が使えれば、いろんな問題を簡単に理解することができるようになります。
今回はここまでです。お疲れさまでした!