こんにちは、まてがめです。
前回は10進法と位取りについて学び、「数を数える」ということができるようになりました。
実は今回学ぶ足し算というのは、この「数える」という操作をより楽に行うための道具です。
足し算を理解することで、数をもっと上手に扱えるようになりますよ。
足し算(加法)とは?
次のような例を考えてみます。
冷蔵庫には卵が3個あったが、お菓子を作るには数が足りなかったので、お店に行って卵を4個買ってきた。
この時、手元にある卵は全部で何個になるか?
ひとまず全ての卵を数えれば求まりそうです。
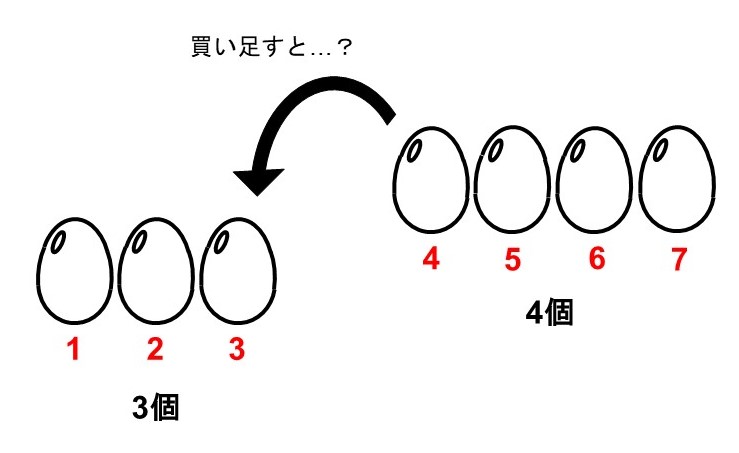
…卵は全部で7個になりますね。
これが足し算です(加法ともいいます)。足し算を表す記号+を使うと、今回の状況を次のような式(しき)として書くことができます。
$3 + 4$
+は「左の数に右の数を足し合わせる」という意味です。今回は卵がもともと3個あるところに新たに4個来たのでこのような書き方になります。
数えた結果は7なので、等しいことを表す記号=(イコール)を使うと、さらに次のような等式として書くことができます。
$3 + 4 = 7$
=は「左側に書いてあること(左辺)と右に書いてあること(右辺)は等しい」という意味です。ちなみに左辺に原因、右辺に結果を書くことが多いです。今回は卵を買い足した結果、全部で7個になったのでこのように書いたわけです。
ちなみに、足し算の答えは和(わ)と呼ばれます。こちらもよく使う言葉なので覚えておいてください。
9+9までの足し算
足し算は基本的に数を数えれば、答え(和)が求まります。例えば9+2であれば、「卵が9個あるところに2個買い足した」と考えて数を数えることで、
$9 + 2 = 11$
と計算できます。ベースにあるのは確かに「数を数える」という操作です。
ただ、それでは足し算を活かしきれていません。実際、足し算をするたびに「1, 2, 3, 4, …」と数えるのは、足し算を行っているというよりも「数を数えている」だけになってしまいます。
足し算が便利なのは、「数える」という操作を実際に数えることなく行うことができるという点にあります。つまり、楽ができるということです。(声を大にして言いたい!)
なので、本当の意味で足し算を活かすためには、基本的な足し算である9+9までの足し算は覚えておく(覚えるくらいに慣れる)必要があります。暗記が苦手な人も、後で楽ができるのでここだけは頑張りましょう。加えて、今後学ぶ計算は足し算がベースになっているので、その理解もしやすくなりますよ。
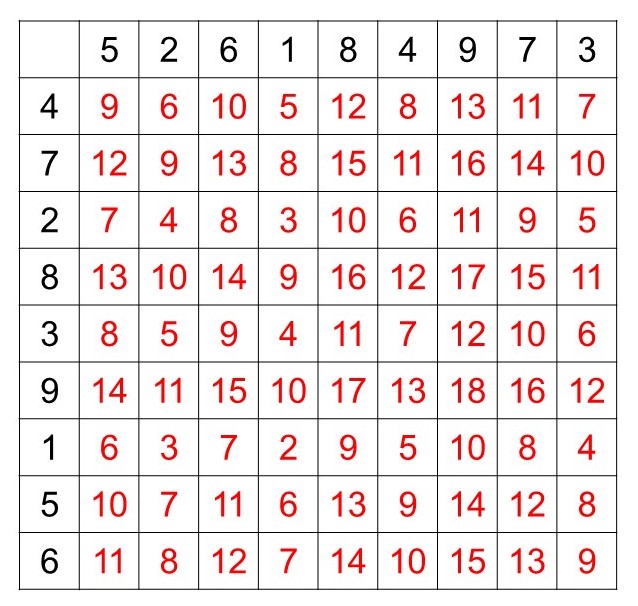
以下に示すのが9+9までの足し算です。全部で81個ありますが、+の前後で数字を入れ替えても答えが同じなので、実質45個ですね。


練習方法はいろいろありますが、例えば縦横にランダムに1から9までの数を書いた表を作り、(縦の数)+(横の数)を埋めていくというのもありだと思います。
0の入った足し算は?
ところで、足し算で0はどう扱われるのでしょうか?先ほどの卵の例で考えてみましょう。
(1) 数に0を足す場合
これは卵を買ってくるのを忘れた場合です。もともと冷蔵庫には3個あったので、
$ 3 + 0 = 3$
となります。
(2) 0に数を足す場合
これは冷蔵庫に卵がなかった場合です。新たに4個買ってくるので、
$ 0 + 4 = 4$
となります。
つまり、数に0を足しても、0に数を足しても、数は変わりません。
複数の足し算
足し合わせるのは1回の計算で1回きりということはありません。次のような場合を考えてみます。
冷蔵庫には卵が3個あったが、お菓子を作るには数が足りなかったので、お店に行き卵を4個買ってきた。ところが後から帰ってきたお母さんも卵を2個買ってきた。
卵は全部で何個になるか?
まとめて数えてみると答えは9個とわかりますが、今回は足し算を使って計算してみましょう。
4個買ってきた後、さらに2個買ってきたので、式は次のようになります。
$3 + 4 + 2$
ちなみに足し算のみの場合、どこから計算しても答えは同じです。
(1)前から計算
$3 + 4 = 7$なので、
$3 + 4 + 2 = 7 + 2$
と書けます。続いて$7+2=9$なので、
$\begin{align}
3 + 4 + 2 & = 7 + 2 \\[1.5ex]
& = 9
\end{align}$
となります。ちゃんと答えが9になりました。
(2)後ろから計算
$4 + 2 = 6$なので、
$3 + 4 + 2 = 3 + 6$
$3 + 6 = 9$なので、
$\begin{align}
3 + 4 + 2 & = 3 + 6 \\[1.5ex]
& = 9
\end{align}$
こちらも9と求まりましたね。
(おまけ)入れ替えて計算
実は計算する順番を入れかえても上手くいきます。例えば、4と2を入れかえて
$ 3 + 2 + 4$
としてみます。
前から計算していくと、$3 + 2 = 5$なので、
$3 + 2 + 4 = 5 + 4$
$5 + 4 = 9$なので、
$\begin{align}
3 + 2 + 4 & = 5 + 4 \\[1.5ex]
& = 9
\end{align}$
やはり答えは9になります。
まとめ
今回は足し算(加法)について学びました。簡単にまとめておきましょう。
- 足し算は簡単に数えるための道具 → 9+9までの足し算は覚えるくらいに慣れる
- 数に0を足しても、0に数を足しても、数は変わらない
- 足し算はどこから計算しても答えが同じになる
足し算はすべての計算の基礎です。前回学んだ「数を数える」という考え方がベースになっていますが、実際に数えなくても数がわかるという足し算の利点が活かせるように練習しておきましょう。
今回はここまでです。お疲れさまでした!