こんにちは、まてがめです。
前回は「数を数える」という考え方から一歩進んで「足し算」という計算方法を学び、9+9までの足し算を覚えることで「実際に数えることなく数がわかるようになる」という話をしました。
では、もっと大きな数(2桁以上の数)の足し算はどうなのかというと、(覚えていれば便利ではありますが)覚える必要はありません。なぜかというと、9+9までの足し算とこれから学ぶ筆算(ひっさん)を使うことで計算ができるようになるからです。
大きな数の足し算
前回学んだ9+9までの足し算ををベースにしてもっと大きな数の足し算についても学んでいきましょう。とはいっても基本的には2パターンしかないので、身構えなくても大丈夫ですよ。
パターン1:繰り上がりのない足し算
次のような例を考えてみます。
「お店で2743円の買い物をした後、帰りに自販機で150円のジュースを買った。」
この時、全部でいくら使ったことになるか?
まずは式にしてみましょう。
$2743 + 150$
大きい数の足し算になってくると、ひたすら数えて答えを出すという力業はさすがに難しいです。時間がかかりすぎますし、数え間違いも起こるからですね。そこでよく使われるのが9+9までの足し算を利用した筆算(ひっさん)です。
筆算ではまず、足し算を行う数について「一の位の下には一の位が、十の位の下には十の位の数が…」というように同じ位をそろえて縦に並べます。同じ大きさの箱(位)同士を並べて計算したいからですね。
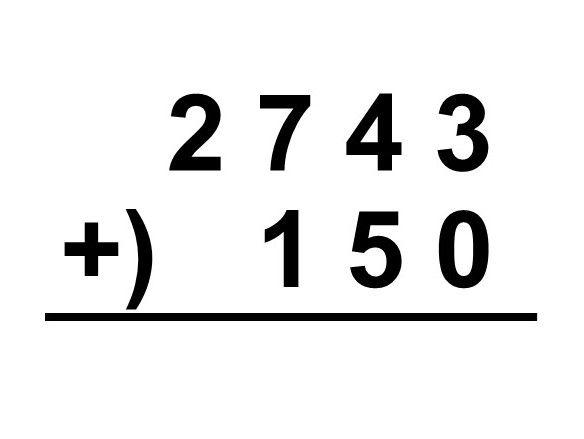
続いて小さい位から順に縦に足し算を行います。一の位は$3 + 0 = 3$、十の位は$4 + 5 = 9$、百の位は$7 + 1 = 8$なので、
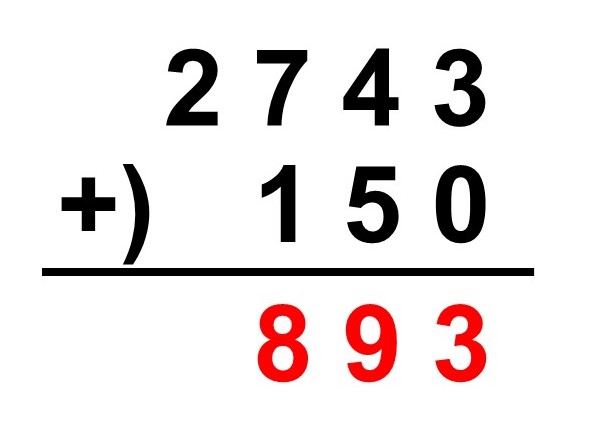
と書けます。最後に千の位ですが、下の段には何もないのでそのまま2を下ろしてきます。
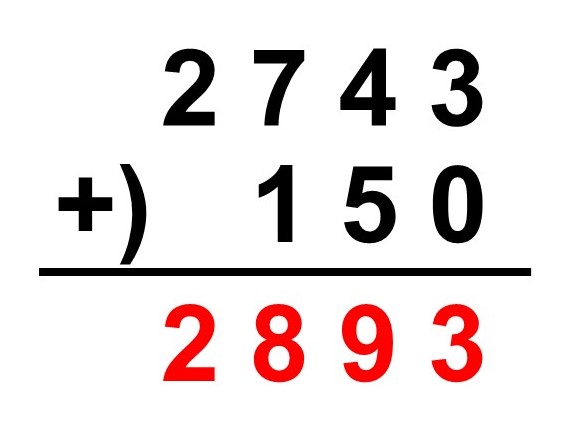
よって、
$2743+150=2893$
であり、答えは2893円となります。
パターン2:繰り上がりのある足し算
今度は次のような例を考えてみます。
「服屋で7480円分の服を買い、その後本屋にも寄って5370円分の本を買った。」
この時、全部でいくら使ったことになるか?
まず、式にすると次のようになります。
$7480 + 5370$
続いて筆算を行います。先ほどと同じように位を揃えて縦に並べ、小さい位から縦に計算していきます。一の位は$0 + 0 = 0$、十の位はというと$8 + 7 = 15$で2桁になってしまいました。
この場合、5だけを下ろして、1は百の位へ持って行きます(上に小さく1と書いておきます)。

これは何をしているかというと、十の位の箱がいっぱいになってしまったので、入りきらない分を百の位の箱に移したということです。位取りの時にも似たようなことをしましたよね?これが繰り上がり(繰り上げ)と呼ばれるものです。
百の位の計算に進みます。先ほど繰り上がった1(つまり100)もあるので、$1 + 4 + 3 = 8$になります。最後に千の位ですが、$7 + 5 = 12$とまたしても2桁になってしまったので、2だけを下ろして、1は一万の位に持って行きます。
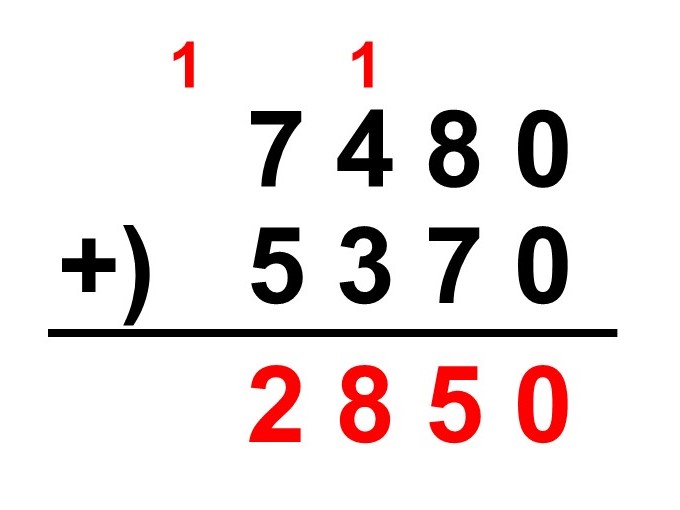
最後に一万の位には繰り上がってきた1があるので、これをそのまま下ろします。
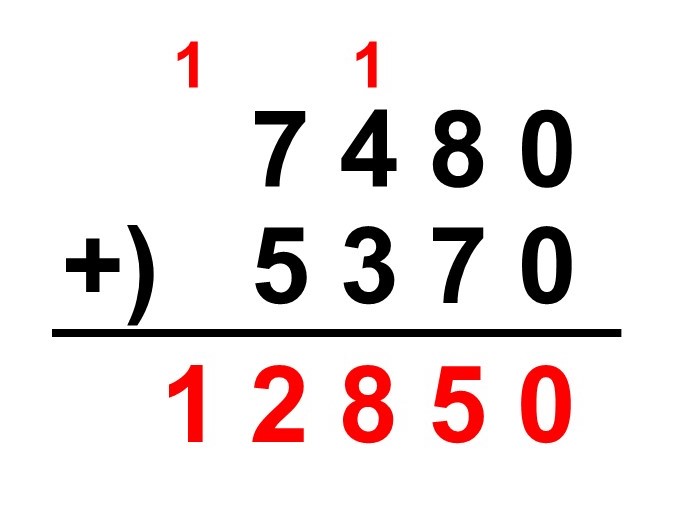
よって、
$7480 + 5370 = 12850$
であり、答えは12850円となります。
筆算の意味
では、どうして筆算で計算できるのかをもう少し掘り下げてみます。先ほどのパターン2の例で見てみましょう。式は
$7480 + 5370$
でした。計算しやすいように7480と5370をそれぞれ箱の大きさ(位)ごとに分解すると、次のようになります。
$7480 = 7000 + 400 + 80$
$5370 = 5000 + 300 + 70$
今度はこれらを縦に足してみます。左辺(=の左側)と右辺(=の右側)でそれぞれ計算すると、
$\begin{align}
7480 + 5370 & = (7000 + 5000) + (400 + 300) + (80 + 70) \\[1.5ex]
& = 12000 + 700 + 150
\end{align}$
となります。わかりやすくカッコを使いました。
すると今度は$12000 = 10000 + 2000$、$150 = 100 + 50$と位ごとに分解できます。ここで出てきた10000と100が繰り上がりに対応しています。出てきた100については、同じ3桁の数である700に加えることで800となるので、
$\begin{align}
7480 + 5370 & = 12000 + 700 + 150 \\[1.5ex]
& = (10000 + 2000) + 700 + (100 + 50) \\[1.5ex]
& = 10000 + 2000 + (700 + 100) + 50 \\[1.5ex]
& = 10000 + 2000 + 800 + 50 \\[1.5ex]
& = 12850
\end{align}$
といった形で答えが求まります。これが筆算で行われている中身になります。長いですね…
大きな数の足し算を行う時、式で書いていくとこうして長くなってしまいますが、筆算を使うとこれを簡単にわかりやすく行えるというわけです。
まとめ
今回は足し算の筆算について学びました。大切なことは次の通りです。
- 位をそろえて縦に並べる
- 繰り上がりがある時は、その分を一つ上の位にまわして計算する
筆算というのは、あくまでも9+9までの足し算を複数回行っているだけです。この範囲の足し算に慣れておけば、大きな数の足し算も必ずできるようになります。
今回はここまでです。お疲れさまでした!