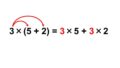こんにちは、まてがめです。
前回は「掛け算が足し算や引き算と一緒に出てきた時の計算の順番」と「分配法則」を学びました。
これら自体はもちろん大切な内容なのですが、実は掛け算における筆算を学ぶための準備でもありました。
2桁以上の大きな数の掛け算にも確かに筆算が役立つのですが、掛け算における筆算は足し算や引き算よりも仕組みが少しわかりにくいです。やり方だけ聞いても、おそらく「(よくわからないけど)そういうものなのかな…」となってしまいます。
ですが、掛け算の筆算には分配法則が使われていることがわかっていれば、筆算の仕組みをちゃんと理解した上で間違うことなく使えるようになります。
筆算で何をしようとしている?
次のような例で考えてみましょう。
電車のある車両には、体重64 kgの大人が38人乗っている。
この時、この車両にかかっている総重量がいくらになるか?
式は次のように書けます。
$64 \times 38$
足し算でひたすら64を38回足すと大変なことになるので、基本的な掛け算で計算できるように工夫します。前回学んだ分配法則を使ってみましょう。
38を位ごとの足し算(30+8)にしてから分配法則を使います。
$\begin{align}
& \hspace{13pt} 64 \times 38 \\[1.5ex]
& = 64 \times (30 + 8) \\[1.5ex]
& = 64 \times 30 + 64 \times 8
\end{align}$
まだ計算しにくいですね。続いて64を位ごとの足し算(60+4)にしてからもう一度分配法則を使います。
$\begin{align}
& \hspace{13pt} 64 \times 38 \\[1.5ex]
& = 64 \times 30 + 64 \times 8 \\[1.5ex]
& = (60 + 4) \times 30 + (60 + 4) \times 8 \\[1.5ex]
& = 60 \times 30 + 4 \times 30 + 60 \times 8 + 4 \times 8 \\[1.5ex]
\end{equation}$
少し長い式にはなりましたが、これなら計算できそうです。前回解説した通り、掛け算→足し算の順に計算していきます。
実は、足し算と同じように複数の掛け算では順番を入れ替えてもどこから計算しても結果が変わりません。このことと「×10で位の0が一つ増える」ことを使って、掛け算の部分をそれぞれ計算してみると、
$\begin{align}
& \hspace{13pt} 60 \times 30 \\[1.5ex]
& = 6 \times 10 \times 3 \times 10 \\[1.5ex]
& = 6 \times 3 \times 10 \times 10 \\[1.5ex]
& = 18 \times 10 \times 10 \\[1.5ex]
& = 1800
\end{align}$
$\begin{align}
& \hspace{13pt} 4 \times 30 \\[1.5ex]
& = 4 \times 3 \times 10 \\[1.5ex]
& = 12 \times 10 \\[1.5ex]
& = 120
\end{align}$
$\begin{align}
& \hspace{13pt} 60 \times 8 \\[1.5ex]
& = 6 \times 10 \times 8 \\[1.5ex]
& = 6 \times 8 \times 10 \\[1.5ex]
& = 48 \times 10 \\[1.5ex]
& = 480
\end{align}$
$4 \times 8 = 32$
ここまでくれば後は足し算だけなので、
$\begin{align}
& \hspace{13pt} 64 \times 38 \\[1.5ex]
& = 60 \times 30 + 4 \times 30 + 60 \times 8 + 4 \times 8 \\[1.5ex]
& = 1800 + 120 + 480 + 32 \\[1.5ex]
& = 2432
\end{align}$
よって、答えは2432 kgです。
つまり式を使って計算する場合、
分配法則を使って計算しやすい形にする → 基本的な掛け算 → 足し算
という手順を踏まなくてはいけません。分配法則の練習にはいいんですけど…やはりちょっと長いです。
これを簡単にしたものが、今から学ぶ筆算になります。
掛け算の筆算
先程の計算式は分配法則を2回使うことで次のように変形できることを確認しました。
$\begin{align}
& \hspace{13pt} 64 \times 38 \\[1.5ex]
& = 60 \times 30 + 4 \times 30 + 60 \ times 8 + 4 \times 8
\end{align}$ …(1)
この例を使って掛け算の筆算を行ってみましょう。
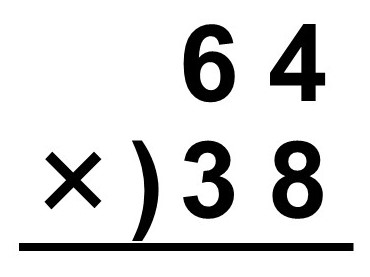
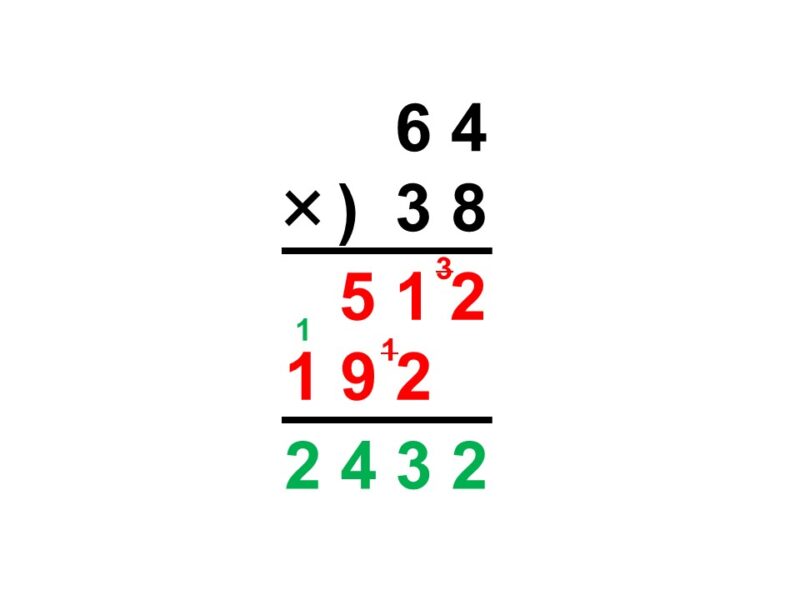
計算の順番ですが、まずは下段の数の一の位に対して上段の数の一の位・十の位を掛けます。
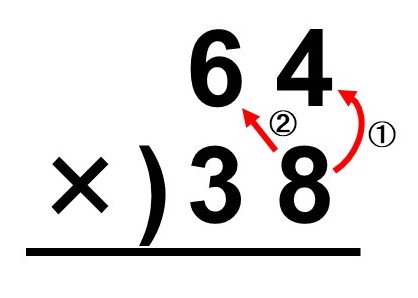
$4 \times 8 = 32$です。なので下には2と書き、繰り上がった3(すなわち30)は後で足すので小さく書いておきます。この計算は式(1)右辺の最後($4 \times 8 = 32$)に対応しています。

続いて$6 \times 8 = 48$(すなわち480)ですが、先ほど繰り上がった3(すなわち30)があるので、これと48を足した数51(すなわち510)を2の隣に書きます。この計算は式(1)右辺の後ろから2番目($60 \times 8 = 480$)に対応しています。

次に下段の数の十の位に対して上段の数の一の位・十の位を掛けます。

$4 \times 3 = 12$(すなわち120)です。なので一番下の十の位の位置(上で1と書いている位置)に合わせて2と書き、繰り上がった1(すなわち100)は後で足すので小さく書いておきます。この計算は式(1)右辺の前から2番目($ 4\times 30 = 120$)に対応しています。

続いて$6 \times 3 = 18$(すなわち1800)ですが、先ほど繰り上がった1(すなわち100)があるので、これと18を足した数19(すなわち1900)を2の隣に書きます。この計算は式(1)右辺の最初($60 \times 30 = 1800$)に対応しています。

最後に一の位から足し算を行います。ここは足し算の筆算と同じように行ってください。

よって、計算結果である2432が得られました。
このように掛け算の筆算は、式(1)のような計算式を簡単に行うためのテクニックだと言えます。
まとめ
今回は掛け算の筆算について学びました。今回は2桁×2桁で説明しましたが、何桁になっても次のように行えばよいです。
- 下段の一の位×上段の一の位、十の位、百の位、…(繰り上がりに注意)
- 下段の十の位、百の位、…についても1と同じように計算する(結果を書く位置に注意)
- 掛け算が終わったら、縦に足し合わせる
筆算に慣れてくるとあまり意識しませんが、やっている計算の中身は元々分配法則から出てくる計算式であるということは理解しておいてください。
やはり筆算はよく使うので、たくさん練習して使い方をマスターしておきましょう!
今回はここまでです。お疲れさまでした!