5F　「大きい数を引く」 ― 引き算における筆算

こんにちは、まてがめです。

前回は新たに「引き算」について学びました。ですが真新しい計算ではなく、足し算の考え方が隠れているという話もしました。

4F　「数を差し引く」 ― 引き算（減法）

足し算と同じく、2桁以上の大きな数の引き算についても筆算を使うことで計算ができます。

足し算の筆算に繰り上がりがあったように、引き算の場合には繰り下がりというものがありますが、こちらは少し操作が増えるので要注意です。

大きな数の引き算
1. パターン1：繰り下がりのない引き算
2. パターン2：繰り下がりのある引き算
筆算の意味
まとめ

大きな数の引き算

こちらも2パターンに分かれるので、順番に見ていきましょう。

パターン1：繰り下がりのない引き算

貯金して18475円貯めることができたので、元々欲しかった本を7250円分買った。

この時、残りのお金はいくらになるか？

式を立てると、

$18475 – 7250$

となります。さっそく筆算を行ってみましょう。

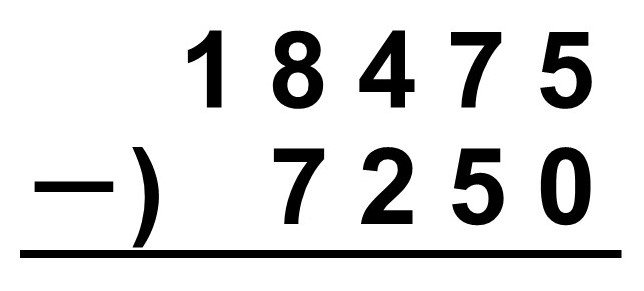
足し算の筆算と同じように、同じ位をそろえて縦に並べ、小さい位から順番に縦に引き算を行います。
一の位は$5-0=5$、十の位は$7-5=2$、百の位は$4-2=2$、千の位は$8-7=1$なので、

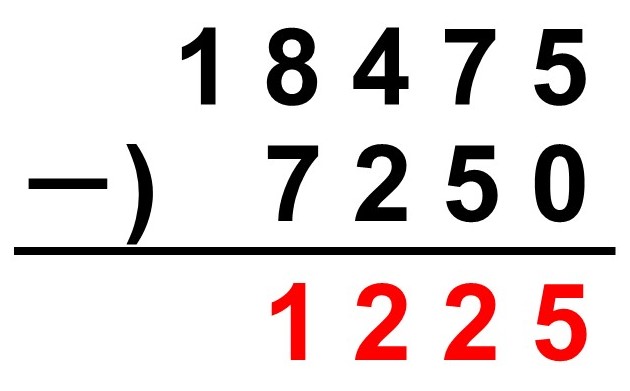
と書けます。最後に、一万の位は下段に何もないのでそのまま1を下ろします。

よって、

$18475-7250 = 11225$

であり、答えは11225円となります。

パターン2：繰り下がりのある引き算

3472人いた来場者のうち、956人が会場から外に出た。

この時、会場にいる人たちは残り何人か？

式にすると

$3472-956$

となります。こちらも筆算を使って計算してみます。

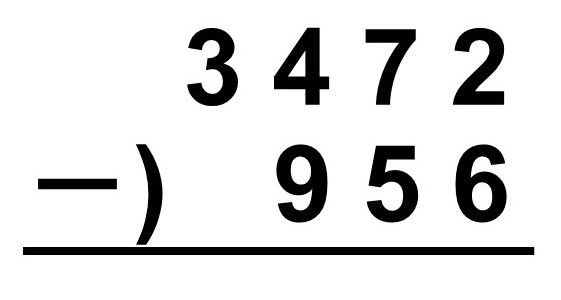
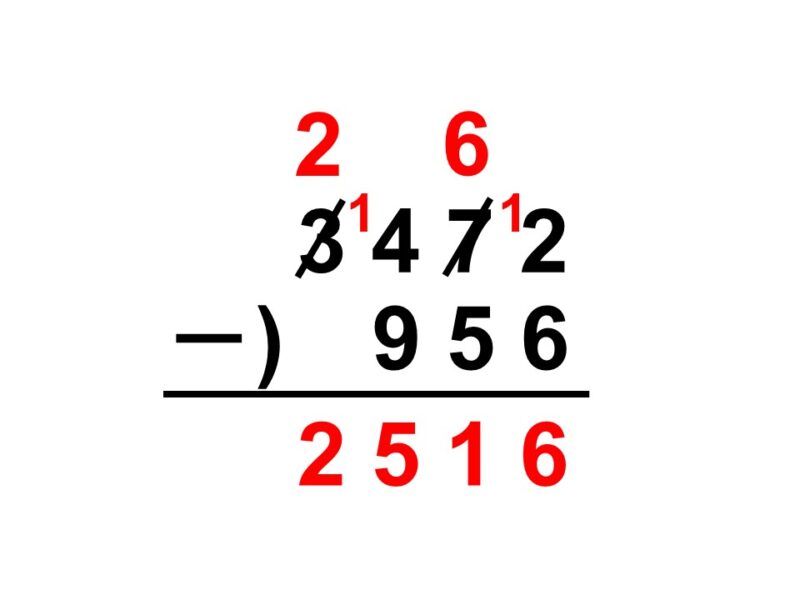
一の位から計算してみると、2－6になってしまいますね。このような時は繰り下がり（繰り下げ）があります。どういうことかというと、一の位は引き算を行うのに数が足りていないので、隣の十の位から10だけもらってくるということです（もらってきた分を小さく1と書いておきましょう）。よって、十の位は7 → 6に繰り下がります。

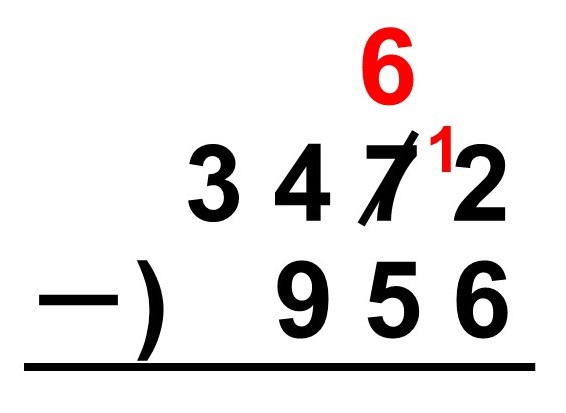
これでひとまず$12-6 = 6$という形で引き算ができます。続いて十の位は7 → 6になっているので、$6-5 = 1$となります。

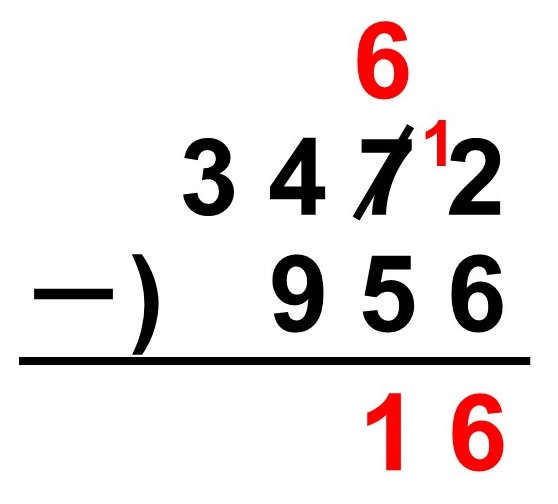
百の位はというと、4－9でまたしても計算できません。なので、今度は隣の千の位から1000だけもらい、$14-9 = 5$（正確には$1400-900 = 500$）として引き算を行います。千の位では3 → 2に繰り下がるので、2をそのまま下ろしてきます。

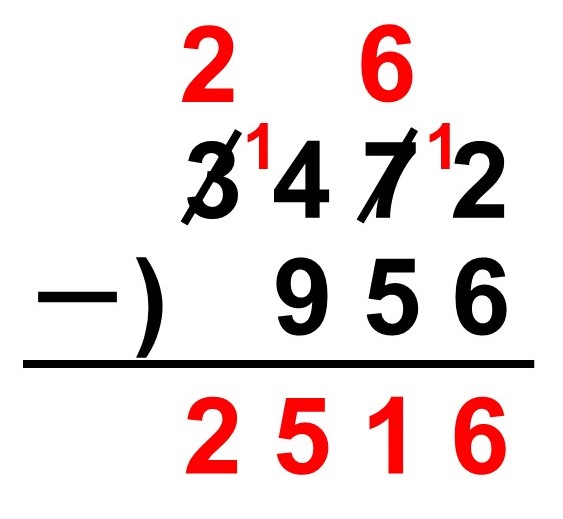
よって、

$3472-956 = 2516$

なので、答えは2516人となります。

繰り下がりは足し算での繰り上がりと真逆のことなのですが、操作が少し増えるので、もしかしたらこちらの方が難しいと感じる人が多いかもしれませんね。

筆算の意味

引き算の筆算で何が行われているのかについて、もう少し掘り下げて見てみましょう。

パターン2の計算式で考えます。

$3472-956$

まずは、3472と956を各位の足し算に分解します。

$\begin{align}
3472 & = 3000 + 400 + 70 + 2\\
956 & = 900 + 50 + 6
\end{align}$

続いて、縦に引き算を行います。左辺（＝から左側）と右辺（＝から右側）でそれぞれ計算すると、

$3472-956 = 3000 + (400-900) + (70-50) + (2-6)$

同じ位ごとにカッコで整理しましたが、このままでは百の位と一の位ではカッコの中身が計算できません。なので、まだ余力がある千の位と十の位に助けてもらいます。つまり、$3000 = 2000 + 1000$、$70 = 60 + 10$とし、この1000と10を足りていないところに回します。これがまさに「繰り下がり」です。

$\begin{align}
3472-956 & = 3000 + (400-900) + (70-50) + (2-6) \\[1.5ex]
& = (2000 + 1000) + (400-900) + ((60 + 10)-50) + (2-6) \\[1.5ex]
& = 2000 + (1000 + 400-900) + (60-50) + (10 + 2-6) \\[1.5ex]
& = 2000 + (1400-900) + (60-50) + (12-6)
\end{align}$

これですべて計算できるようになりました。よって、

$\begin{align}
3472-956 & = 2000 + (1400-900) + (60-50) + (12-6) \\[1.5ex]
& = 2000 + 500 + 10 + 6 \\[1.5ex]
& = 2516
\end{align}$

となります。やはり式で書いていくと大変ですね。ぜひとも筆算を使いこなして楽しちゃいましょう。