こんにちは、まてがめです。
今回から数学(あえて算数との区別はつけないことにしています)を学んでいきますが、あなたに質問です。
一から数学を学ぶとなった時、最初に学ぶべき考え方とは何でしょうか?
…答えを言ってしまうと、それは「数える」という考え方です。
「そんなことはさすがにわかるよ」という方もいるかもしれませんが、やっぱり「数学」というくらいですから、まずは「数」について深く理解しておくべきですよね。
実際、なぜ「数」というものがあるのか、そしてなぜ「数える」ことができるのか、考えてみたことはありますか?
私たちの世界では、モノを数えたり、数を計算したりと特に意識することなく「数」が使われていますが、その仕組みはとてもうまく作られています(最初に考えた人は天才です)。
今回は、その仕組みである10進法と位取りについて学びます。
物を「数える」ということ
ここにリンゴがあります。
もし「数える」ということを知らない人が見たら、ただ「リンゴがある」としか思いません。
でも「数える」ということが分かるようになると、例えば「リンゴが3個もある!(1個だけ食べちゃおうかな…)」というように考えることができます。
つまり、「数」やモノを「数える」という考え方を学ぶことで、その様子をより詳しく理解したり、他の人にこれを伝えたりできます。これは便利ですよね。
「数」を対応させる
物を数えるためには、モノの様子と数を対応させる必要があります。つまり、「どういう時」にリンゴが「〇個ある」と判断するか、ということです。
対応させる方法は色々あるのですが、現代ではアラビア数字というものがよく使われています。これを使うと、
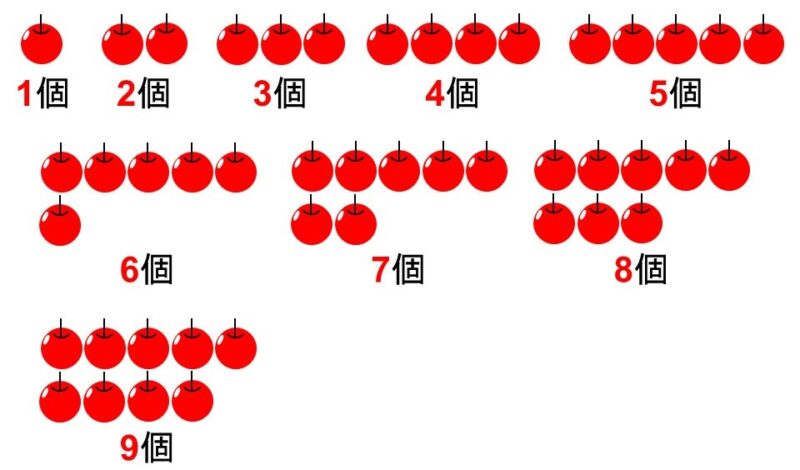
というように対応できます。これで1から9までモノを数えることができるようになりました。
ちなみに、リンゴが「全くない時」はどう表したらよいでしょうか。これはアラビア数字で
0
と表します。
「…そもそも何もない状態を表す意味なんてあるのか?」と思う人もいるかもしれませんが、0という数にはもう一つ重要な役割を持っています。それが位取り(くらいどり)です。
位取りと10進法
さて、9よりも大きい数はどう数えればよいのでしょうか?ここにたくさんのリンゴがあります。何個あるのか数えてみましょう。
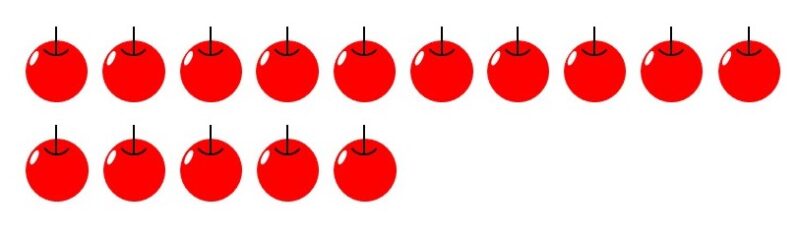
とりあえず9個までは数えられますよね。次の1個を数える時は、一度0を書いてから左隣に1を書くことで、
10
とします。このような書き方を位取り(くらいどり)といいます。
これを理解するには、箱をイメージするとよいと思います。「リンゴを箱に入れていって、箱がいっぱい(=9を超える)になったら、左隣に大きな箱を用意して全部移しかえる」といった感じでしょうか。
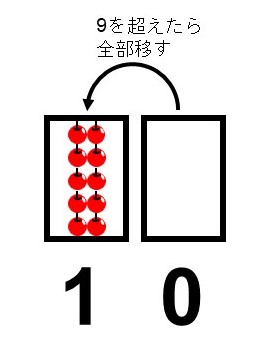
10個よりも1個多い時は、0→1にして
11
と数えていきます。この方法を使うと、最終的にリンゴの数は15個と分かります。
では、次はどうでしょうか?

…ひとまず19個までは数えられますよね。次の1個を数える時は、一度0を書いてから左隣に2を書くことで、
20
とします。だんだんと仕組みが分かってきたでしょうか?20個よりも1個多い時は、再び0→1にして
21
と数えていきます。結果として、リンゴの数は23個と分かります。
このように10という数をまとまりにして数を数えていく方法は10進法と呼ばれています。人間の指がちょうど全部で10本あるからこうした方法が使われるのでしょうね。
より大きな数を数える ― 0と位取りの力
位取りという考え方にまだピンと来ていない方もいるかもしれないので、もっと大きい数を数えることで理解を深めましょう。
10進法を使うと、こんなふうに数を数えていくことができるはずです。
1, 2, 3, 4, 5, 6 ,7, 8, 9, 10, 11, 12, …
…88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99
この次はどうするかというと、まず0を2つ書いてから左隣に1を書くことで、
100
と数えます。そしてその後は、
101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, …
…988, 989, 990, 991, 992, 993, 994, 995, 996, 997, 998, 999, 1000…
と続いていきます。
ここでも箱をイメージすると分かりやすいです。99から1増やす時、右端の箱がいっぱいなので、まず左隣の箱に全部移しかえて空にします(0を書く)。すると今度は左側の箱もいっぱいになってしまうので、その左隣にもっと大きな箱に全部移しかえて空にします(左にもう一つ0を書く)。左端の箱には新しいまとまりがやって来たのでこれを1と数えます(1を書く)。
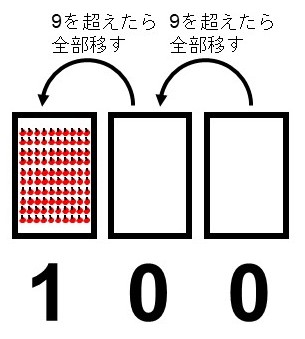
このようにしてどんどん大きな数を数えていけます。0という数字は、ここでいう箱をイメージしながら位取りを行っていくのにとても便利なんですよね。これが0のもう一つの役割です。
もし0という数を作らずに数を数えようとすると、10以上の数に対してもそれを表すための数字を新しく作らないといけません。でもそれだと数字を全部覚えるのが大変です。
つまり0と位取りのおかげで、0から9の数字だけ覚えておけば、数をいくらでも数えることができるということです。何度も言いますが、最初にこれを考えた人は天才だと思います!
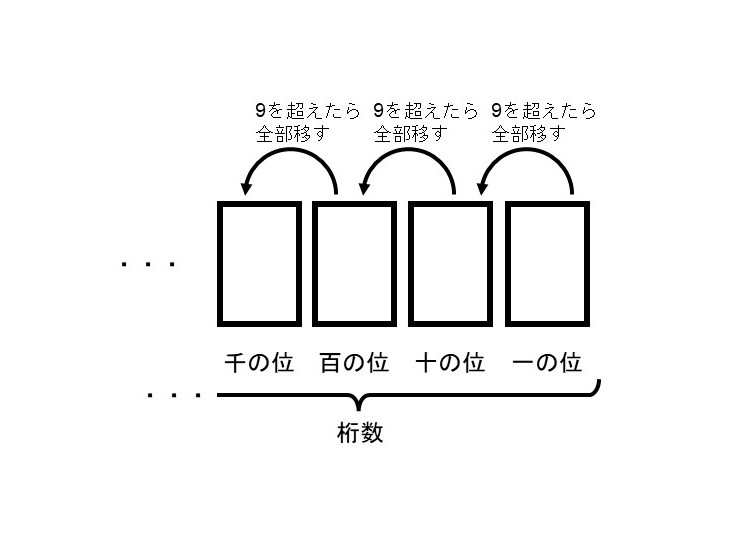
各位の名前と桁数
先ほどはイメージしやすいよう箱を考えることで位取りについて理解を進めてきましたが、この箱には名前がついていて、右端から一の位、十の位、百の位、千の位、…と呼びます。また、使っている箱の数のことを桁数(けたすう)と呼びます。
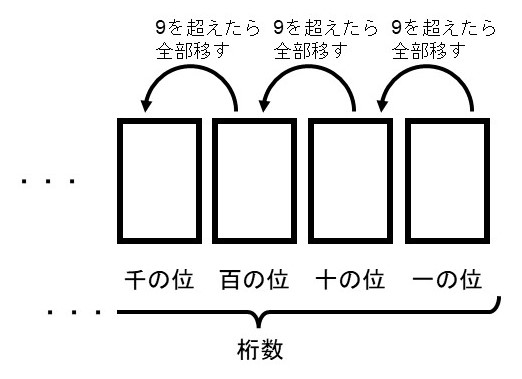
次の数を例に考えてみましょう。
2507
この場合、
- 一の位…7 / 十の位…0 / 百の位…5 / 千の位…2
- 桁数…4
となります。今後よく使う言葉なので覚えておいてください。
まとめ
今回は10進法と位取りについて学びました。
- 10進法は「10という数をまとまりにして数を数える方法」
- 位取りは「箱(位)がいっぱいになったら左隣へまとめて移しかえる」
現代では当たり前に使われている考え方ではありますが、こうして見てみると本当に上手くできているなと感じます。あなたもぜひ古代の先人に思いをはせながら、数字を使ってみてください。
さて、「数」という考え方を理解したことで、私たちは次に「数を使って計算する」ということができるようになります。次回からは、この「計算」について学んでいきます。
今回はここまでです。お疲れさまでした!