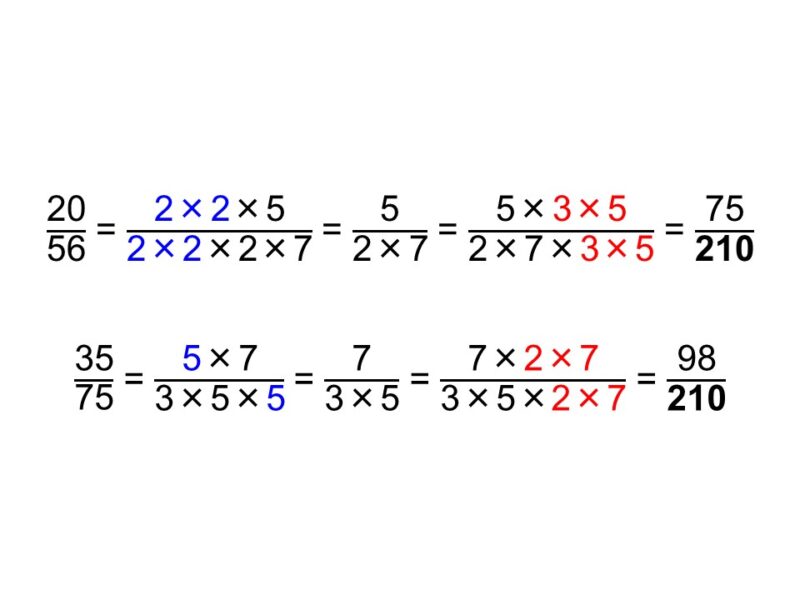こんにちは、まてがめです。
前回は、数に対する新しい考え方として「分数」について学びました。
特に、分数は「数」でありながら「割り算」でもあるというのが大きなポイントでしたね。
この「分数」を使って、さっそくいろいろな問題に取り組みたいところなのですが、私たちが分数を扱うにはまだ1つ大きな問題があります。それは「分数の大小がわからない」ということです。
例えば、「17と28のどちらが大きいか?」と言われれば、「28の方が大きい」とすぐにわかります。これは10進法と位取りを理解していれば、どうやって数が大きくなっていくのかがわかるからですね。
ですが、次の2つの分数はどちらが大きいかわかるでしょうか?
[1] $\dfrac{20}{56}$ [2] $\dfrac{35}{75}$
「数の大小がわかる」ことは数を扱っていく上で欠かせませんが、今の私達では分数の大小をどう比べたらよいのかわかりません。
これを解決するための道具となる素因数分解(そいんすうぶんかい)と約分(やくぶん)・通分(つうぶん)について学んでいきましょう。
分数の大小を比べるための準備
準備1:分数の性質
分数には次の2つの性質があります。
- 分母と分子に同じ数を掛けても、その分数は変わらない
- 分母と分子を同じ数で割っても、その分数は変わらない
(例1)
$\dfrac{5}{8} = \dfrac{5 \times 4}{8 \times 4} = \dfrac{20}{32}$
(例2)
$\dfrac{12}{54} = \dfrac{12 \div 6}{54 \div 6} = \dfrac{2}{9}$
なぜ分数にこのような性質があるのでしょうか?具体例を考えてみます。
(1) 1 Lの牛乳1本を3人分に分けたい。
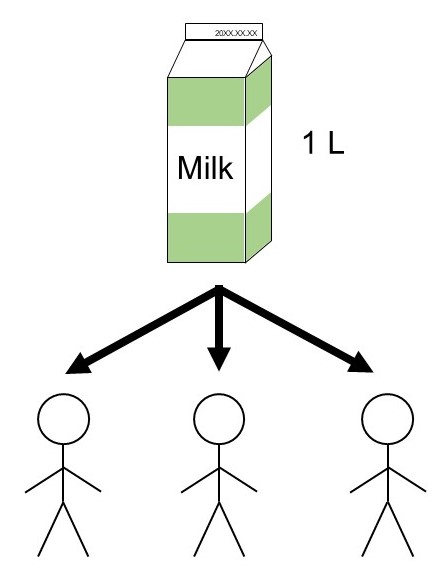
この時、1人分の量は次のように書けます。
$1 \div 3 = \dfrac{1}{3}$ L
では、次の(2)ではどうでしょうか?
(2) 1 Lの牛乳3本(3 L)を9人分に分けたい。
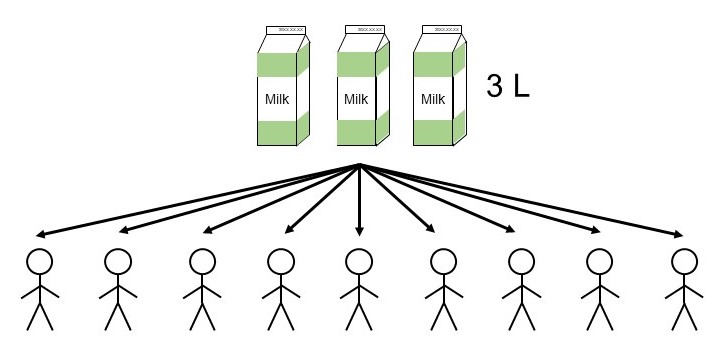
この時、1人分の量は次のように書けます。
$3\div9=\dfrac{3}{9}$ L
ここで(2)をよく見てみると、この状況は(1)を3倍したもの(=分母×3・分子×3)と考えることもできます。
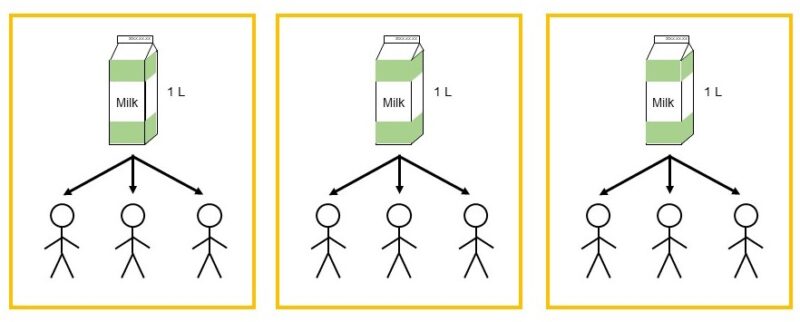
ということは、1人分の量は変わりません。よって、
$\dfrac{1}{3} = \dfrac{1 \times 3}{3 \times 3} = \dfrac{3}{9}$
が成り立ちます。
これは逆に見ることもできます。すなわち、(1)は(2)を3等分したもの(=分母÷3・分子÷3)であると考えることができるので、
$\dfrac{3}{9} = \dfrac{3 \div 3}{9 \div 3} = \dfrac{1}{3}$
が成り立ちます。
このように、分数において「分母と分子に対して同時に掛け算をしたり同時に割り算をしたりするだけであれば状況そのものが変わることはない」ので、分数が変わることもないというわけです。
準備2:素因数分解
素因数分解(そいんすうぶんかい)とは、数を素数(そすう)の積で表す操作です。簡単に言えば、ある数を「できるだけ小さい数の掛け算に分解する」ということです。
素因数分解の例をいくつか見てみましょう。
(例1)
$6 = 2 \times 3$
(例2)
$30 = 2 \times 3 \times 5$
(例3)
$169 = 13 \times 13$
「素因数分解する」=「素数の積で表す」と言いましたが、それはつまり「どんな素数でなら割り切れるかを探す」ということでもあります(掛け算と割り算の関係を覚えていますか?)。
なので素因数分解をしようと思ったら、まず適当な素数で割ってみるのがよいです。
先ほどの例2で扱った「30の素因数分解」を実際にやってみましょう。
(1) 素数で割れるか調べる
試しに一番小さい素数である2で割ってみます。すると$30 \div 2 = 15$なので、
$30 = 2 \times 15$
よって、30は2と15の積になることがわかりました。
(2) 商が素数で割れるか調べる
今度は15が素数で割れるか調べます。例えば$15 \div 3 = 5$なので、
$15 = 3 \times 5$
よって、15は3と5の積になることがわかりました。
(3) まとめる
(1)と(2)から、30は2, 3, 5の積であることがわかりました。よって、次のように素因数分解できます。
$30 = 2 \times 3 \times 5$
ちなみにこの結果から、「30は2, 3, 5を素因数に持つ」という言い方をすることがあります。「30は2, 3, 5という素数から作られている」という意味ですね。
分数の大小を比べてみよう
お待たせしました。ようやく準備ができたので、分数の大小を比べてみましょう。
最初に示した分数はこの2つでした。
[1] $\dfrac{20}{56}$ [2] $\dfrac{35}{75}$
ステップ1:素因数分解
[1]の分数から考えてみましょう。分母:56、分子:20なので、この2つを素因数分解します。
何も思いつかない時は適当な素数で割ってみるのが確実ですが、9×9までの掛け算を覚えているのであれば、どんどん利用しましょう。
$\begin{align}
56 &= 8 \times 7 \\[1.5ex]
& = (2 \times 4) \times 7 \\[1.5ex]
& = 2 \times (2 \times 2) \times 7 \\[1.5ex]
& = 2 \times 2 \times 2 \times 7
\end{align}$
$\begin{align}
20 & = 4 \times 5 \\[1.5ex]
& = (2 \times 2) \times 5 \\[1.5ex]
& = 2 \times 2 \times 5
\end{align}$
よって、[1]は次のように書けます。
$\dfrac{20}{56} = \dfrac{2 \times 2 \times 5}{2 \times 2 \times 2 \times 7}$
続いて[2]の分数です。分母:75、分子:35なので、この2つを素因数分解します。
$\begin{align}
75 & = 15 \times 5 \hspace{13pt} (75 \div 5 = 15) \\[1.5ex]
& = (3 \times 5) \times 5 \\[1.5ex]
& = 3 \times 5 \times 5
\end{align}$
$35 = 5 \times 7$
よって、[2]は次のように書けます。
$\dfrac{35}{75} = \dfrac{5 \times 7}{3 \times 5 \times 5}$
ステップ2:約分
次に、分母と分子は同じ数で割ってもよいということを利用して、分数を簡単な形にします。そのために、分母と分子を共通している因数で割ります。これがいわゆる約分(やくぶん)です。
[1]の場合、$2 \times 2 = 4$の部分が共通しているので、分母と分子を4で割ります。
$\begin{align}
& \hspace{13pt} \dfrac{20}{56} \\[1.5ex]
& = \dfrac{(2 \times 2 \times 5) \div 4}{(2 \times 2 \times 2 \times 7) \div 4} \\[1.5ex]
& = \dfrac{5}{2 \times 7} (= \dfrac{5}{14})
\end{align}$
[2]の場合、5が共通しているので、分母と分子を5で割ります。
$\begin{align}
& \hspace{13pt} \dfrac{35}{75} \\[1.5ex]
& = \dfrac{(5 \times 7) \div 5}{(3 \times 5 \times 5) \div 5} \\[1.5ex]
& = \dfrac{7}{3 \times 5}(= \dfrac{7}{15})
\end{align}$
ちなみに、次の操作(通分)に備え、まだ分母は計算せずに素因数分解されたままにしておくことをオススメします。
ステップ3:通分
分数を簡単な形にしましたが、これではまだ比べることができません。
ではどうしたら比べることができるのかというと、分母をそろえる必要があります。
わかりやすいように一度簡単な割り算に戻って考えてみましょう。次の2つを比べた時、どちらの方が答え(商)が大きいでしょうか?
(1) 12個のアメを3人に配る($12 \div 3$)
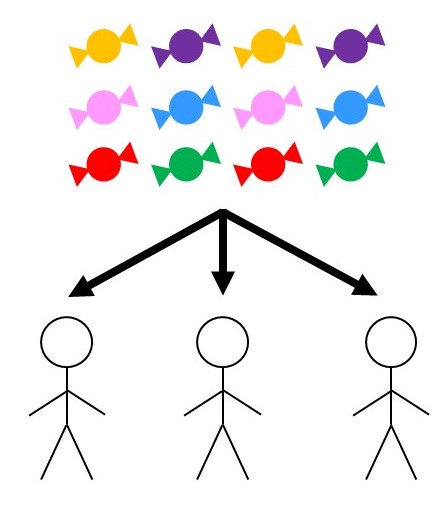
(2) 18個のアメを3人に配る($18 \div 3$)
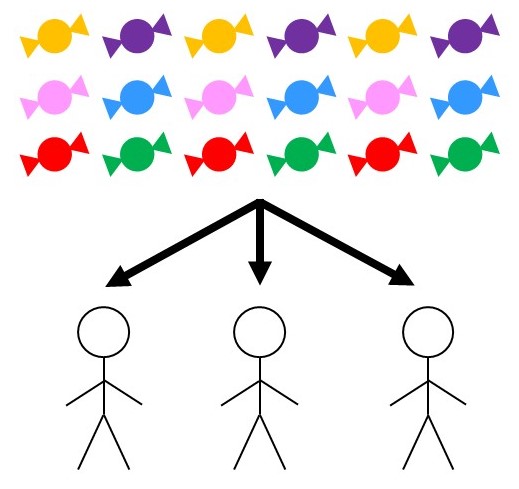
計算すればもちろん➁であることがわかりますが、比べるだけなら計算しなくてもわかります。なぜなら、同じ人数で割るのであればアメの個数が多い方が当然1人分の数も多くなるからです。
つまり、割り算では「割る数が同じ→割られる数が大きい方が答え(商)も大きい」ということであり、割り算を書き換えた分数では「分母が同じ→分子が大きい方が分数も大きい」と言えるわけです。
それでは「分母をそろえる操作」である通分(つうぶん)を行ってみましょう。
通分するには、分母を見比べて足りないものを補うようにするのがコツです。まずは2つの分数をよく見てみましょう。
[1] $\dfrac{5}{2 \times 7}$ [2] $\dfrac{7}{3 \times 5}$
[1]の分母には[2]の分母にある3と5が、[2]の分母には[1]の分母にある2と7がありません。そこで、[1]では分母と分子に15(=3×5)を、[2]では分母と分子に14(=2×7)を掛けます。
[1] $\dfrac{5 \times 15}{2 \times 7 \times 15} = \dfrac{75}{210}$
[2] $\dfrac{7 \times 14}{3 \times 5 \times 14} = \dfrac{98}{210}$
これで分母がそろったので、あとは分子同士を比べれば大小が分かります。[2]の方が大きいですね。
トピック 倍数(素因数)の見分け方
素因数分解を行う際、「どんな数の倍数なのか(どんな数を素因数に持つのか)」見分けることができれば楽ができます。その見分け方でよく知られているものを紹介します。
2の倍数
ある数が2の倍数である場合、下1桁の数が0, 2, 4, 6, 8のいずれかになります。いわゆる偶数と呼ばれる数のことですね(反対に2の倍数でないものは奇数と呼ばれます)。
(例)$38 \div 2 = 19$なので、38は2の倍数(2を素因数に持つ)。
3の倍数
ある数が3の倍数である場合、各位の数を足した時の数が3の倍数になります。
(例)123は$1 + 2 + 3 = 6$であり、6は3の倍数($6 = 3 \times2$)なので、123は3の倍数(3を素因数に持つ)。
5の倍数
ある数が5の倍数である場合、下1桁の数が0, 5のいずれかになります。
(例)$335 \div 5 = 67$なので、335は5の倍数(5を素因数に持つ)。
まとめ
今回は分数の大小を比べる方法として、素因数分解と約分・通分について学びました。良い機会だったので、用語もたくさん紹介しましたが、簡単にまとめると次のようになります。
<分数の大小を比べる方法>
- 分母と分子について素因数分解を行う
- 約分して分数を簡単な形にする(分母は素因数分解されたままにしておく)
- 通分して分母をそろえ、分子の大小から分数の大小を判断する
学校で約分と通分を初めて学ぶ時、約数や倍数の話は出てくるかもしれませんが、おそらく素因数分解の話はまだ出てこないかと思います。
ですが、まてがめが思うに、素因数分解を知っていた方が分数はかなり扱いやすいです。特に今回学んだ約分と通分を行う時には大きな力を発揮します。
素因数分解については、この後√(ルート)を学ぶ時にもお世話になります。慣れるという意味でも、自分でいろんな数を素因数分解して遊んでみてください(高尚な遊び…笑)。
約分と通分を学んだことで分数の計算を学ぶための準備もできました。次回からはそこを学んでいきましょう。
長くなりましたが今回はここまでです。お疲れさまでした!