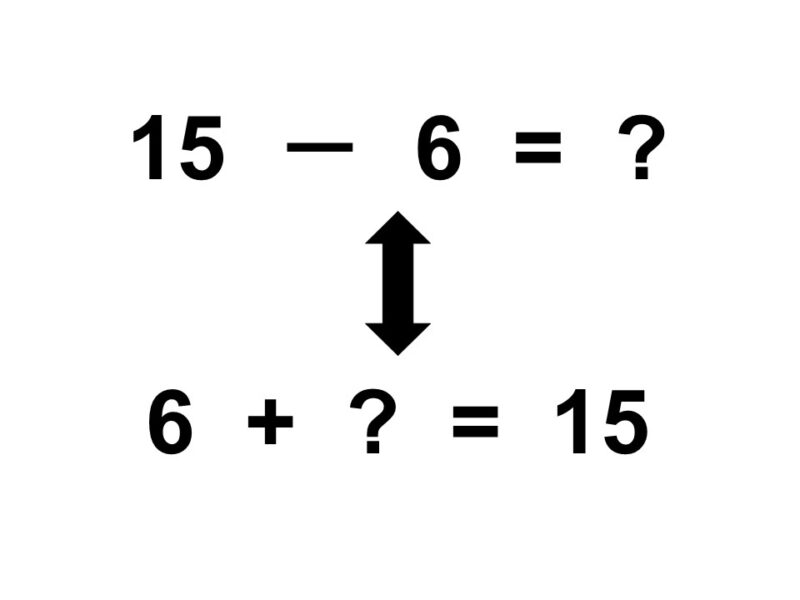こんにちは、まてがめです。
ここまで2階にわたり「足し算」について学んできました。
足し算は「数を数える」という考え方の延長にあり、計算すると数は足す前よりも大きくなります。しかし、数を数えるのはモノが増えるような時だけではありません。例えば、モノを消費した時にも数は数えますよね?
つまり「数が小さくなる」ような計算もあっていいはずです。それが今回学ぶ引き算になります。
引き算(減法)とは?
さっそく具体例から見てみましょう。
卵を使ってケーキを作ることにした。冷蔵庫には卵が7個あったので、そのうち5個使った。
この時、卵は何個残るか?
まずは基本である「数を数える」ところから考えてみましょう。
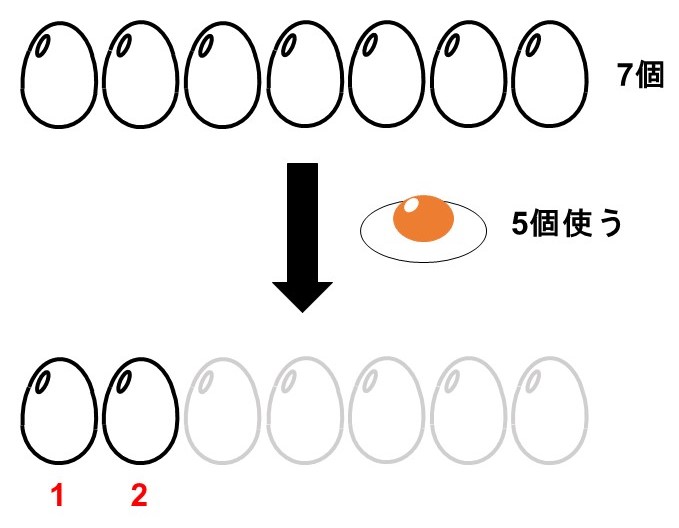
答えは2個ですね。
このような状況は引き算(減法ともいいます)として表すことができます。すなわち、引き算を表す記号-を使うと、次のような等式が書けます。
$7-5 = 2$
また、引き算の答えを差(さ)と呼びます。
言葉の通り、足し算は「数を足し合わせる」計算であるのに対して、引き算は「数を差し引く」計算なので、2つはいわば真逆の関係にあります。
引き算ができる=足し算ができる
足し算について学んだときは「9+9までの足し算は覚えるくらいに慣れておいた方がいい」と言いましたが、18(=9+9)より小さい数同士の引き算については覚えなくても大丈夫です。なぜなら、足し算に慣れていれば、引き算の答え(差)が自然とわかるからです。
次の引き算はわかりますか?
$15-6 = \text{?}$
数を数えても答えが出せますが、足し算が身についていると簡単に答えが出せます。引き算は足し算の逆なので、「15になるためには6と何を足せばよいか?」を考えれば、それが答えになります。
$15-6 = \text{?}$ ⇔ $6 + \text{?} = 15$
$6 + 9 = 15$なので、
$15-6 = 9$
となります。
足し算に慣れることは、引き算を得意にするための近道ですよ。
0の入った引き算は?
足し算の時と同様に、引き算で0がどう扱われるかも見ておきましょう。
(1) 数から0を引く場合
これは卵を使わなかった場合になりますから、
$7-0=7$
となります。
(2) 0から数を引く場合
卵がなければ卵を使うことはできないので、
$0-5$
という式は今回計算できません。(現実を超越してしまいます…)
ただし、状況によっては計算することができるのですが、それについてはまた別の機会でお話ししましょう。
ひとまずここでは、数から0を引いても数は変わらないが、0から数を引くことはできないということにしておきます。
複数の引き算
引き算の場合も、数を差し引くのが1回だけということはありません。次のような例を考えてみましょう。
冷蔵庫には卵が7個あり、ケーキを作るのに5個使った後、目玉焼きを作るのに1個使った。
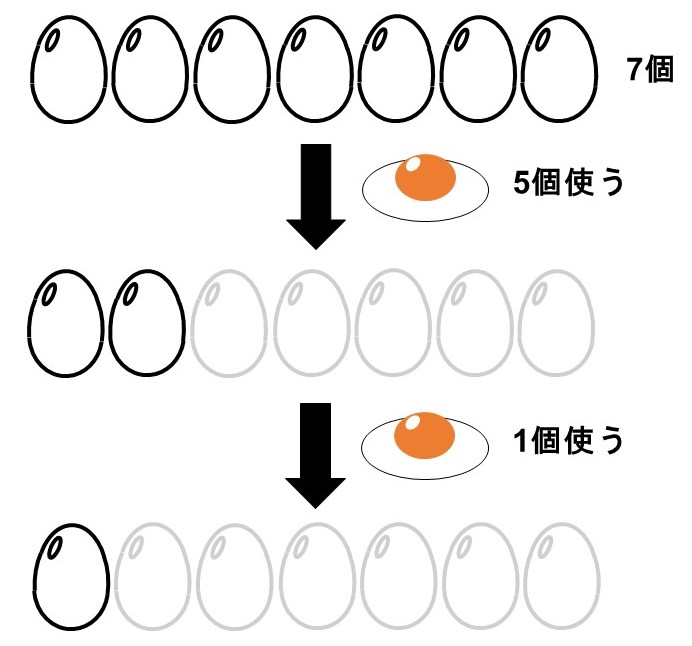
この時、残りの卵は何個になるか?
もはや数えた方が早そうですが、今回は計算から求めてみましょう。式にすると、
$7-5-1$
$7-5 = 2$なので、
$7-5-1 = 2-1$
$2-1 = 1$なので、
$\begin{align}
7-5-1 & = 2-1 \\[1.5ex]
& = 1
\end{align}$
よって、答えは1個ですね。
ちなみに、足し算の時と同じように順番を入れ替えて計算することもできます。
$\begin{align}
7-5-1 & = 7-1-5 \\[1.5ex]
& = 6-5 \\[1.5ex]
& = 1
\end{align}$
足し算と引き算が一緒に出てきたときは?
足し算と引き算が同時に出てくることもあります。次のような例です。
冷蔵庫には卵が7個あり、ケーキを作るのに5個使ったが、お父さんが4個買ってきてくれた。
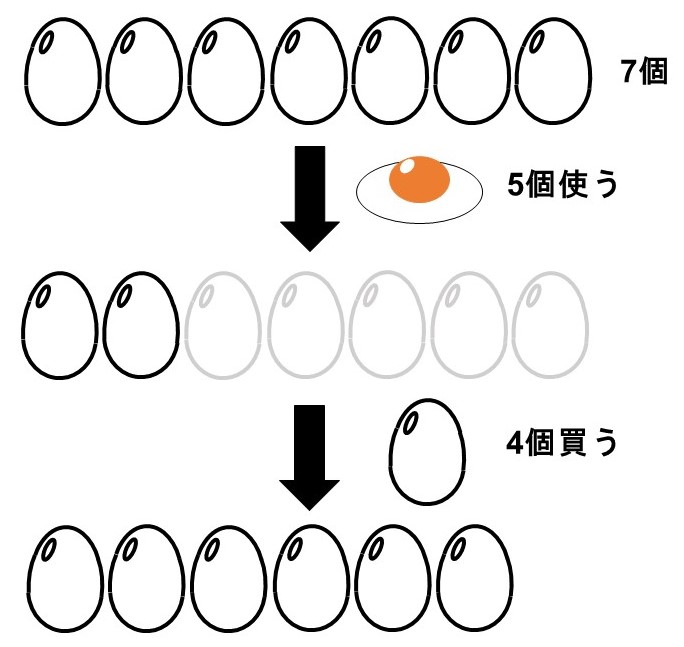
この時、残りは何個になるか?
式にすると、
$7-5 + 4$
とりあえず前から計算していきます。$7-5 = 2$なので、
$7-5 + 4 = 2 + 4$
$2 + 4 = 6$なので、
$\begin{align}
7-5 + 4 & = 2 + 4\\
& = 6
\end{align}$
よって、答えは6個です。どうやらこの家族は卵が好きなようですね。
次のように順番を入れ替えて計算することもできます。
$\begin{align}
7-5 + 4 & = 7 + 4-5 \\[1.5ex]
& = 11-5 \\[1.5ex]
& = 6
\end{align}$
まとめ
今回は引き算(減法)について学びました。簡単にまとめておきます。
- 引き算は足し算の逆 → 足し算から考えれば答えがわかる
- 数から0を引いても数は変わらないが、0から数を引くことはできない(※状況による)
- 足し算と同じように、引き算も順番を入れ替えて計算できる
引き算は足し算とは異なる新しい計算方法ではなく、足し算と真逆の計算であり、ゆえに足し算から逆算できるという考え方がとても大切です(実は方程式を学ぶ時にも活きてきます)。
今回はここまでです。お疲れさまでした!