こんにちは、まてがめです。
これまでに基礎となる4つの計算方法「足し算(加法)」、「引き算(減法)」、「掛け算(乗法)」、「割り算(除法)」について学んできました。これらはまとめて四則演算(しそくえんざん)と呼ばれます。
数を別の数に変換するための特別なルール(いわゆる三角関数、指数関数、対数関数など)を除けば、計算を行う際には通常この4つが組み合わさった形でしか出てきません。なので、これらさえを身につけていれば、基本的にすべての計算が理解できるはずです。
計算は数学を学ぶための基礎です。上の階へ行くためにも、ここでしっかり復習しておきましょう!
足し算(加法)
足し算(加法)とは?
足し算(加法)は、数に数を足し合わせる操作です。+という記号で表し、その答えを和と呼びます。
(例)
$7 + 3 = 10$
足し算は数を数えることで答え(和)を求めることができます。しかし足し算のメリットは、9+9までの基本的な足し算を覚えておくことで、全ての足し算において「実際に数えなくても数がわかる」という点にあります。
なので、9+9までの足し算については覚えるようにしましょう。
詳しい解説はこちら↓
足し算における筆算
筆算は大きな数の足し算に便利です。筆算を行う時は「位をそろえて縦に計算すること」、「繰り上がり」に注意にしましょう。
(例)
$2374 + 328 = 2702$
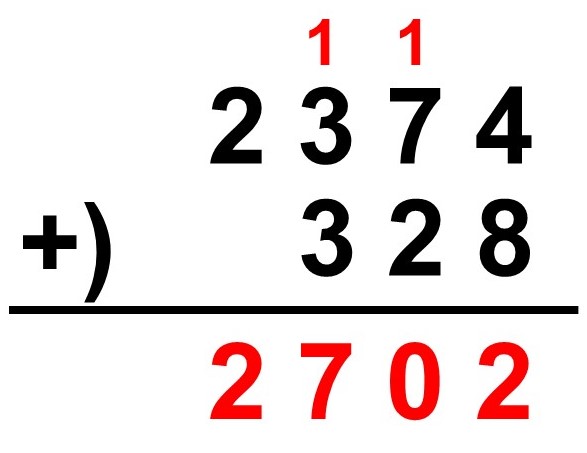
詳しい解説はこちら↓
引き算(減法)
引き算(減法)とは?
引き算(減法)は、数から数を差し引く操作です。-という記号で表し、その答えを差と呼びます。
(例)
$8-5 = 3$
引き算は足し算と逆の操作になるので、足し算に戻って考えれば自然と答えが分かります。
$8-5 = \textbf{3}$ ⇔ $\textbf{3} + 5 = 8$
詳しい解説はこちら↓
引き算における筆算
足し算と同じように引き算においても、大きな数を計算する時は筆算が便利です。足し算では「繰り上がり」が起こりますが、引き算では「繰り下がり」に気をつけましょう。
(例)
$3592-1393 = 2199$
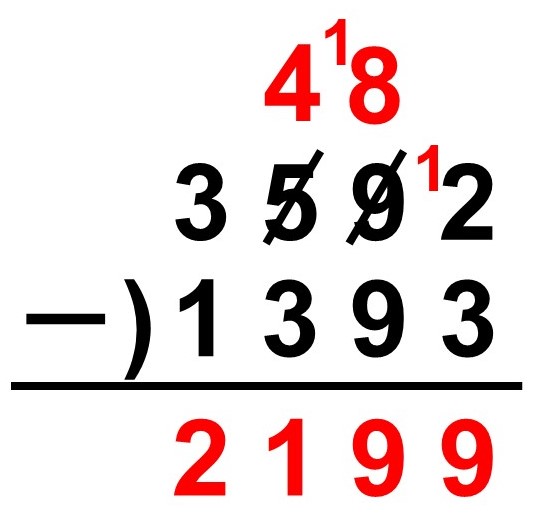
詳しい解説はこちら↓
掛け算(乗法)
掛け算(乗法)とは?
掛け算(乗法)は、数に数を掛ける操作です。×という記号で表し、その答えを積と呼びます。
(例)
$3 \times 7 = 21$
掛け算のメリットは「足し算をシンプルな形で表せること」、「一見複雑に見える問題を単純な計算で表せること」です。つまり、物事をシンプルに見るための道具として使えるということです。
なので、掛け算そのものを計算するのに時間がかかっていては、掛け算を上手く扱えていないことになってしまいます。9×9までの掛け算は覚えておいて、すぐに使えるようにしておきましょう。
詳しい解説はこちら↓
掛け算における筆算
掛け算の筆算は足し算や引き算に比べると少し複雑ですが、やっていることは分配法則(後ほど解説)から導かれる計算にすぎません。計算する順番や位の位置に気をつけましょう。
(例)
$358 \times 23 = 8234$
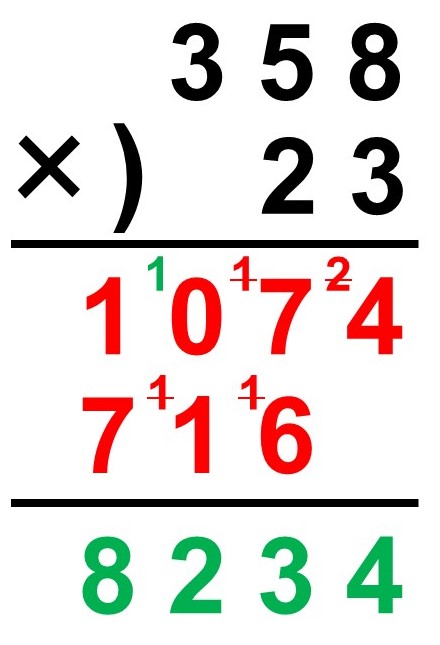
※分配法則を使って計算すると次のようになります。
$\begin{align}
& \hspace{13pt} 358 \times 33 \\[1.5ex]
& = 358 \times (30 + 3) \\[1.5ex]
& = 358 \times 30 + 358 \times 3 \\[1.5ex]
& = (300 + 50 + 8) \times 30 + (300 + 50 + 8) \times 3 \\[1.5ex]
& = 300 \times 30 + 50 \times 30 + 8 \times 30 + 300 \times 3 + 50 \times 3 + 8 \times 3 \\[1.5ex]
& = 9000 + 1500 + 240 + 900 + 150 + 24 \\[1.5ex]
& = 11814
\end{align}$
詳しい解説はこちら↓
割り算(除法)
割り算(除法)とは?
「割り算(除法)」は、数を数で割る操作です。÷という記号で表し、その答えを商と呼びます。
(例)
$32 \div 4 = 8$
割り算は掛け算の逆の操作になるので、掛け算に戻って考えると計算しやすいです。
$32 \div 4 = \textbf{8}$ ⇔ $\textbf{8} \times 4 = 32$
また、割り切れずに余り(剰余)が出てしまう場合は、素直にそのことを書きましょう。
$64 \div 9 = 7 \hspace{2pt} \text{…} \hspace{2pt} 1$
(⇔ $7 \times 9 + 1 = 64$)
詳しい解説はこちら↓
割り算における筆算
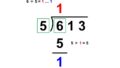
割り算における筆算では、他の計算方法とは異なり、大きい位から順番に答え(商)を決めていきます。
(例)
$38652 \div 19 = 2034 \hspace{2pt} \text{…} \hspace{2pt} 6$
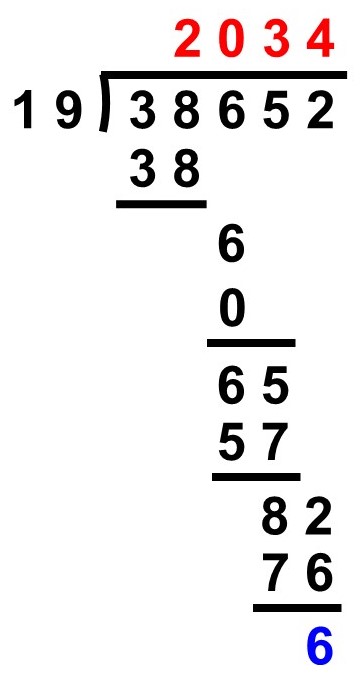
詳しい解説はこちら↓
四則演算を行う時のポイント
加減乗除が混ざった時の計算は、「何ができて何ができないのか」を理解していないと上手く計算できません。特に重要なものを確認しておきましょう。
計算の優先順位は「カッコの中 → 掛け算・割り算 → 足し算・引き算」
ちなみにカッコの中で加減乗除が混ざっていた場合は、その中で同じルールが適用されます。
(例)
$\begin{align}
&\hspace{13pt} (64 \div8 + 10) \times 2-3 \\[1.5ex]
&= (8+10) \times 2-3 \\[1.5ex]
& =18 \times 2-3 \\[1.5ex]
& = 36-3 \\[1.5ex]
& = 33
\end{align}$
足し算・引き算同士で「位置を入れ替えたり、計算のタイミングを変えたりできる」
ただし現時点で(小さい数)-(大きい数)はできないので、そのような形になることだけは避けておきましょう。
次の例では、区切りの良い数が作れるように計算を工夫しています。
(例1)
$\begin{align}
& \hspace{13pt} 58-13 + 26 + 42 \\[1.5ex]
& = 58 + 42 + 26-13 \\[1.5ex]
& =\textbf{100} + \textbf{13} \\[1.5ex]
& = 113
\end{align}$
カッコ・掛け算・割り算がある場合は、計算の順番を優先してください。
(例2)
$\begin{align}
& \hspace{13pt} 5 \times 3 + 7 + (13-4) \div3 \\[1.5ex]
& = 5 \times 3 + 7 + 9 \div 3 \\[1.5ex]
& = 15 + 7 + 3 \\[1.5ex]
& = 15 + 10 \\[1.5ex]
& = 25
\end{align}$
掛け算同士で「位置を入れ替えたり、計算のタイミングを変えたりできる」
複数の掛け算が出てきたときは、区切りの良い数を作ると早く計算できます。
(例)
$\begin{align}
& \hspace{13pt} 2 \times 3 \times 4 \times 5 \\[1.5ex]
& = 2 \times 5 \times 3 \times 4 \\[1.5ex]
& = \textbf{10} \times 12 \\[1.5ex]
& = 120
\end{align}$
同じ数の掛け算・割り算には分配法則が使える
同じ数の掛け算や割り算が散らばっている時はまとめることができます。
(例1)
$\begin{align}
& \hspace{13pt} 6 \times 23-6 \times 18 \\[1.5ex]
& = 6 \times (23-18) \\[1.5ex]
& = 6 \times 5 \\[1.5ex]
& = 30
\end{align}$
(例2)
$\begin{align}
& \hspace{13pt} 11 \div 6 + 13 \div 6 \\[1.5ex]
& = (11 + 13) \div 6 \\[1.5ex]
& = 24 \div 6 \\[1.5ex]
& = 4
\end{align}$
詳しくはこちら↓
練習問題
これまでの内容が理解できているか確認するために、次の練習問題を解いてみましょう。
Aさんはお店で1袋8枚入りのせんべい(198円)を3袋、1袋24個入りのチョコ(285円)を2袋買った。
買ってきたお菓子は家に遊びに来ていた友達のBさん、Cさん、Dさんの計4人で分けることにしたが、Cさんはチョコが苦手だったため、Cさんにはチョコを分けない代わりにせんべいを予定よりも2枚多くあげることにした。
友達の3人が帰った後、余ったお菓子は後で食べようと明日にとっておくことにした。
【問題】
(1) Aさんはお店にいくらお金を払ったか?
(2) Bさんに分けたせんべいとチョコはそれぞれいくつか?
(3) 余ったお菓子は何か?またいくつ余ったか?
(4) 余ったお菓子を見つけた弟が自分も食べたいと言ってきた。どうしたらよいか?
まずは答えを見ないで、自分で考えてみてください。
答えはこちら↓
【解答】
(1)
$\begin{align}
& \hspace{13pt} 198 \times 3 + 285 \times 2 \\[1.5ex]
& = 594 + 570 \\[1.5ex]
& = 1164
\end{align}$
よって、払ったお金は1164円。
(2)
せんべいについて考える。せんべいの枚数は$8 \times 3 = 24$なので、4人で分けた場合は
$24 \div 4 = 6$
つまり、6枚ずつ食べることになる。
ただし、今回はCさんに2枚多くあげることになったので、先にCさんにせんべいを分けておくと
$24-(6 + 2) = 16$
つまり、残り16枚をAさん、Bさん、Dさんの3人で分けることになる。
$16 \div 3 = 5 \hspace{2pt} \text{…} \hspace{2pt} 1$
よって、Bさんに分けたせんべいは5枚(1枚余り)。
次にチョコについて考える。チョコの個数は$24 \times 2 = 48$なので、Cさん以外の3人で分けた場合は
$48 \div 3 = 16$
よって、Bさんに分けたチョコは16個。
(3) (2)から、余ったお菓子はせんべいであり、余ったのは1枚。
(4) 2通りの答えが考えられる。
- 余ったせんべいを弟にあげる。
- 余ったせんべいを2人で分ける。
全て計算できたでしょうか?
最後の問題の答えについては、余ったのがせんべい1枚ですし、Aさんはすでに5枚も食べているので、弟にあげるのが普通ですね(チョコも16個は食べ過ぎ 笑)。
…という話はひとまず置いておいて、残った1枚を2人で分けるという場合についても考えてみましょう。
この場合の1人分はどう数えたらよいのでしょうか?半分にするので、もはや1枚と数えることはできません。
実はこれを解決してくれるのが、これから学ぶ分数・小数と呼ばれるものです。
まとめ
四則演算は数学を学ぶための基礎ですが、基礎というのは「土台」という意味であって、決して「簡単」という意味ではありません。
いろいろな計算を経験することで、少しずつ自分の間違えやすいポイントに気がつき、式に応じた工夫ができるようになるものです。
今回で四則演算の内容は終わりですが、自分でトレーニングしたり、新しい内容で出てくる計算を自分で解いたりするなど、アウトプットを大切にして力をつけていってくださいね。
今回はここまでです。次の階でまたお会いしましょう!