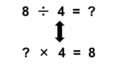こんにちは、まてがめです。
前回は4つ目の計算方法である「割り算」について学びました。足し算と引き算が対になっているように、掛け算と割り算も対になっているというのが重要なポイントでしたね。
今回は2桁以上の大きな数の割り算で使う筆算を学んでいきます。実はこれまでの筆算とは大きく異なるポイントがあります。それは「大きな位から数を決めていく」という点です。
割り算における筆算
パターン1:割り切れる場合
いつものように具体例を考えてみます。
5236人の来場者を、人数の等しい17個のグループに分けて会場へ入場させたい。
この時、1グループあたりの人数はいくつになるか?
式は次のようになります。
$5236 \div 17$
もしこの計算が割り切れる(余りが出ない)のであれば、「求める人数が17グループ集まると5236人になる」ということですから、次の式の「?」が知りたいということですね。
$\text{?} \times 17=5236$
この割り算を今まで学んだことだけで挑もうとすると、「17と掛け算をした時に5236になる数をひたすら探す」という面倒な作業をしなくてはなりません(工夫すればできないこともありませんが…)。
楽をするのであれば、やはり一発で答えを求めたいところです。そこで、筆算を使います。
割り算で筆算を行う場合は次のような形で準備します。

割り算における筆算は今までとは形が全く違いますが、これは筆算のやり方が違うからです。
すなわち、足し算、引き算、掛け算における筆算は「小さい位から順に大きい位へと計算していく方法」であったのに対して、割り算における筆算は「大きな位から順に小さい位へと計算していく方法」であるという違いがあります。
この後計算してみるとわかりますが、こうした違いは、足し算、引き算、掛け算では「繰り上がり」や「繰り下がり」を工夫して使うのに対し、割り算では「余り」を工夫して使うことに由来しています。
<筆算の方法>
- 足し算、引き算、掛け算:小さい位 → 大きい位へと計算
- 割り算:大きい位 → 小さい位へと計算
このことを意識してさっそく計算してみましょう。
割られる数(今回は5236)の上に割り算の結果(商)を書いていくのですが、大きな位から順に商がいくつになるかを調べていきます。
(1) 千の位を調べる
〔割られる数の上1桁(5)〕÷〔割る数(17)〕が計算できるか確認します。もちろん5÷17はできません。
このことは、商が1000よりも小さい(千の位がない)ことを意味しています。
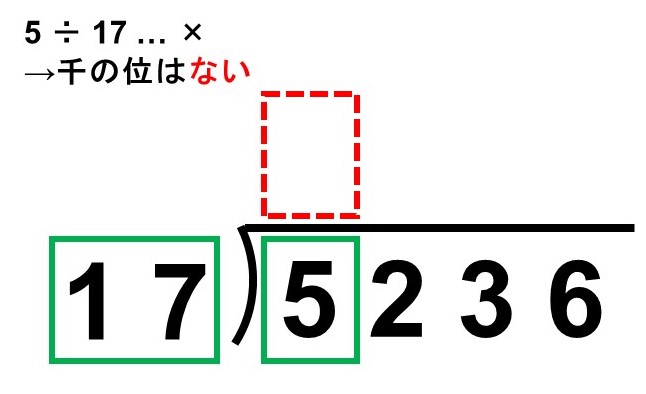
(2) 百の位を調べる
今度は〔割られる数の上2桁(52)〕÷〔割る数(17)〕が計算できるか確認します。
$52 \div 17 = 3 \hspace{2pt} \text{…} \hspace{2pt} 1$
余りは出ますが計算できますね。そうしたら、計算結果である3を百の位として書きます。
一方、$17 \times 3=51$なので、51は52の下に書いてそのまま引き算を行います。ここで出てくる1は余りのことですね。
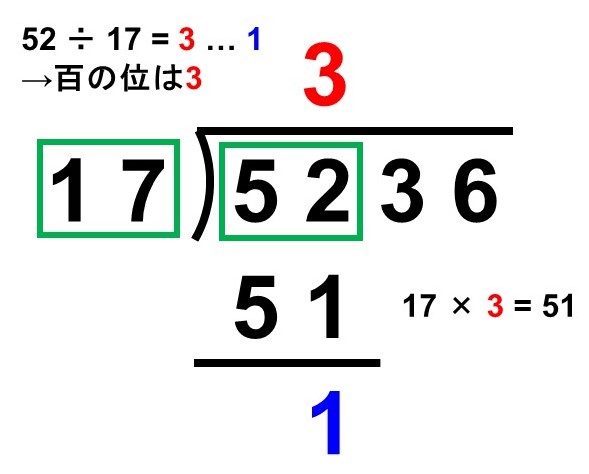
ここまでの操作で、商の百の位は3であることがわかりました。
(3) 十の位を調べる
余りが出たので、割られる数の十の位(3)を下ろし、13とします。
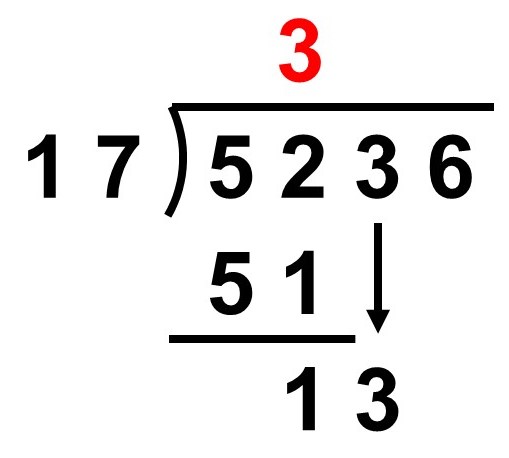
続いて、13÷〔割る数(17)〕が計算できるか確認します。当然できないので、0を十の位として書きます。一方、$17 \times 0 = 0$なので、0は13の下に書いてそのまま引き算を行います。
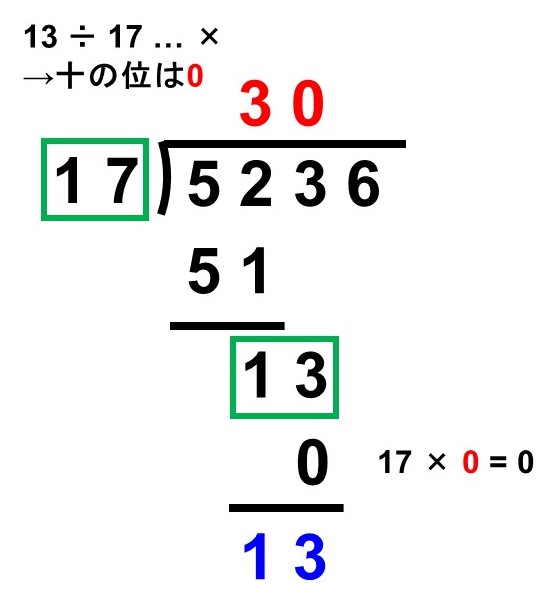
ここまでの操作により、商の十の位は0であることがわかりました。
(4) 一の位を調べる
割られる数の一の位(6)を下ろし、136とします。
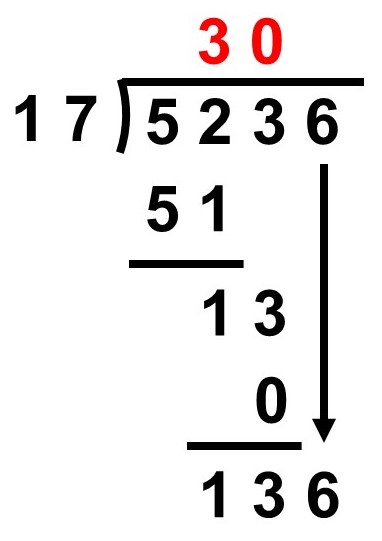
136÷〔割る数(17)〕が計算できるか確認します。
$136 \div 17 = 8$
きれいに割り切れました。そうしたら、8を一の位として書きます。一方、$17\times8=136$なので、136を136の下に書いてそのまま引き算を行います。もちろん余りは0です。
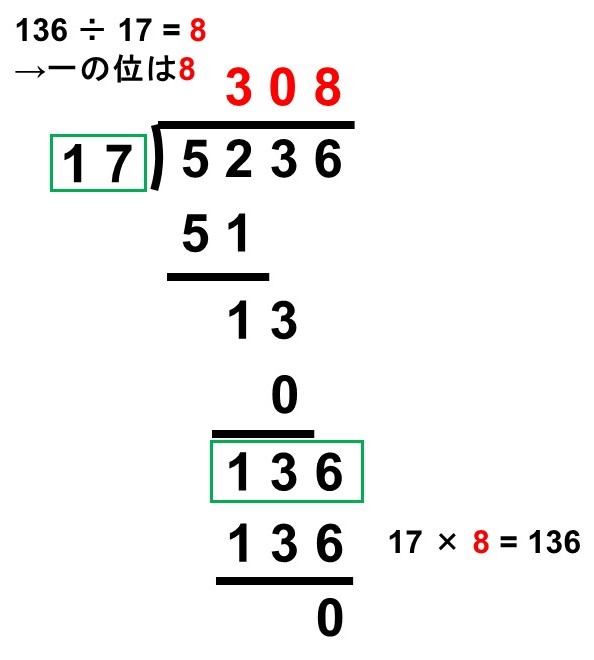
これで計算完了です。商の一の位が8であることがわかったので、計算結果は
$5236 \div 17 = 308$
つまり、308人が答えになります。
筆算のやり方は理解できたでしょうか?このように割り算では、答えである商を求めるのに大きい位から数を調べていきます。この時、余った数は割られる数の下の位と合わせてもう一度考えることで、小さい位の数も決めることができるようになっています。
パターン2:割り切れない場合
復習として、もう一つの例で練習してみましょう。
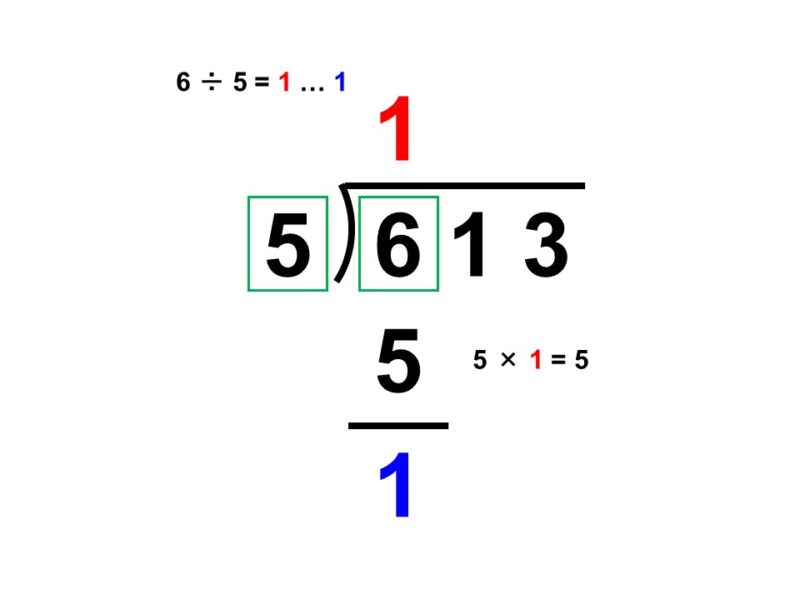
613個のアメがある。これらを子供たち5人に分け、余った分は自分でもらうことにした。
この時、子供たちは1人当たり何個もらえるか?
式は次のようになりますね。
$613 \div 5$
また、筆算は次のように準備します。
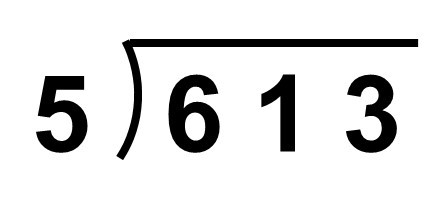
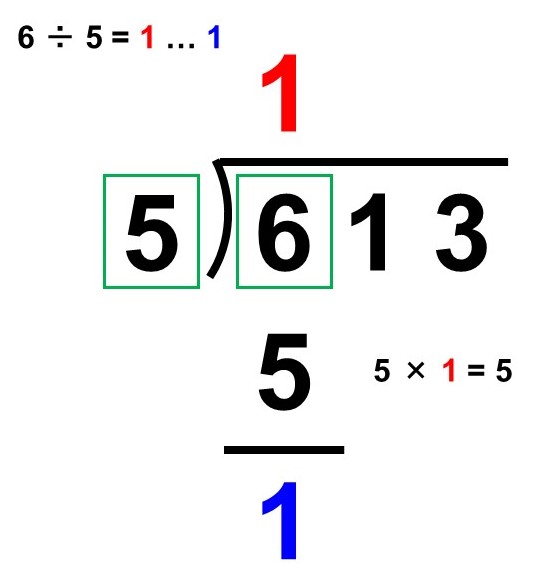
(1) 百の位を調べる
割られる数の百の位(6)について考えると、
$6 \div 5 = 1 \hspace{2pt} \text{…} \hspace{2pt} 1$
よって、商の百の位は1、余りは1です。
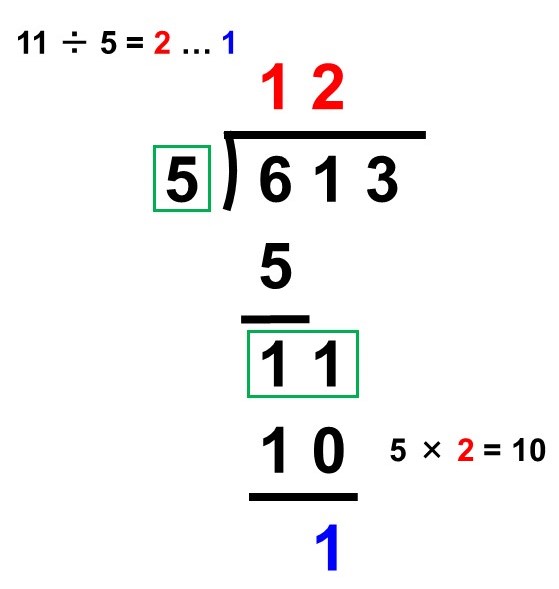
(2) 十の位を調べる
割られる数の十の位(1)を下ろすと11になるので、
$11 \div 5 = 2 \hspace{2pt} \text{…} \hspace{2pt} 1$
よって、商の十の位は2、余りは1です。
(3) 一の位を調べる
割られる数の一の位(3)を下ろすと13になるので、
$13 \div 5 = 2 \hspace{2pt} \text{…} \hspace{2pt} 3$
よって、商の一の位は2、余りは3です。
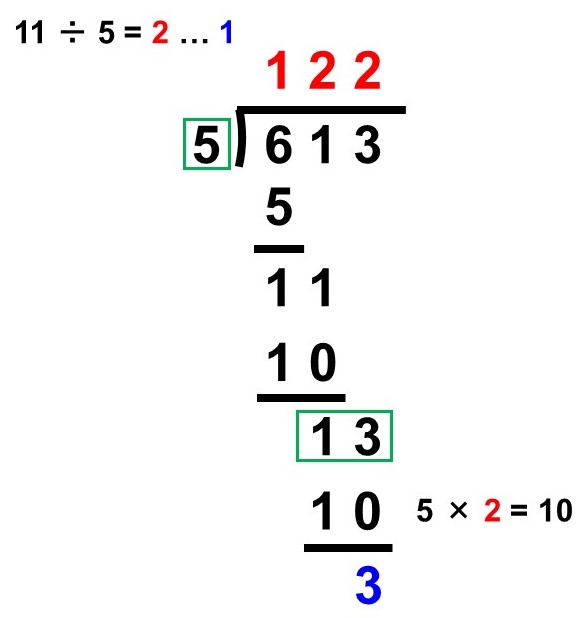
以上から、
$613 \div 5 = 122 \hspace{2pt} \text{…} \hspace{2pt} 3$
となるので、答えは122個です(余りは3個)。
計算できましたか?
まとめ
今回は割り算における筆算について学びました。まとめると次のようになります。
- 割り算の筆算では、大きい位から数を調べる
- 余りが出たら、割られる数の下の位と合わせてもう一度考える
基礎的な計算方法である四則演算については、ここまでで全て学んだことになります。
次の階では、これまでの内容を総復習します。計算は数学の基礎なので、ここで土台を固めてさらに上の階へ行きましょう!
今回はここまでです。お疲れさまでした!