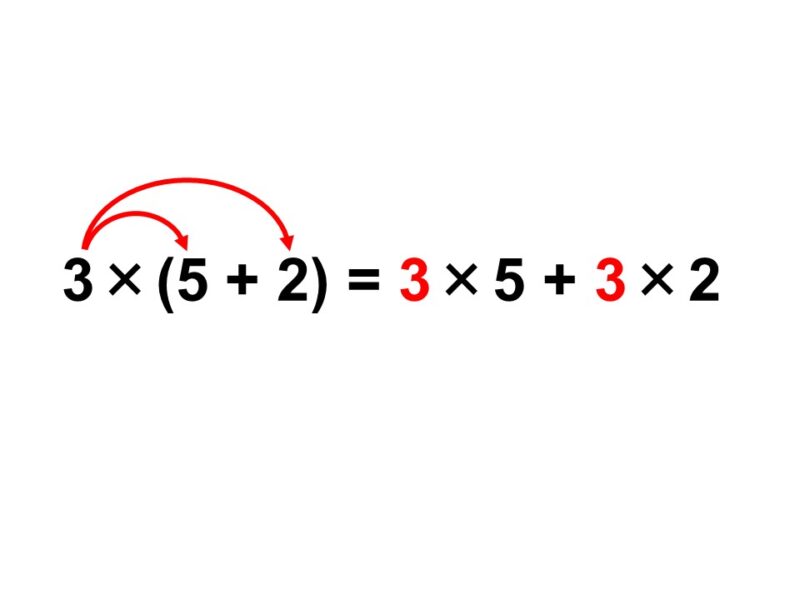7F　計算の順番と分配法則

こんにちは、まてがめです。

前回は3つ目の計算方法として「掛け算」について学びました。使える道具が増えてきましたね。

• 6F　「数を掛け合わせる」 ― 掛け算（乗法）

では、掛け算が足し算や引き算と一緒に出てきた時はどうしたらよいのでしょうか？

実は掛け算が入ってくると、計算の順番を気にする必要が出てきます。

これと合わせて、分配法則（ぶんぱいほうそく）と呼ばれる便利な法則についても学んでいきます。

足し算・引き算・掛け算が混ざった計算 ― 計算の順番と分配法則

パターン1：足し算＆掛け算

次のような例を考えます。

1セット3個入りのテニスボールをお父さんから5セット、お母さんから2セット買ってもらった。

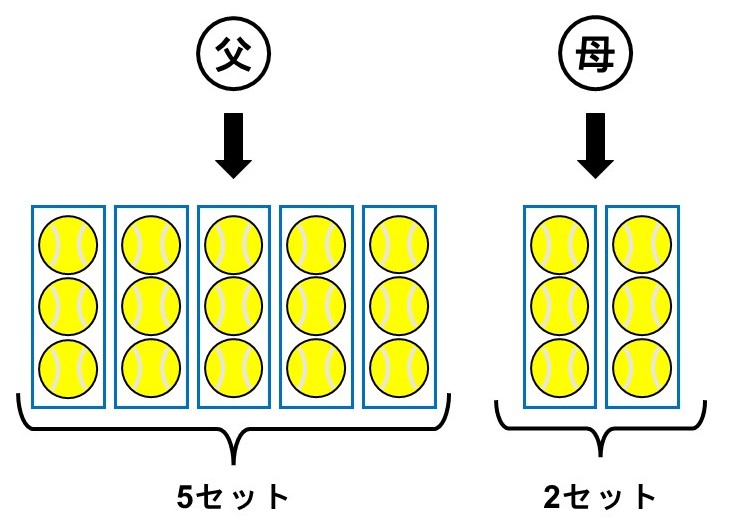
この時、買ってもらったボールは何個になるか？

考え方が2通りあるので、順番に見ていきましょう。

（考え方1）

「お父さんから買ってもらった個数とお母さんから買ってもらった個数をそれぞれ数えてから最後に足し合わせる」と考えてみます。

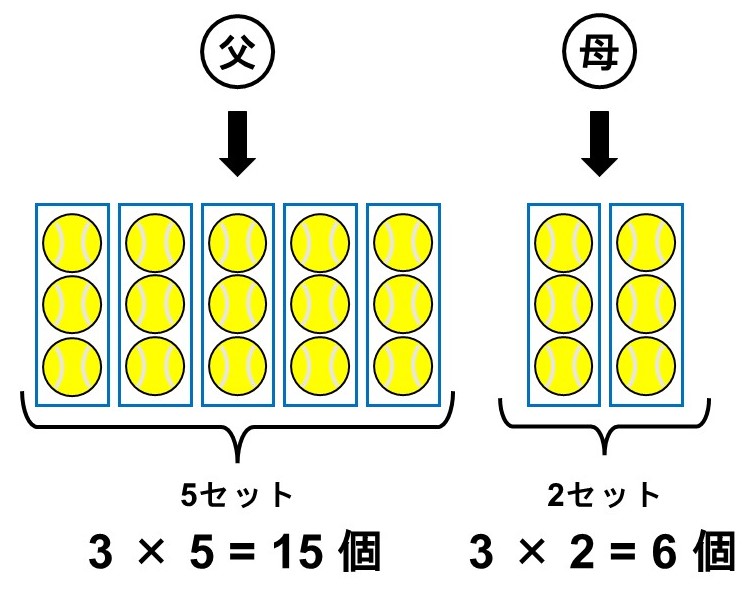
この場合、次のような式を作ることができます。

$3\times5+3\times2$

通常、先に計算したい部分はカッコをつけてわかるようにしておくのですが、今回掛け算の部分にはあえてカッコをつけませんでした。これは計算の優先順位が掛け算 → 足し算と決まっており、カッコを使って優先度を示す必要がないからです。
それでは、計算していきます。

$\begin{align}
3 \times 5 + 3 \times 2 & = 15 + 6 \\[1.5ex]
& = 21
\end{align}$

よって、答えは21個です。

（考え方2）

「全部で何セット買ってもらったのかを確認してからボールの個数を数える」という考え方ではどうでしょうか？

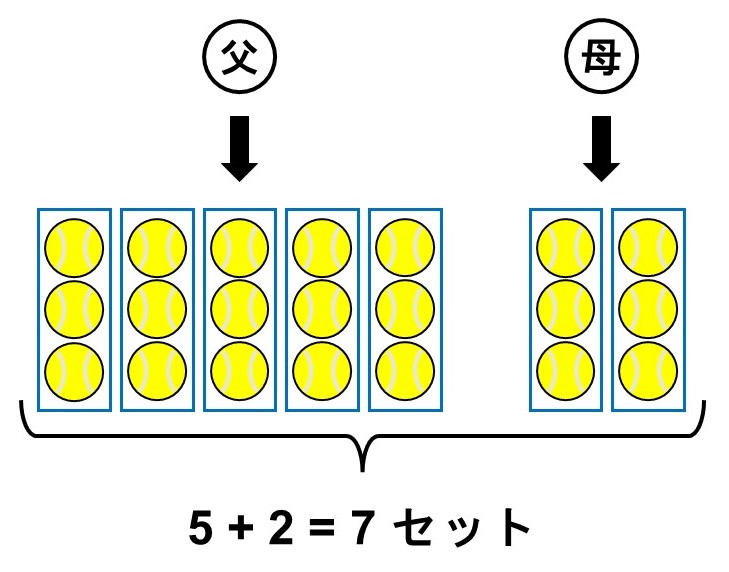
これを式で表すと次のようになります。

$3\times(5+2)$

先ほども言ったように、何も書かなければ掛け算 → 足し算の順で計算が進んでしまうので、足し算を先に計算したい時はカッコをつけて必ずそれがわかるようにします。

$\begin{align}
3 \times (5 + 2) & = 3 \times 7 \\[1.5ex]
& = 21
\end{align}$

こちらも答えは21個になりました。

計算の順番についてはルールなので覚えてしまえばそれで終わりなのですが、もう一つ大切なことがあります。それはこの問題から次の等式が成り立つことがわかったということです。

$3 \times (5 + 2) = 3 \times 5 + 3 \times 2$

これは分配法則（ぶんぱいほうそく）と呼ばれる重要な法則です。この等式で言えば、あたかも3がカッコ内の5と2に分配されて掛け算を行っているように見えるからですね。

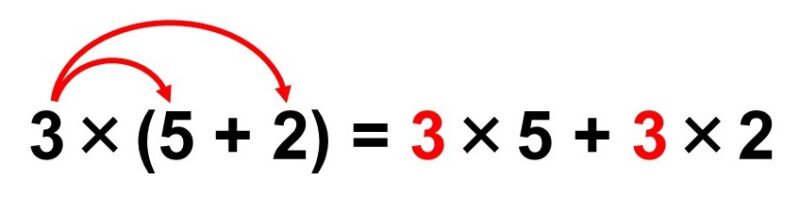
パターン2：引き算＆掛け算

次は少し違う例です。

1セット3個入りのテニスボールをお父さんから7セット買ってもらったが、そのうちの2セットを弟にあげた。

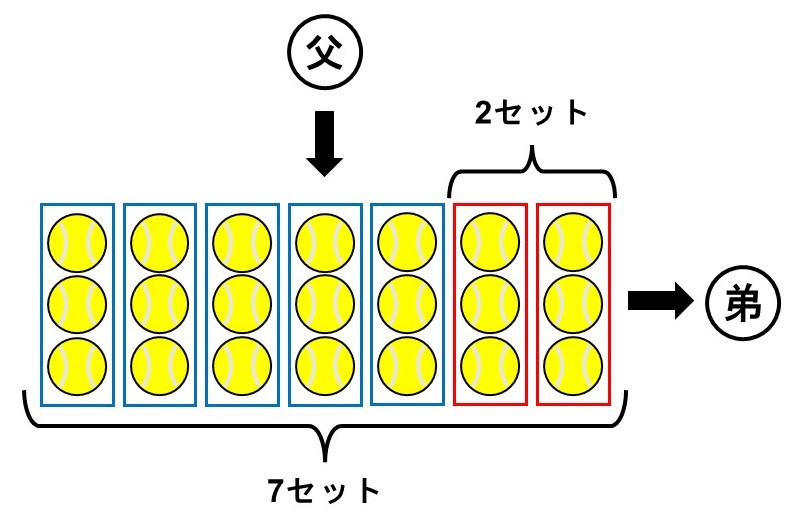
この時、手元に残るボールは何個になるか？

（考え方1）

「お父さんに買ってもらったボールの個数と弟に挙げたボールの個数をそれぞれ数えてから最後に差し引く」と考えてみましょう。

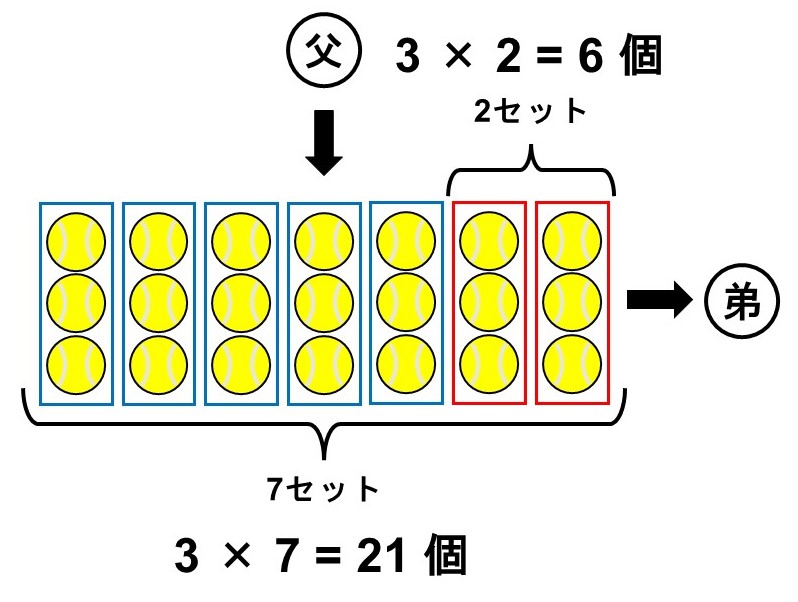
これは次のような式で表せます。

$3 \times 7-3 \times 2$

ここでもカッコは使いません。引き算についても足し算と同様、計算の優先順位は掛け算 → 引き算ということになっているからです。この式を計算すると、

$\begin{align}
3 \times7-3 \times 2 & = 21-6 \\[1.5ex]
& = 15
\end{align}$

よって、答えは15個となります。

（考え方2）

「全部で何セット残っているのかを確認してからボールの数を数える」場合も考えてみましょう。

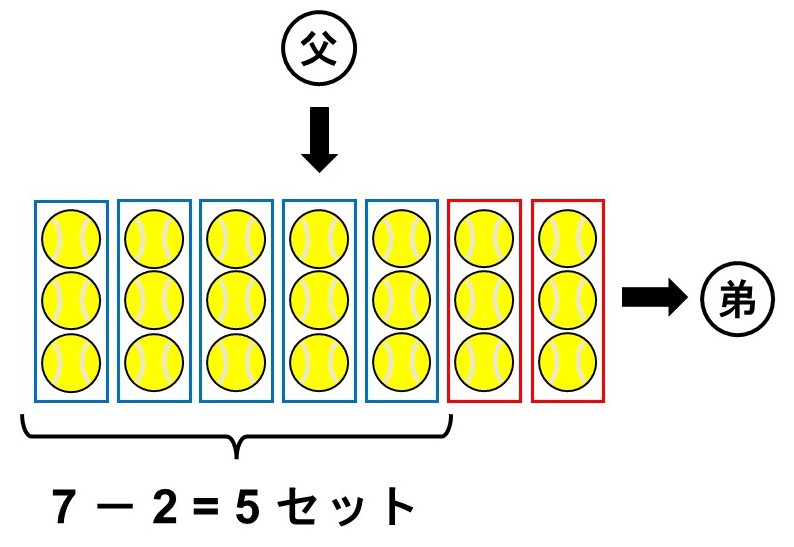
こちらは次のような式になりますね。

$3 \times (7-2)$

やはり何も書かなければ掛け算 → 引き算の順に計算することになるので、ここはカッコを使って引き算が先であることを示しておきます。

$\begin{align}
3 \times (7-2) & = 3 \times 5 \\[1.5ex]
& = 15
\end{align}$

こちらも答えは15個になりました。

このように、分配法則はカッコの中が引き算でも成り立ちます。

$3 \times (7-2) = 3 \times 7-3 \times 2$

分配法則の使い方

先ほど分配法則について説明しましたが、これを上手に使うと色んなことができます。いくつか例を見てみましょう。

ケース1：大きな数の掛け算

次の掛け算を行ってみます。

$5 \times 38$

9×9までの掛け算を覚えているだけでは対応できませんが、分配法則を使うことで次のように計算できます。

$\begin{align}
5 \times 38 & = 5 \times (30 + 8) \\[1.5ex]
& = 5 \times 30 + 5 \times 8 \\[1.5ex]
& = 150 + 40 \\[1.5ex]
& = 190
\end{align}$

大きな数の掛け算については次回お話ししますが、考え方のベースになっているのは分配法則です。

ケース2：逆にカッコでまとめる

ケース1では分配法則の名前通りの使い方でしたが、逆の使い方もできます。次の式を計算してみましょう。

$7 \times 9 + 7 \times 6-7 \times 8$

もちろん掛け算をさばいてから足し算と引き算を行っても答えは出せます。

$\begin{align}
7 \times 9 + 7 \times 6-7 \times 8 & = 63 + 42-56 \\[1.5ex]
& = 105-56 \\[1.5ex]
& = 49
\end{align}$

でもこの場合だと、計算している途中で気づくはずです。「ん？なんか引き算の筆算出てきたぞ（面倒だな…）」

一方で、分配法則を使ったらどうなるでしょうか。

$\begin{align}
7 \times 9 + 7 \times 6-7 \times 8 & = 7 \times (9 + 6-8) \\[1.5ex]
& = 7 \times 7 \\[1.5ex]
& = 49
\end{align}$

こちらの方が見やすい上に計算しやすいように感じませんか？実際、2桁以上の数の計算が全くないですよね。

まとめ

今回は計算の順番と分配法則について学びました。まとめるとこんな感じです。

計算の順番は色んな計算の中で覚えていけば大丈夫です。分配法則は計算を楽にするための道具として使えるので、積極的に使って自分のものにしていきましょう！

今回はここまでです。お疲れさまでした！