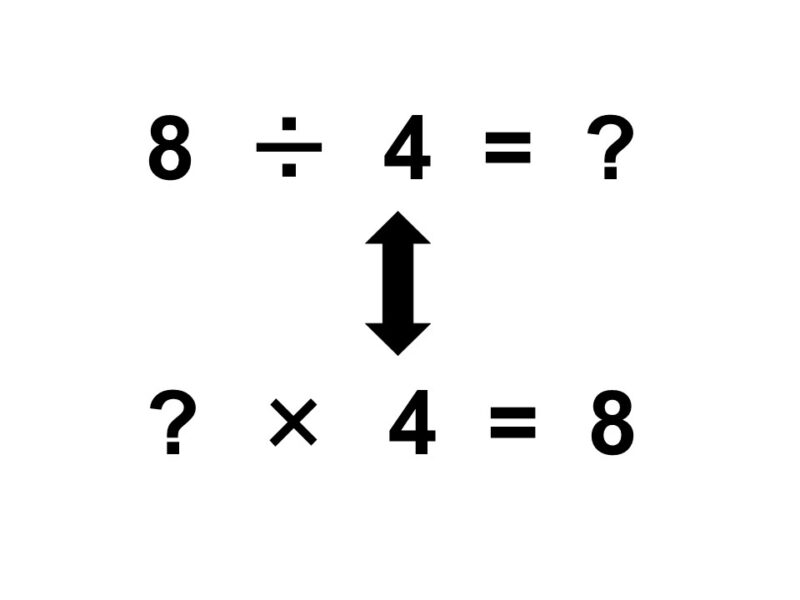こんにちは、まてがめです。
前回までに「足し算」、「引き算」、「掛け算」を学んできました。10進法を学んでいた時から比べれば、みなさんの「数」や「計算」に対する理解は相当深まっているはずです。
今回は四則演算(しそくえんざん)のうち、残る最後の1種類である割り算について学んでいきます。
割り算(除法)とは?
久しぶりにリンゴを使って例を考えます。
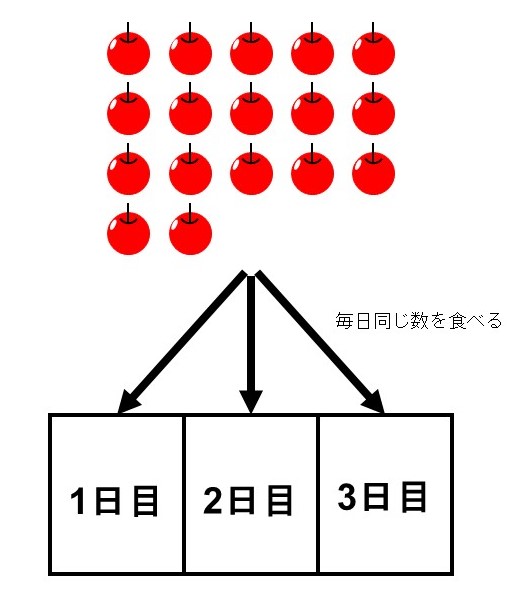
今リンゴが8個あり、これを同じ個数ずつ4日に分けて食べたい。
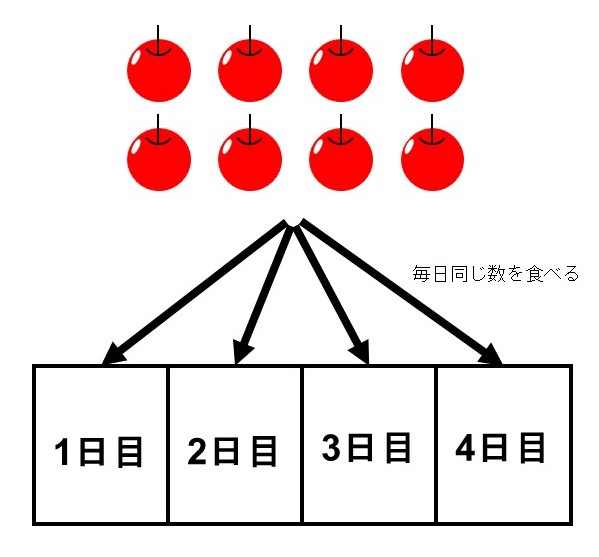
この場合、1日何個食べることになるか?
まずは、これまでに学んだ計算方法から求めることはできないか考えてみます。「同じ数ずつ4日食べる」ということは、今求めようとしている「1日に食べるリンゴの数」×4日分の合計が8個になるということになります。つまり、
$\text{?} \times 4 = 8$
という等式の「?」が答えの数ということになります。
これは9×9までの掛け算を覚えていればわかりますね。$2 \times 4 = 8$だったわけですから、「?」に入るのは2です。
よって、答えは2個ということになります。
このような「数を等しく分ける」という操作は掛け算に戻って考えればわかりますが、直接計算する方法もあります。それが割り算と呼ばれるものです(除法とも言います)。割り算を表す記号÷を使うと、今回の状況は次のような等式として表現できます。
$8 \div 4 = 2$
÷は「左の数を右の数で割る」という意味です。「左の数を右の数の分だけ等しく分ける」と言いかえてもよいでしょう。また、割り算の答えを商と呼びます。
等しく分けた結果を直接表せるのが割り算の良いところですね。
ここまでの説明で気づいたかと思いますが、割り算は掛け算と真逆の関係にあります。つまり、割り算の答えを求めたい時は掛け算に戻って考えればよいわけです。これは足し算と引き算が真逆の関係であることに似ていますね。
なので、改めて掛け算には(9×9まででよいので)しっかり慣れておきましょう!
割り切れる時と割り切れない時
実は、割り算は計算によって結果が2パターンに分かれます。
パターン1:割り切れる時
次の割り算を計算してみてください。
$15 \div 3$
割り算は掛け算の反対ですから、次のように考えられます。
$15 \div 3 = \text{?}$ ⇔ $\text{?} \div 3 = 15$
$5 \div 3 = 15$なので、答えは5ですね。
$15 \div 3 = 5$
パターン2:割り切れない時
次の割り算はどうでしょうか?
$17 \div 3$
先ほどと同じように掛け算に戻って考えてみましょう。
$17 \div 3 = \text{?}$ ⇔ $\text{?} \div 3=17$
「3を掛けて17になる数なんかあったっけ?」と思った方、その通りです。
このように割り算によっては掛け算に戻ってもうまくいかないことがあります(ゴリ押しする方法もありますが)。そんな時は、正直にそう書いてしまって大丈夫です。どういうことかというと、「割れる分だけ割ったけど、あとは余っちゃった」と書けばよいです。
わかりやすく一旦話をリンゴに置き換えて考えてみましょう。今回の計算は「リンゴが17個あり、それを同じ数ずつ3日に分けて食べたい」という話になります。
掛け算に戻って考えると$5 \times 3 = 15$なので、1日5個までなら分けることができますが、2個は余ってしまいます。
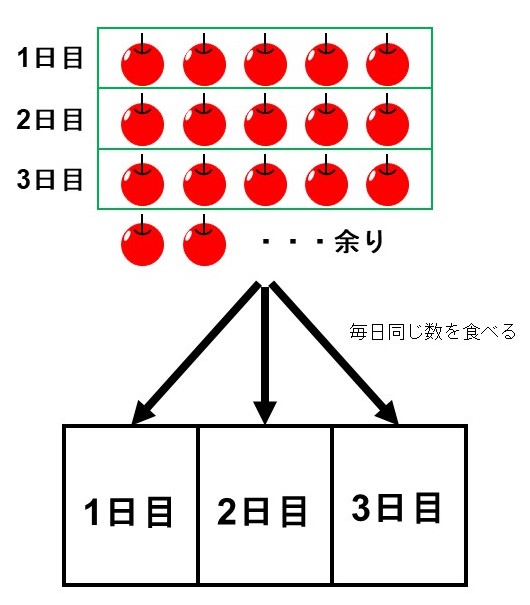
なので、割り切れなかった分(余り)も含めて次のように書いてください。
$17 \div 3 = 5 \hspace{2pt} \text{…} \hspace{2pt} 2$
これでOKです。ちなみに、割り算の余りは剰余(じょうよ)と呼ばれることもあります。
念のため、割り切れない時の計算をもう一度確認しておきましょう。
- いつも通り掛け算に立ち戻って考える
- 割り切れる分だけ求めたら、残りは余りとして書いておく
0の入った割り算は?
割り算で0が出てきた時にどうなるかも確認しておきます。最初のリンゴの例を連想しながら考えてみましょう。
(1) 0を数で割る場合
これはリンゴが全くないことになるので、
$0 \div 4=0$
となります。
(2) 数を0で割る場合
0日に分けて食べたいとはどういうことでしょうか。「今すぐ8個全部食べる」ということなのでしょうか。でもそれでは1日で食べたことになってしまうような気もします。「0日とは一体…」という感じで悩んでしまいますね。(もはや哲学?)
実は数を0で割ることは認められていません。正確には定義されていません。よって、8÷0という式は書けません。
嘘だと思うのであれば電卓を使って計算してみてください。恐らくエラーになりますよ(もしかしたら知らない人多いかも?)。
なぜそんなことになっているのかについては、ここまでの内容だけでは少し説明しにくいので、また別の機会でお話しします。
他の計算方法と一緒に出てきたときの計算順
割り算が他の計算方法(足し算・引き算・掛け算)と混ざって出てきた時の扱い方も見ておきましょう。結論を言うと、優先順位はカッコの中 → 掛け算・割り算 → 足し算・引き算となっています。
(例1)
$5 \times 4 + 6 \div 2-19$
まず、掛け算と割り算から計算します。$5 \times 4 = 20$、$6 \div 2 = 3$なので、
$\begin{align}
& \hspace{13pt} 5 \times 4 + 6 \div 2-19 \\[1.5ex]
& = 20 + 3-19
\end{align}$
後は足し算と引き算だけになったので前から計算していってください。
$\begin{align}
& \hspace{13pt} 5 \times 4 + 6 \div 2-19 \\[1.5ex]
& = 20 + 3-19 \\[1.5ex]
& = 23-19 \\[1.5ex]
& = 4
\end{align}$
(例2)
$7 \times (9-7)-9 \div (4-1) + 2 \times 2$
カッコがある場合はカッコの中の計算を優先します。$9-7 = 2$、$4-1 = 3$なので、
$\begin{align}
& \hspace{13pt} 7 \times (9-7)-9 \div (4-1) + 2 \times 2 \\[1.5ex]
& = 7 \times 2-9 \div 3 + 2 \times 2 \\[1.5ex]
\end{align}$
続いて、掛け算と割り算を計算します。$7 \times 2 = 14$、$9 \div3 = 3$、$2 \times 2 = 4$なので、
$\begin{align}
& \hspace{13pt} 7 \times (9-7)-9 \div (4-1) + 2 \times 2 \\[1.5ex]
& = 7 \times 2-9 \div 3 + 2 \times 2 \\[1.5ex]
& = 14 – 3 + 4
\end{align}$
最後に、足し算と引き算を計算します。
$\begin{align}
& \hspace{13pt} 7 \times (9-7)-9 \div (4-1) + 2 \times 2 \\[1.5ex]
& = 14-3 + 4 \\[1.5ex]
& = 11 + 4 \\[1.5ex]
& = 15
\end{align}$
まとめ
今回は割り算(除法)について学びました。まとめると次のようになりますね。
- 割り算は掛け算と真逆の関係 → 掛け算に戻って考えればよい
- 割り切れない時は割り切れた分(商)と余り(剰余)を両方書く
- 計算の順番はカッコの中 → 掛け算・割り算 → 足し算・引き算
今回で四則演算(加減乗除)が全て出そろいました。特に計算の順番は記憶があいまいになりやすいので、例を参考にしつつ、計算しながら覚えていきましょう。
今回はここまでです。お疲れさまでした!