T4　「プレゼント交換会を成功させるには？」 ― 完全順列と漸化式

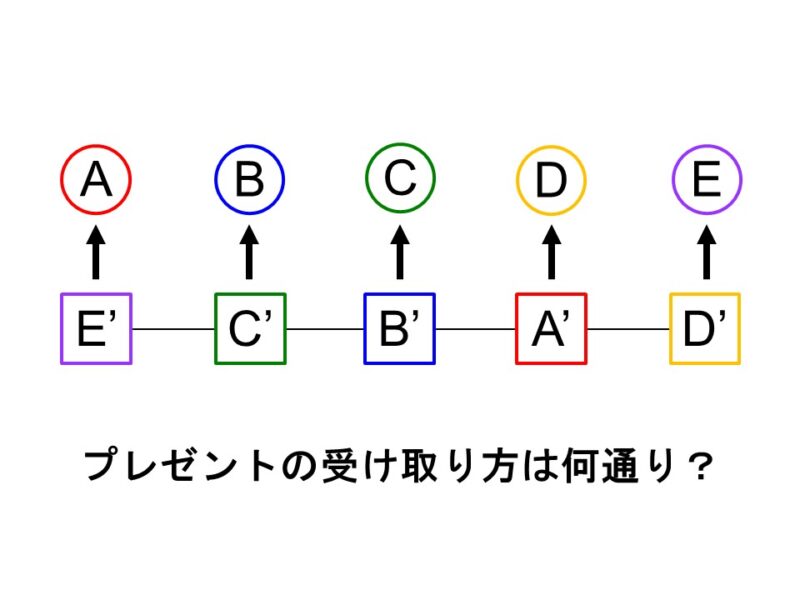
今回の問題はこちらです。（※22Fまでの内容を理解していることが前提です！）

これまで学んだこと（樹形図・順列・組合せ）を使って数えてみましょう。

(1) 3人の場合

3人であれば場合の数も少ないので、いろいろ考えるよりも全てのパターンを書き出した方が早いですね。樹形図を使いましょう。

A, B, Cの持ち寄ったプレゼントをそれぞれA’, B’, C’（‘はプライムと呼びます）と表すことにします。自分のプレゼントを受け取ってしまう組み合わせにならないように樹形図を描いてみると、考えられるのは次の2通りしかありません。

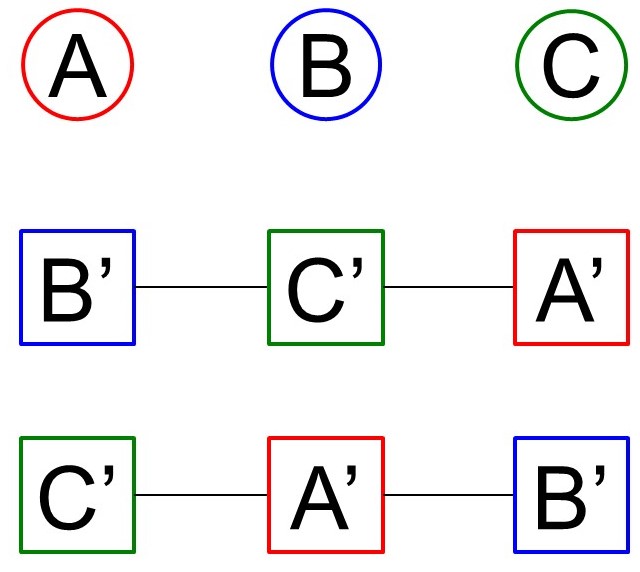
(2) 4人の場合

(1)と同じく、樹形図で数えてみましょう。場合の数も増えますから、描く時は受け取る人とプレゼントの対応に気をつけてください。

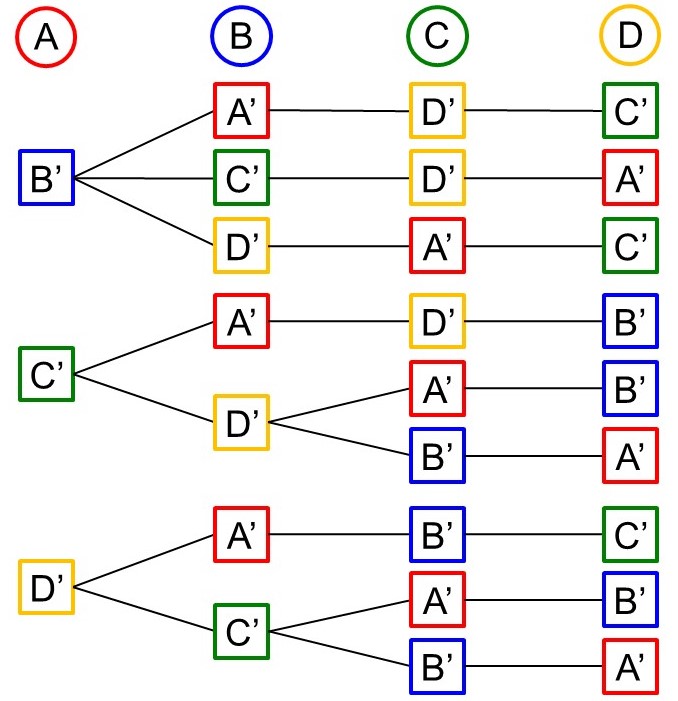
答えは9通りですね。

こうして樹形図を描いてみるとわかりますが、今回考えている場合の数というのは、掛け算で直接計算できるほど単純ではありません。4人の場合はひとまず樹形図で数えることができましたが、もっと人数が増えた場合はちょっと大変そうです…

では、樹形図の他にうまく数える方法はないのでしょうか？少し考えてみましょう。

「全員が自分以外のプレゼントを受け取る」場合の数が数えにくい一番の理由は、受け取る人とプレゼントの対応関係にかなりの注意をはらう必要があるからです。では、逆の状況である「自分のプレゼントを受け取る人がいる」場合の数も数えにくいのでしょうか？

[1] 4人全員が自分のプレゼントを受け取る場合

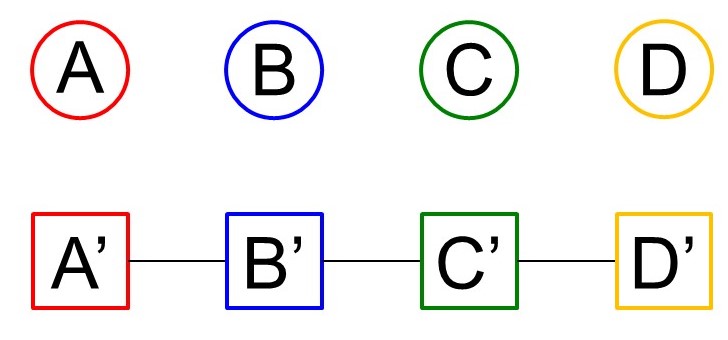
もちろん1通りしかありません。

[2] 3人が自分のプレゼントを受け取る場合

この場合、結局残りの1個のプレゼントについても、持ってきた人が自分で受け取ることになるので、状況が[1]と同じになってしまいます。なので、これは0通りです。

[3] 2人が自分のプレゼントを受け取る場合

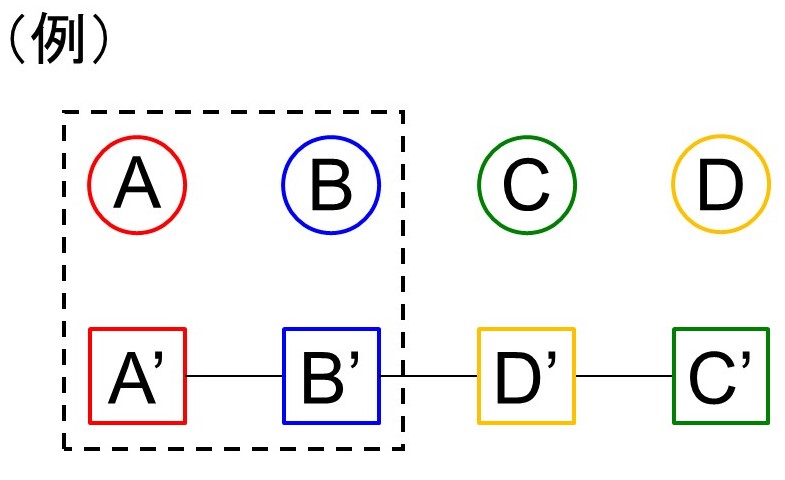
樹形図を使ってもよいですが、これは計算で求めることができます。すなわち、自分のプレゼントを受け取る人の選び方は、4人から2人を選ぶ場合の数なので₄C₂=6通り、これに対して残り2人が自分以外のプレゼントを受け取る場合の数は、1通り（お互いがプレゼントを交換した場合）しかないので、

$6 \times 1 = 6$

よって、6通りです。

[4] 1人だけが自分のプレゼントを受け取る場合

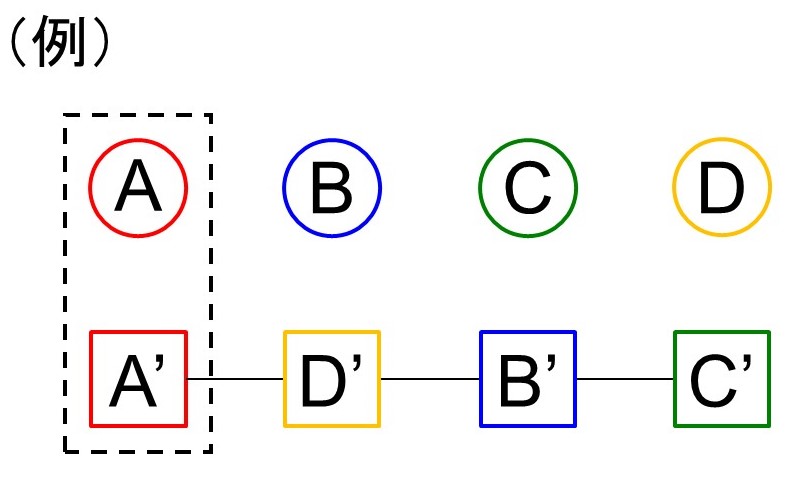
これも計算で求めることができます。すなわち、自分のプレゼントを受け取る人の選び方は、4人から1人を選ぶ場合の数なので₄C₁=4通り、これに対して残り3人が自分以外のプレゼントを受け取る場合の数は、(1)で求めたように2通りしかないので、

$4 \times 2 = 8$

よって、8通りです。

以上から、自分のプレゼントを受け取る人がいる場合の数は

$1+0+6+8 = 15$

となり、15通りであることがわかります。

確かに場合分けはありますが、それぞれの場合の数が計算で簡単に求まるので、全員が自分以外のプレゼントを受け取る場合よりも数えやすいですね。

ところでこれを使うと、元々求めたかった場合の数も計算することができます。22Fでも同じような話をしましたが、今回考えられる状況は「全員が自分以外のプレゼントを受け取る」または「自分のプレゼントを受け取る人がいる」の2通りに必ず分かれます。

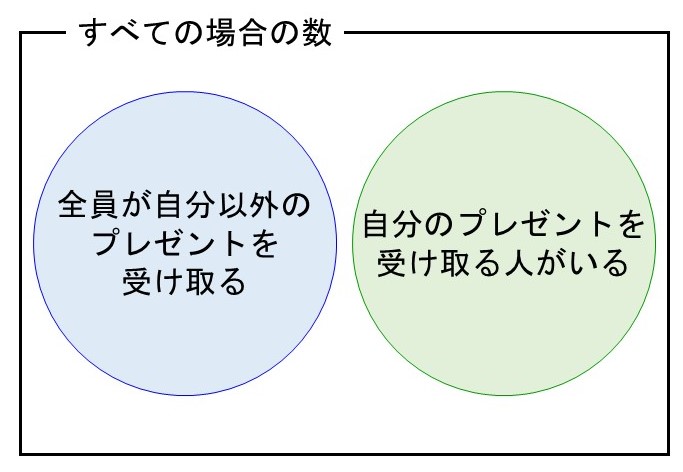
ということは、「すべての場合の数」から先ほど計算した「自分のプレゼントを受け取る人が出てくる場合の数」を差し引くことで、「全員が自分以外のプレゼントを受け取る場合の数」もわかると言えます。

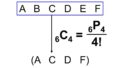
すべての場合の数については簡単に計算できます。これは、「Aが受け取るプレゼントはA’～D’の4通り、Bが受け取るプレゼントはAが受け取ったプレゼント以外の3通り、…」と考えていけば、次のような計算でよいはずです。

$4 \times 3 \times 2 \times 1 = 24$

つまり、24通りです。人もプレゼントも区別ができるので、4個のプレゼントの順列として場合の数が計算できている（=4!）のがわかりますね。

よって、求める場合の数は

$24-15 = 9$

となり、樹形図で求めた答えと同じになりました。

(3) 5人の場合

(2)と同じように、（すべての場合の数）－（自分のプレゼントを受け取る人がいる場合の数）という方法で場合の数を求めてみましょう。

[0] 起こりうるすべての場合

これは「5個のプレゼントの順列」として場合の数を考えればよいので、

$5! = 5 \times 4 \times 3 \times 2 \times 1 = 120$

つまり、120通りです。

[1] 5人全員が自分のプレゼントを受け取る場合

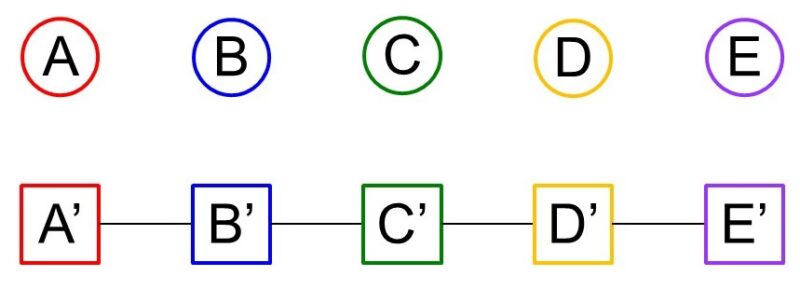
図に示すように、1通りしかありません。

[2] 4人が自分のプレゼントを受け取る場合

この場合、残りの1個のプレゼントについても持ってきた人が自分で受け取ることになるので、状況が[1]と同じになります。なので、0通りです。

[3] 3人が自分のプレゼントを受け取る場合

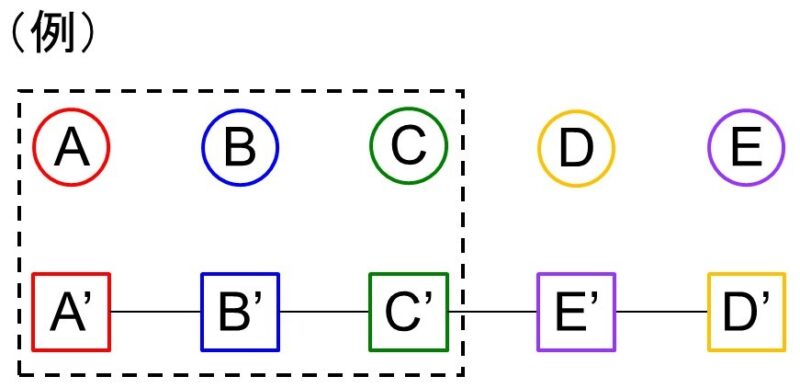
自分のプレゼントを受け取る人の選び方は、5人から3人を選ぶ場合の数なので₅C₃=10通り、これに対して残り2人が自分以外のプレゼントを受け取る場合の数は1通り（お互いがプレゼントを交換した場合）しかないので、

$10 \times 1 = 10$

よって、10通りです。

[4] 2人が自分のプレゼントを受け取る場合

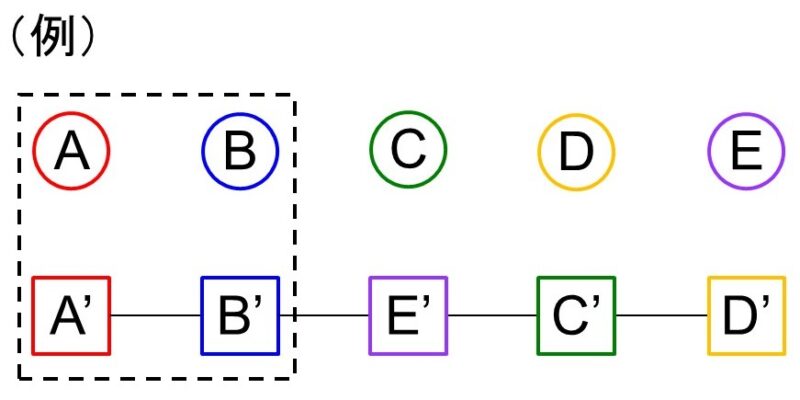
自分のプレゼントを受け取る人の選び方は「5人から2人を選ぶ場合の数」なので₅C₂=10通り、これに対して残り3人が自分以外のプレゼントを受け取る場合の数は(1)から2通りなので、

$10 \times 2 = 20$

よって、20通りです。

[5] 1人が自分のプレゼントを受け取る場合

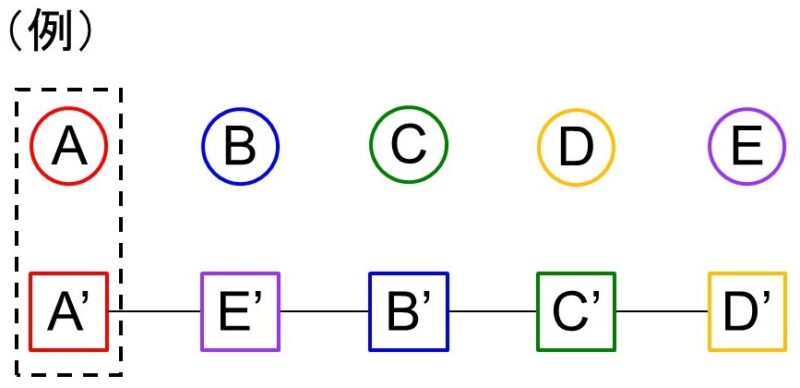
自分のプレゼントを受け取る人の選び方は「5人から1人を選ぶ場合の数」なので₅C₁=5通り、これに対して残り4人が自分以外のプレゼントを受け取る場合の数は(2)から9通りなので、

$5 \times 9 = 45$

よって、45通りです。

以上から、求める場合の数は

$120-(1+0+10+20+45) = 44$

すなわち、44通りとなります（樹形図だと大変ですね…）。

完全順列と漸化式

今回のように、「すべての要素について、対応関係が異なるように並べる順列」は完全順列（かんぜんじゅんれつ）と呼ばれており、その場合の数については次の一般式が成り立つことも知られています。すなわち、n人でプレゼントを交換する時、全員が自分以外のプレゼントを受け取る場合の数をa_nとすると、

$a_n = (n-1)(a_{n-1}+a_{n-2})$

が成り立ちます（掛け算の記号×は省略）。ただし、nは3以上の数であり、a₁=0, a₂=1です。

この等式が言っているのは、「参加者がn人の時の場合の数は、参加者がn－1人の時とn－2人の時の場合の数から求めることができる」ということです。実際、参加者が4人や5人の時には、場合の数を求めるのに、その前で求めた答えを使っていることに気づいたかと思います。

この等式が本当に成り立つか、試しにn=5の場合（5人の場合）で確かめてみましょう。

$\begin{align}
a_5 & = (5-1) \times (a_4+a_3) \\[1.5ex]
& = 4 \times (9+2) \\[1.5ex]
& = 44
\end{align}$

確かに(3)で求めた答えと同じになりましたね。このように、前の結果を使って次の結果を求めるような式を漸化式（ぜんかしき）と呼びます。また、漸化式をうまく変形すれば、a_nが実際にはどんな式で表されるのか（一般項といいます）も求めることができます。

漸化式については、また別の機会に詳しくお話しします。