こんにちは、まてがめです。
前回は「順列」について学びました。「物を順番に並べる」というシンプルなものですが、物が一列に並ばない状況でも場合の数を考えるのに応用できるという話をしました。
前回に続き今回も、いろんな場面で場合の数を調べるのに応用できる考え方を学びます。それが組合せです。
「起こりうる組合せについて考える」というのは、もはや順番を気にしなくてもよいわけですから、もしかすると前回とは全く別の話に聞こえるかもしれません。ですが、むしろその逆です。実は、順列の考え方の延長上に組合せの考え方があります。
組合せ
組合せでは「何の要素からできているのか」のみを考えて場合の数を数えます。そのため順列とは異なり、要素の並び順は関係ありません。例を見ながら理解していきましょう。
例1 グループを作る
Aさん、Bさん、Cさん、Dさん、Eさん、Fさんの6人がいる。この6人から次の方法でグループを作ることにした。
(1) 4人のグループを1つ作る
(2) 2人のグループを3つ作る
この時、グループの作り方はそれぞれ何通りあるか?
(1) 4人のグループを1つ作る
まずはイメージをつかむために、どんな組み合わせが考えられるのか試してみましょう。例えば、次のようなグループが考えられますね。
(A B C D)
並び順は考えないので、次のグループも上と同じものとしてカウントします。
(C A D B)
ここで、あえて思い出してほしいのが順列です。実は順列においても、並び順を区別しない場面があったことを覚えているでしょうか?それは、並べる物が区別できない時です。
その時はどうしたかというと、「一旦区別できるとみなしてから場合の数を計算し、最後に重複している分で割って、その区別をなくす」という方法を使いました。この方法を今回の問題にも活かせないでしょうか?
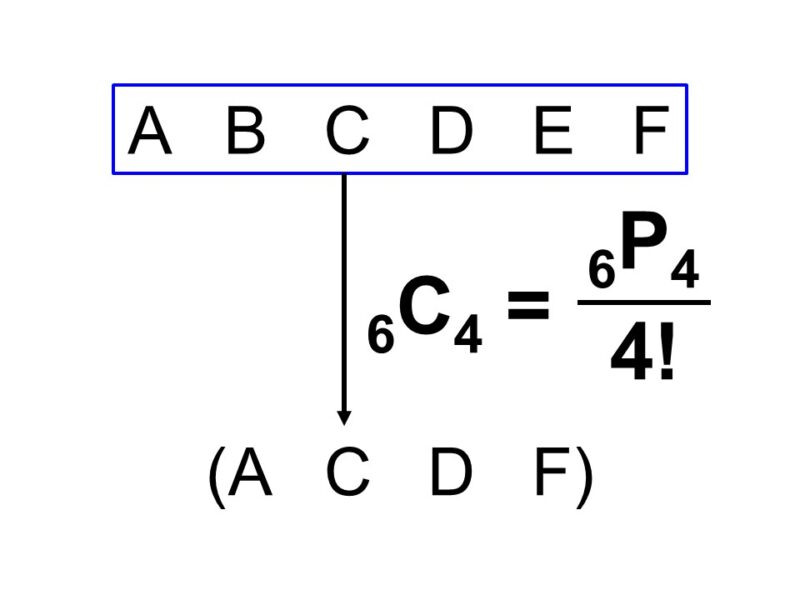
まず、一旦並び順が区別できるとみなして場合の数を計算してみます。その場合、「6人から4人を選んで一列に並べる順列」について考えることになるので、場合の数は
${}_6 \mathrm{P}_4 = 6 \times 5 \times 4 \times 3$
と表せます(約分が控えているので、ここでは計算しません)。
次に、重複分で割って、並び順の区別をなくします。例えば、A, B, C, Dの4人がこの順列に参加したとすると、この4人がどのように並んだとしても、組合せにおいては区別がつかないわけです。そしてこの4人の並べ方は
$4! = 4 \times 3 \times 2 \times 1$
と表せるので、順列で考えてしまうとこれだけ重複があることになります。よって、求める場合の数は
$\dfrac{{}_6 \mathrm{P}_4}{4!} = \dfrac{6 \times 5 \times 4 \times 3}{4 \times 3 \times 2 \times 1}=15$
すなわち、15通りとなります。
このように、組合せは順列の考え方をベースにすることで場合の数を数えることができます。
ところで、今回の問題は「組合せ」だからこそできる別の考え方があります。それは、「逆の組合せについて考える」ということです。
すなわち、「6人からグループを作るための4人を選ぶ」ことと「6人からグループに入らない2人を選ぶ」ことが1対1に対応しているので、こちらの場合の数を計算してもよいということです。
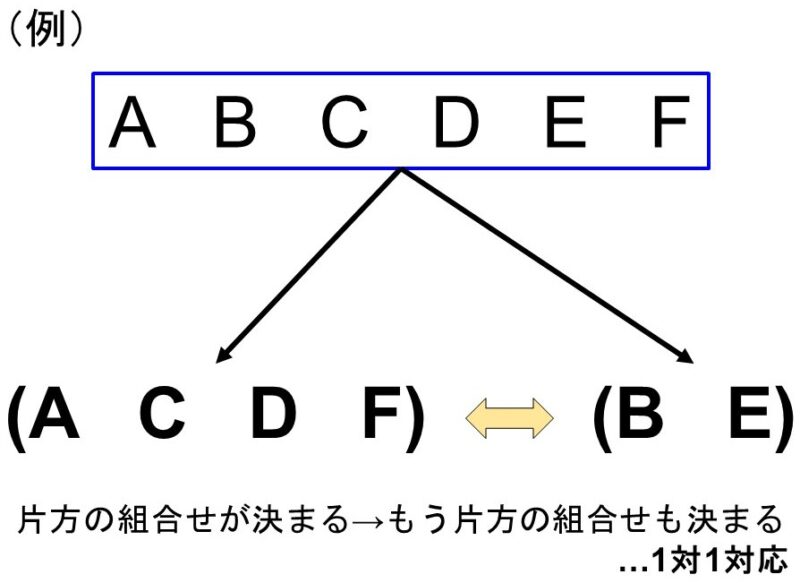
この場合、「6人から2人を選んで作る組合せ」を考えればよいので、求める場合の数は
${}_6 \mathrm{C}_2 = \dfrac{6 \times 5}{2 \times 1} = 15$
となります。組合せにおける要素の数が少ない分、こちらの方が計算は簡単です。
(2) 2人のグループを3つ作る
これは「6人から2人を選んでグループを作り、残り4人から2人選んでグループを作り、最後に残った2人でグループを作る」と考えてみましょう。
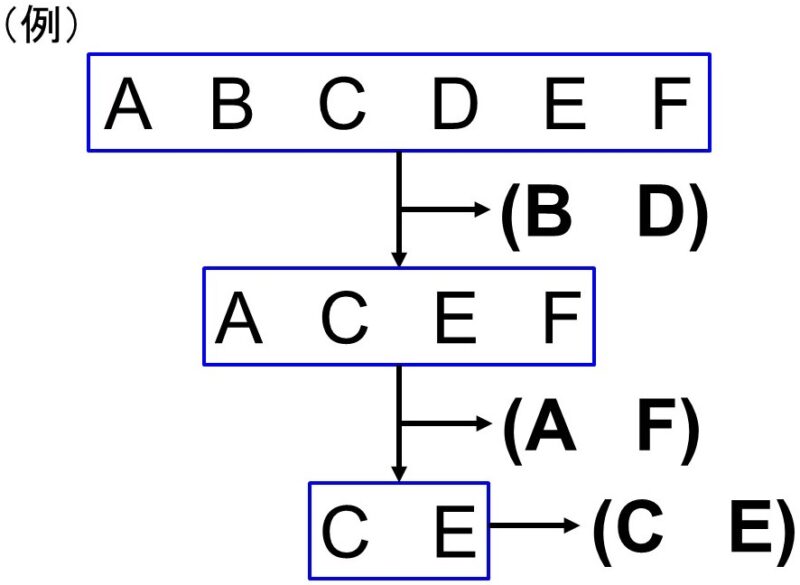
つまり、6人から2人1組の組合せを順番に作っていくことになるので、求める場合の数は
$\begin{align}
& \hspace{13pt} {}_6 \mathrm{C}_2 \times {}_4 \mathrm{C}_2 \times {}_2 \mathrm{C}_2 \\[1.5ex]
& = \dfrac{6 \times 5}{2 \times 1} \times \dfrac{4 \times 3}{2 \times 1} \times \dfrac{2 \times 1}{2 \times 1} \\[1.5ex]
& = 15 \times 6 \times 1 \\[1.5ex]
& = 90
\end{align}$
つまり、90通りとなります。
例2 玉の取り出し
組合せの考え方に慣れるために、もう一つ例を考えてみましょう。
袋の中に赤玉が2個、青玉が3個、緑玉が4個入っており、玉には色ごとに1, 2, …と番号が書かれている。ここから中身を見ずに3個の玉を同時に取り出す。
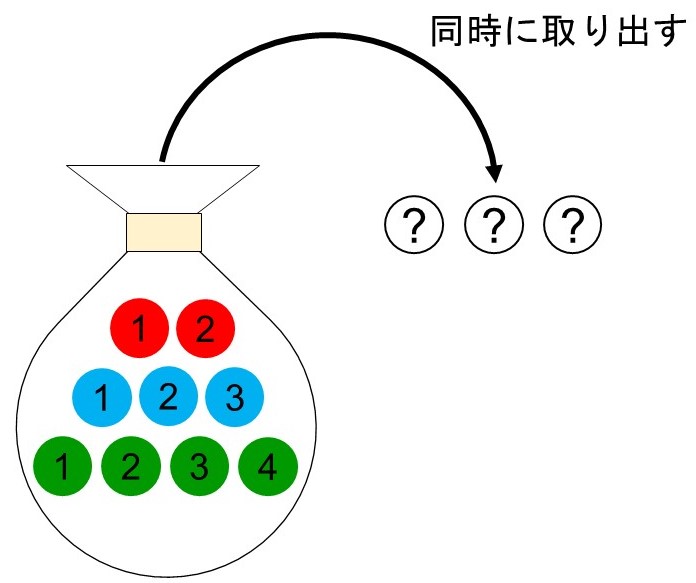
この時、次の場合の数はそれぞれ何通りか?
(1) 起こりうるすべての取り出し方
(2) 緑玉以外を取り出す
(3) 取り出した玉の中に1個だけ青玉が含まれている
(4) 取り出した玉の中に少なくとも1個は1と書かれた玉が含まれている
(1) 起こりうるすべての取り出し方
玉を「同時に取り出す」ので、取り出した順番などは気にする必要がなく、組合せのみを考えることになります。玉はそれぞれ色と数字で区別できますから、9個の玉から3個選ぶ場合の数を計算すればよいですね。
${}_9 \mathrm{C}_3 = \dfrac{9 \times 8 \times 7}{3 \times 2 \times 1}=84$
よって、答えは84通りとなります。
(2) 緑玉以外を取り出す
「緑玉以外を取り出す」ということは、「赤玉か青玉の中から3個取り出す」ということになります。
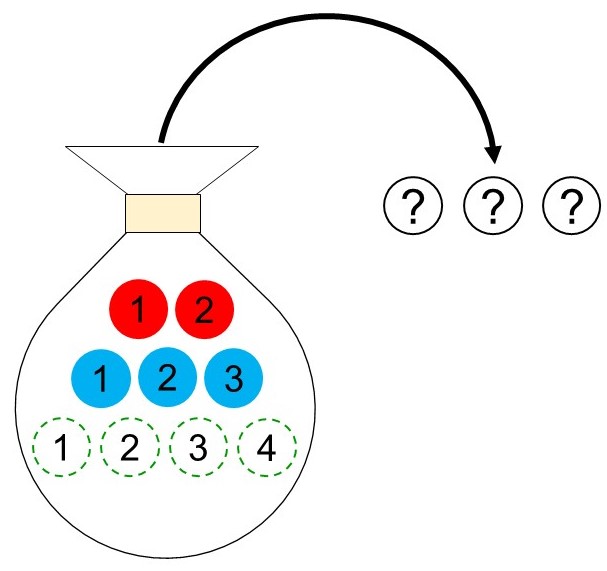
したがって、5個の玉から3個選ぶ場合の数を計算すればよいので、
${}_5 \mathrm{C}_3 = \dfrac{5 \times 4 \times 3}{3 \times 2 \times 1} = 10$
よって、答えは10通りとなります。
(3) 取り出した玉の中に1個だけ青玉が含まれている
「青玉が1個だけ含まれる」ので、青玉とそれ以外の玉で状況を分けて考えてみましょう。
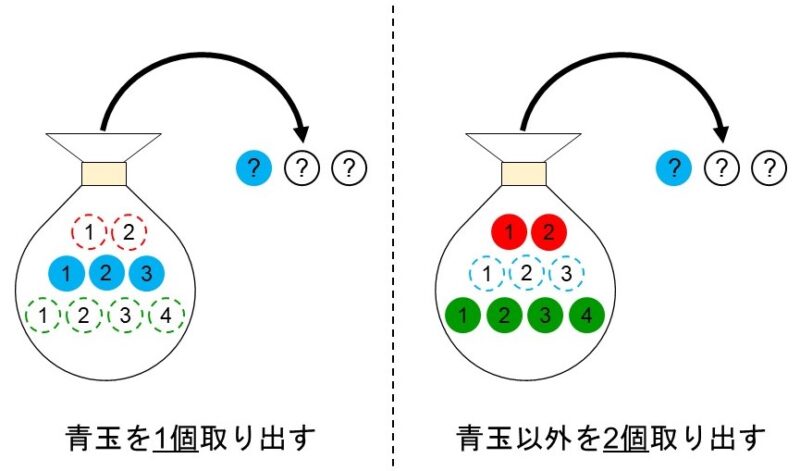
まず青玉の取り出し方ですが、青玉は3個あるので、3個の玉から1個選ぶ場合の数として計算できます(要素が1個でも組合せとみなすことはできます)。
${}_3 \mathrm{C}_1 = \dfrac{3}{1}=3$
この3通りに対して、残りの玉の取り出し方を考えます。残り2個は赤玉か緑玉から選ばれることになるので、6個の玉から2個を選ぶ場合の数を計算すればよいことになります。
${}_6 \mathrm{C}_2 = \dfrac{6 \times 5}{2 \times 1} = 15$
したがって求める場合の数は、これらの積になるので、
$3 \times 15 = 45$
答えは45通りとなります。
(4) 取り出した玉の中に少なくとも1個は1と書かれた玉が含まれている
1の玉は各色で1個ずつ計3個あります。「少なくとも1個は」ということは、1の玉が[1] 1個含まれている時、[2] 2個含まれている時、[3] 3個含まれている時の3通りが考えられるので、それぞれについて場合の数を計算する必要があります。
[1] 1個含まれている時
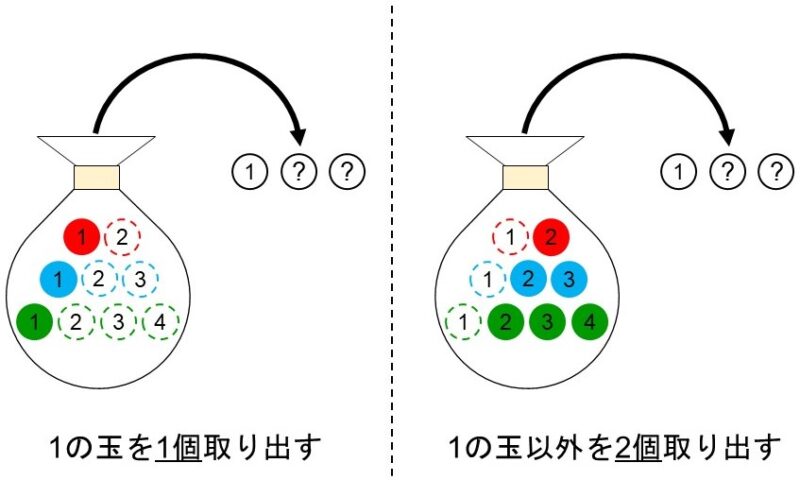
(3)での考え方を踏まえて計算してみましょう。1の玉については3個の玉から1個選ぶ場合の数、残り2個の玉については6個の玉から2個選ぶ場合の数を計算すればよいので、求める場合の数は
$\begin{align}
& \hspace{13pt} {}_3 \mathrm{C}_1 \times {}_6 \mathrm{C}_2 \\[1.5ex]
& = \dfrac{3}{1} \times \dfrac{6 \times 5}{2 \times 1} \\[1.5ex]
& = 3 \times 15 \\[1.5ex]
& = 45
\end{align}$
すなわち、45通りです。
[2] 2個含まれている時
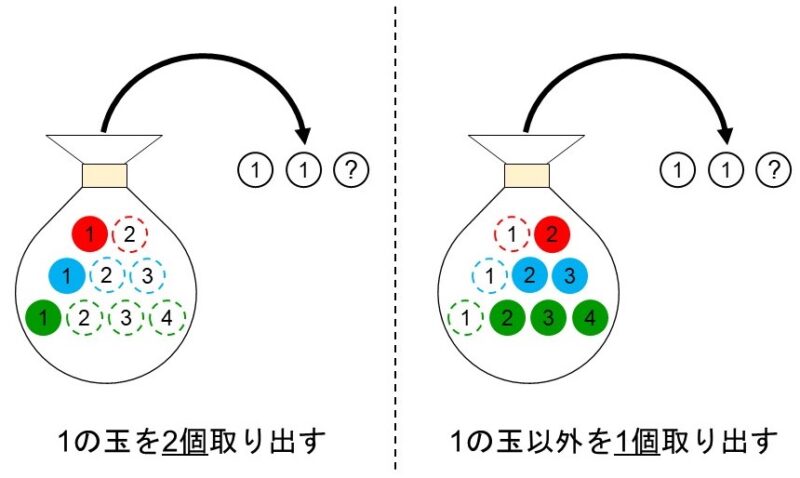
1の玉については3個の玉から2個選ぶ場合の数、残り1個の玉については6個の玉から1個選ぶ場合の数を計算すればよいので、求める場合の数は
$\begin{align}
& \hspace{13pt} {}_3 \mathrm{C}_2 \times {}_6 \mathrm{C}_1 \\[1.5ex]
& = \dfrac{3 \times 2}{2 \times 1} \times \dfrac{6}{1} \\[1.5ex]
& = 3 \times 6 \\[1.5ex]
&=18
\end{align}$
すなわち、18通りです。
[3] 3個含まれている時
1の玉は3個しかないので、3個の玉から3個選ぶ場合の数として計算できます。一応次のように計算できますが、もちろん1通りです。
${}_3 \mathrm{C}_3 = \dfrac{3 \times 2 \times 1}{3 \times 2 \times 1} = 1$
[1]~[3]で求めた場合の数を足し合わせれば、元々求めたかった場合の数になるので、
$45+18+1 = 64$
つまり、64通りが答えとなります。
例3 2チームの試合
一見すると組合せが関係ないように見える状況でも、工夫すると組合せの考え方を使うことができます。次の例を見てください。
ある競技において、AさんとBさんは実力がほぼ互角である。そこで、より公平に勝者を決めるために「先に4勝した方を勝者とする」というルールで2人に試合を行ってもらうことにした。
この時、勝者が決まる時の試合結果は何通りあるでしょうか?
手当たり次第に数えようとするとさすがにキリがないので、順を追って考えてみましょう。
まず「勝者が決まる」ということは「AもしくはBが勝者になる」ということですが、勝者の決め方に優劣はない(どちらかが有利あるいは不利ということはない)ので、どちらかが勝者となる場合の数を数え、それを2倍すれば答えが求まります。なので、ここでは「Aが勝者となる場合」について考えることにしましょう。
また、「先に4勝した方を勝者とする」ということは「3回までなら負けてもよい」ということになります。したがって、試合数は4(負けなし)、5(負けが1回)、6(負けが2回)、7(負けが3回)の4通りであることがわかります。
ここで「勝ち=○、負け=×」とした表を使うと、組合せの問題として場合の数を調べることができます。
(1) 試合数:4
これはAが負けることなく4勝する場合です。
| 1 | 2 | 3 | 4 | |
| A | ○ | ○ | ○ | ○ |
| B | × | × | × | × |
表に示す通り、1通りしかありません。
(2) 試合数:5
これはAが4勝するまでに1敗する場合ですから、例えば次のような状況が考えられます。
| 1 | 2 | 3 | 4 | 5 | |
| A | ○ | × | ○ | ○ | ○ |
| B | × | ○ | × | × | × |
5試合目に勝って勝者になるので、1~4試合目のどこかで必ず1回負けることになります。これを表で考えると「1~4までの4つの枠のうち1つに×がつく」ということになります。
これは4個のものから1個選ぶ場合の数として考えることができるので、
${}_4 \mathrm{C}_1 = \dfrac{4}{1} = 4$
よって、4通りです。
(3) 試合数:6
これはAが4勝するまでに2敗する場合ですから、例えば次のような状況が考えられます。
| 1 | 2 | 3 | 4 | 5 | 6 | |
| A | × | ○ | ○ | × | ○ | ○ |
| B | ○ | × | × | ○ | × | × |
6試合目に勝って勝者になるので、1~5試合目のどこかで必ず2回負けることになります。これを表で考えると「1~5までの5つの枠のうち2つに×がつく」ということになります。
これは5個のものから2個選ぶ場合の数として考えることができるので、
${}_5 \mathrm{C}_2 = \dfrac{5 \times 4}{2 \times 1} = 10$
よって、10通りです。
(4) 試合数:7
これはAが4勝するまでに3敗する場合ですから、例えば次のような状況が考えられます。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| A | ○ | × | ○ | ○ | × | × | ○ |
| B | × | ○ | × | × | ○ | ○ | × |
7試合目に勝って勝者になるので、1~6試合目のどこかで必ず3回負けることになります。これを表で考えると「1~6までの6つの枠のうち3つに×がつく」ということになります。
これは6個のものから3個選ぶ場合の数として考えることができるので、
${}_6 \mathrm{C}_3 = \dfrac{6 \times 5 \times 4}{3 \times 2 \times 1} = 20$
よって、20通りです。
したがって(1)~(4)で求めた場合の数を足し合わせると「Aが勝者となる場合の数」となり、さらにこれを2倍すると「勝者が決まる時の場合の数」が求まります。
$2 \times (1+4+10+20) = 70$
よって、70通りが答えとなります。
まとめ
今回は組合せについて学びました。大切な部分をまとめます。
- n個のものからk個選んで組合せを作る場合の数は
$\begin{align}
{}_n \mathrm{C}_k & = \dfrac{{}_n \mathrm{P}_k}{k!} \\[1.5ex]
& = \dfrac{n(n-1) \text{…} (n-(k-1))}{k(k-1) \text{…} \times 2 \times 1} \\[1.5ex]
& = \dfrac{n!}{(n-k)!k!}
\end{align}$
- 「n個のものからk個を選ぶ」ことと「n個のものから目的の組合せに含まれないn-k個を選ぶ」ことは1対1に対応するので、
${}_n \mathrm{C}_k = {}_n \mathrm{C}_{n-k}$
組合せは順列のように並べる順番を考える必要がない分、応用の幅が広いです。実際、今回の例のように、現実の世界で組合せを考える場面が多いのはもちろんのこと、数式の計算にも組合せが使われます(また別の機会で解説します)。なので、組合せを数え上げるための方法はよく理解しておきましょう。
前回も言いましたが、公式はあくまでも結果として生まれたものであり、最初に覚えるべきは「その考え方(=順列を考えておいてから並べ方の区別をなくす)」です。考え方がマスターできれば、自然と公式も理解して扱えるようになりますよ。
今回はここまでです。お疲れさまでした!