こんにちは、まてがめです。
前回は、起こりうる場合の数を知る方法として「樹形図」を学びました。
場合の数を調べる時、樹形図はあらゆる状況に対応できるので、方針が立たない時はぜひとも試したい方法です。しかしその一方、樹形図には「場合の数が多すぎる状況では描くのに時間がかかりすぎる」というデメリットもあります。なので、物事を考えるのにいつも樹形図を描くというわけにもいきません…（できることなら楽がしたい！！）
そこでまずは、「場合の数の数え方がわかっている状況に置きかえられないか？」ということを考えていくことになります。「初めて見る状況」を「すでに知っている状況」に置きかえることができれば、簡単に場合の数を調べることができるからですね。
この「置きかえ」を行う上で覚えておきたいのが、今回学ぶ順列（じゅんれつ）と呼ばれるものです。
順列
順列（じゅんれつ）とは、人や物に順番を決めて並べた列のことを指します。それ自体は単純なものですが、順列における場合の数をどうやって数えるのかを知っておくと、いろいろな場面で応用することができます。
例1 人を並べる
まずは簡単な例から見てみましょう。
Aさん、Bさん、Cさん、Dさん、Eさん、Fさんの6人がいる。彼らに次の3つのパターンで整列してもらうことにした。
(1) 全員で1列に並んでもらう
(2) 6人の中から3人を選び、1列に並んでもらう
(3) 3人ずつ左右2列に並んでもらう
この時、それぞれの並べ方は何通りあるか？
(1) 全員で1列に並んでもらう
これについては樹形図を実際に描かなくても、樹形図をイメージしながら計算で求めることができます。すなわち、1番目にはA～Fさんの6通りがあり、その各々に対して2番目には1番目の人以外の5通りがあり、その各々に対して3番目には1番目と2番目の人以外の4通りがあり、…と考えます。そしてこれはまさに掛け算で表すことができます。
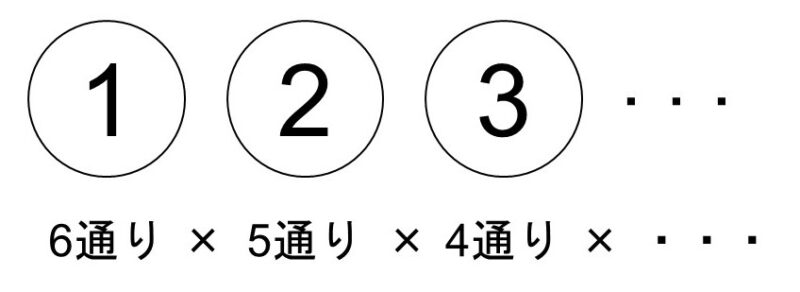
よって、求める場合の数は
$6 \times 5 \times 4 \times 3 \times 2 \times 1=720$
すなわち、720通りとなります（樹形図を描いてたら大変でした…）。
この考え方を使いまわせるように、数ではなく文字を使って考えてみましょう。これは理学においてよく用いる方法なのですが、文字を使った等式を作っておくことで、その文字に数を入れる（代入といいます）だけでどんな場合でも答えが知ることができます。
そこで、n個のものを1列に並べる場合の数を求めてみます（自然数は英語でnatural numberなので、人や物の数を表す文字にはnがよく使われます）。
1番目はn個の中から選ぶのでn通り、その各々に対して2番目は1番目以外のn－1通り、その各々に対して3番目は1番目と2番目以外のn－2通り、…と考えることができます。
よって、n個のもので順列を作る場合の数を求めるには、1番目からn番目までのそれぞれの場合の数を掛け算すればよいことがわかります。
$n \times (n-1) \times (n-2) \times \text{…} \times 2 \times 1$
ちなみに文字を使った式では、掛け算の記号×を次のように省略することが多いです。
$n(n-1)(n-2) \text{…} \times 2 \times 1$
階段のように1ずつ数を変えながら掛け算（乗法）を行うこの式は$n$の階乗（かいじょう）と呼ばれており、!の記号を使って次のように表します。
$n!=n(n-1)(n-2) \text{…} \times 2 \times 1$
文字を使った議論は、よりレベルの高い数学を学ぶのに必要なので、少しずつ慣れていきましょう。
(2) 6人の中から3人を選び、1列に並んでもらう
これは(1)と同じように考えると簡単です。すなわち、1番目としてA～Fさんの中から1人を選び（6通り）、2番目として1番目以外の中から1人を選び（5通り）、3番目として1番目と2番目以外の中から1人を選べば（4通り）、6人のうちの3人をちゃんと並べることができますね。
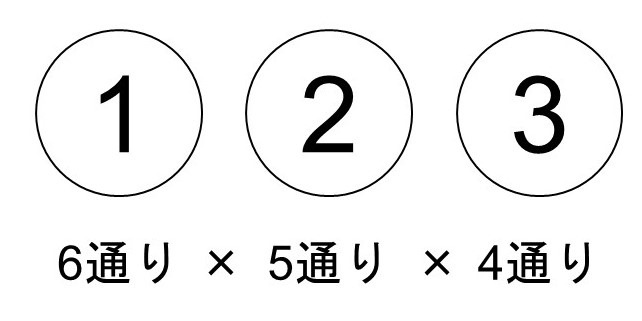
よって、求める場合の数は
$6 \times 5 \times 4=120$通り
となります。
こちらも一般的な話として、n個からk個を選んで1列に並べる場合の数を考えてみましょう。
1番目の選び方はn通り、2番目はn－1通り、…と考えられ、特に最後のk番目の選び方は、その1つ前のk－1番目までの時点ですでに選ばれているk－1個を除いたn－(k－1)通りとなります。
つまり、n個からk個を選んで順列を作る場合の数は、1番目からk番目までのそれぞれの場合の数を掛け算すればよいことがわかります（×は省略）。
$n(n-1) \text{…} (n-(k-1))$
この式は順列を意味する英語Permutationの頭文字Pを使って
${}_n \mathrm{P}_k = n(n-1) \text{…} (n-(k-1))$
と表すことがあります。
(3) 3人ずつ左右2列に並んでもらう
これはどう考えればよいでしょうか？ここで、わかりやすく考えるための工夫として、次のように「列を作るための枠を用意し、ここに左上から順番に6人を配置していく」としてみます。
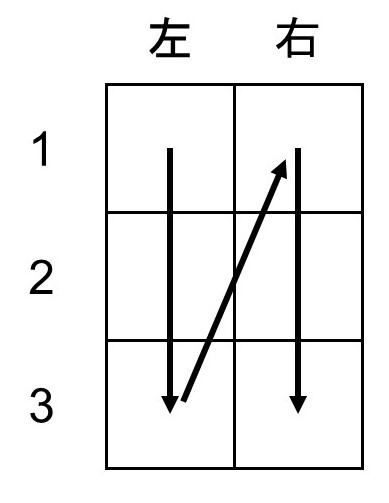
すると、左の1番目は6人から選ぶので6通り、2番目は残り5人の5通り、3番目は残り4人の4通りとなります。続いて右にいくと、右の1番目は残り3人の3通り、2番目は残り2人の2通り、3番目は残り1人の1通りとなります。よって、求める場合の数は
$6 \times 5 \times 4 \times 3 \times 2 \times 1=720$
すなわち、720通りとなります。状況は違いますが、(1)と同じ計算になっていることに気づいたでしょうか？
つまり、たとえ1列に並べるような状況でなかったとしても、「並べる人や物」と「並べる位置」がそれぞれ区別できる状況であれば、順列として場合の数を数えることができるということです。ここに順列を学ぶ意味があります。
例えば、前回の「20F 樹形図」において、袋から色のついた玉を取り出す例を紹介しました。
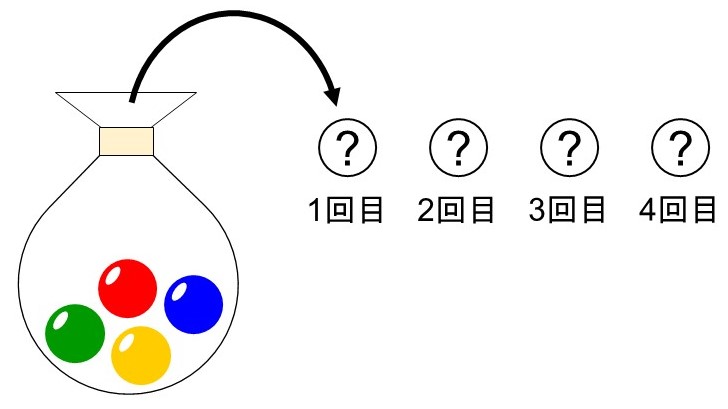
一見すると順列とは関係なさそうですが、「玉の取り出し方」と「玉の並べ方」を1対1で対応させることができる（1回目→1番目、2回目→2番目、…）ので、玉を取り出す時の場合の数は順列で考えることができます（4!=24通り）。
…では、並べる物や位置が区別できない場合はどう考えればよいでしょうか？次の例で見てみましょう。
例2 文字の並びかえ（並べる物が区別できない場合）
次の7つのアルファベット
a, a, a, b, b, c, c
を使い、次の方法で文字列を作ることにした。
(1) a, b, cの3文字のみを使って文字列を作る
(2) a, a, a, b, cの5文字のみを使って文字列を作る
(3) すべてのアルファベットを使って文字列を作る
この時、それぞれの並べ方は何通りあるか？
(1) a, b, cの3文字のみを使って文字列を作る
この場合は異なる3個のものを並べる順列なので、例1と同じように考えればよいですね。並べ方の数は
$3!=3 \times 2 \times 1=6$通り
となります。
(2) a, a, a, b, cの5文字のみを使って文字列を作る
相異なる5文字であれば(1)と同じように考えればよいですが、今回は同じaが3つあるため、このように計算すると並べ方として数えすぎていることになります。
例えば、もし3つのaがa1, a2, a3と区別できる場合、
a1-b-a2-c-a3 と a3-b-a1-c-a2
は異なる並べ方といえます。一方、今回は3つのaが区別できないため、この2つは同じ並べ方ということになります。このような状況を重複（ちょうふく）といいます。
こんな時は、あえて区別して場合の数を数えた後、その区別をなくします。どういうことか順を追って見てみましょう。
まず、3つのaがa1, a2, a3と区別できるとすると、a1, a2, a3, b, cの相異なる5文字の並べ方は
$5!=5 \times 4 \times 3 \times 2 \times 1=120$通り
となります。
次に3つのaの区別をなくすための操作を行います。そもそも3つのaを区別したことでどれだけ重複しているのかというと、それはa1, a2, a3の並べ方の分（3! = 6通り分）だけ重複しています。例えば、a-b-a-c-aという1通りの並べ方に対し、3つのaに区別をつけて数えたことで次の6通りが重複しています。
a1-b-a2-c-a3 a1-b-a3-c-a2 a2-b-a1-c-a3
a2-b-a3-c-a1 a3-b-a1-c-a2 a3-b-a2-c-a1
つまり、実際よりも6倍多く数えているということです。なので、区別をつけて考えた時の場合の数（120通り）を6で割れば、本当に知りたい場合の数が求まるといえます。よって、求める場合の数は
$\dfrac{120}{6}=20$
すなわち、20通りとなります。
このように、区別できないものを含む順列では、一度区別をつけた上で場合の数を考え、最後に区別をなくす（重複している分で割る）ことで本来の場合の数を求めます。
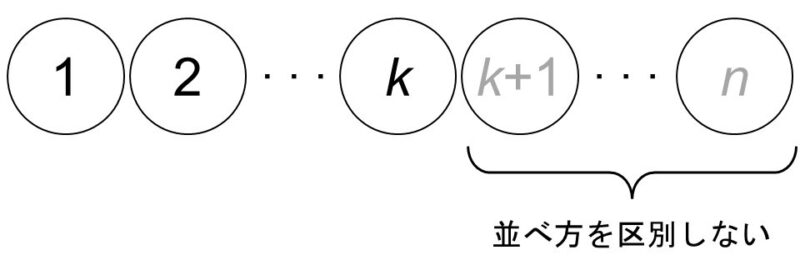
(3) すべてのアルファベットを使って文字列を作る
3つのa、2つのb、2つのcはそれぞれ区別できませんが、これは(2)を踏まえればわかりますね。まずは区別できると考えて（a1, a2, a3, b1, b2, c1, c2として）場合の数を数えると、7!通りです。
次に区別をなくします。a1, a2, a3の並べ方で3!通り分、b1, b2の並べ方で2!通り分、c1, c2の並べ方で2!通り分だけ重複して数えているので、これらで割れば求める場合の数がわかります。
$\begin{align}
&\hspace{13pt} \dfrac{7!}{3! \times 2! \times 2!} \\[1.5ex]
& = \dfrac{7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{(3 \times 2 \times 1) \times (2 \times 1) \times (2 \times 1)} \\[1.5ex]
& = 7 \times 6 \times 5 \\[1.5ex]
& = 210
\end{align}$
よって、求める場合の数は210通りとなります。
先ほど、n個のものからk個選んで並べる時の場合の数は、次のようになることを解説しました。
${}_n \mathrm{P}_k = n(n-1) \text{…} (n-(k-1))$
実はこの式、少し考え方を変えると「階乗」を使って表すこともできます。
「n個からk個を選んで順列を作る」ということは、「n個すべてを並べた後、k+1番目から後ろの順列については、どんな並べ方でも同じものとして区別しない」と考えることもできます。
その場合、まずn個の順列における場合の数はn!通りと表せます。
一方、k+1番目から後ろの順列における場合の数は、すでに選ばれているk個を除いたn–k個の順列における場合の数であり、これは(n–k)!通りとなります。
「k+1番目から後ろの順列を区別しない」ということは「場合の数をn!通りとして計算してしまうと、(n–k)!通り分だけ数えすぎている」ということなので、次のように計算すればよいことになります。
$\dfrac{n!}{(n-k)!}$
したがって、n個からk個を選んで1列に並べる場合の数は、次の3パターンで表せます。
$\begin{align}
{}_n \mathrm{P}_k & = n(n-1) \text{…} (n-(k-1))\\[1.5ex]
& = \dfrac{n!}{(n-k)!}
\end{align}$
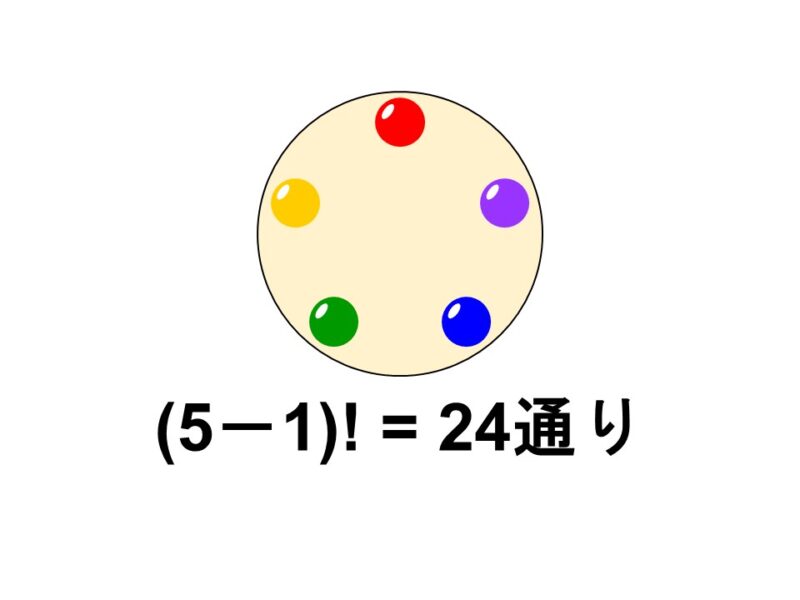
例3 円順列（並べる位置が区別できない場合）
ここに赤色、青色、黄色、緑色、紫色の5種類のビーズがある。Aさんはこれらを使って次の工作を行うことにした。
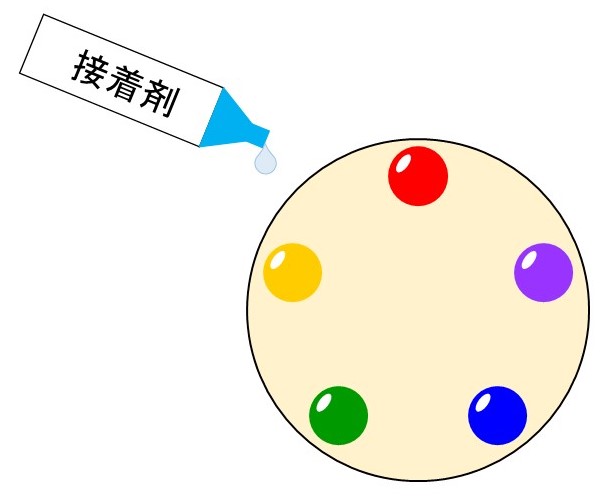
(1) 5種類のビーズすべてを1個ずつ使い、これらを丸い布に円形に接着していく
(2) 5種類のビーズすべてを1個ずつ使い、これらに糸を通して円形の飾りを作る
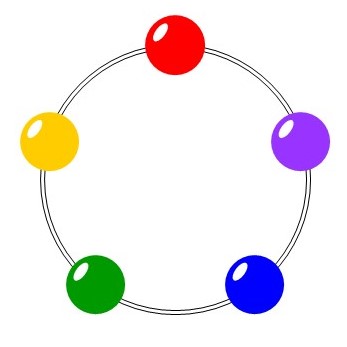
この時、ビーズの並べ方はそれぞれ何通りあるか？
(1) 5種類のビーズすべてを1個ずつ使い、これらを丸く切った布に円形に接着する
ここで注意しなくてはいけないのが「円形に」という言葉です。これが何を意味しているかというと、ビーズを置く位置に区別がないということです。
例えば、左回りに赤、黄、緑、青、紫の順番でビーズを並べるとします。しかし円形であるため、この並べ方は回転させることができます。つまり、次の5つの並べ方は区別がつきません。
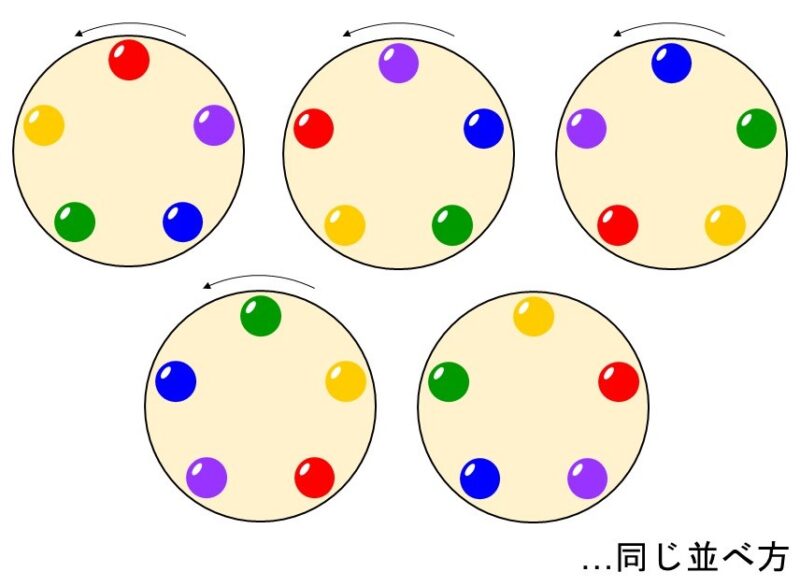
したがって、普通の順列と考えて場合の数を計算してしまうと数えすぎていることになります。ではどうするかというと、2つの方法があります。
[1] 位置に区別をつけて並べ方を数えた後、その区別をなくす
まず、回転させることができない（位置に区別がある）とすると、5個のものを並べる順列として考えることができるので、並べ方は5!通りになります。
次に区別をなくします。回転できる場合には1つの並べ方につき5通りの重複があるので、5で割れば求める場合の数となります。
$\dfrac{5!}{5}=4! = 24$
よって、並べ方は24通りとなります。
[2] 1個のビーズの位置を固定し、残りのビーズの順列として並べ方を数える
こちらは最初から重複がないようにする方法です。例えば、赤色のビーズを一か所に固定したとします。すると、このビーズから見た時の位置（相対的な位置）というものが決まります。
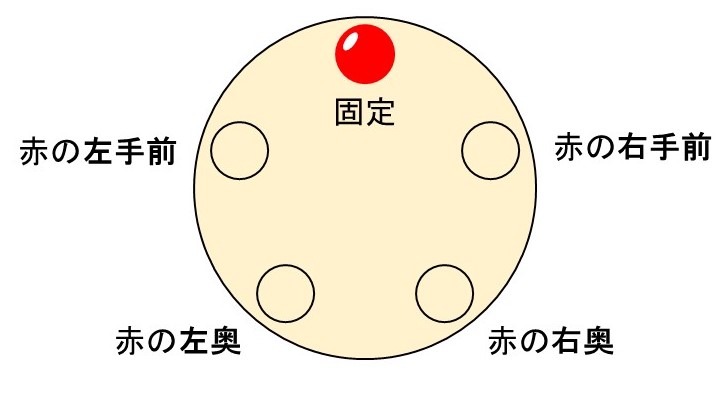
これならば位置に区別がつくので、残り4個のビーズの順列として並べ方を計算すればよいことになります。すなわち、$4! = 24$通りです。
(2) 5種類のビーズすべてを1個ずつ使い、これらに糸を通して円形の飾りを作る
円形に並べるので、(1)と同じく円順列を考えることになりますが、今回はもう一つ注意することがあります。それは「飾り」である（＝裏表がない）という点です。裏表がないということは、例えば次の２つの並べ方は区別がつきません。
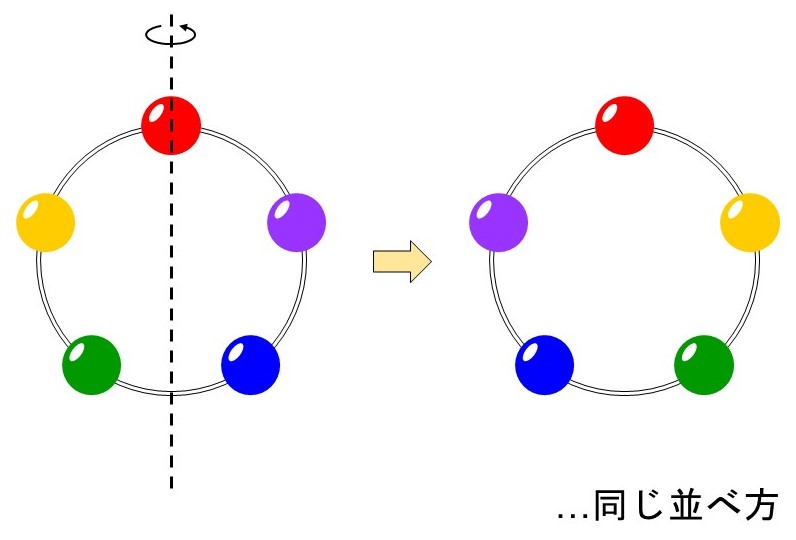
そのため、(1)のように計算してしまうと2倍多く数えていることになります。よって、(1)の答えを2で割れば本当の場合の数が求まります。
$\dfrac{24}{2} = 12$
答えは12通りですね。このように裏表がない円順列は数珠（じゅず）順列と呼ばれることがあります。
まとめ
今回は順列について学びました。いくつかのパターンを紹介したので、ここでまとめておきましょう。
- n個のものの順列における場合の数は
$n! = n(n-1) \text{…} \times 2 \times 1$
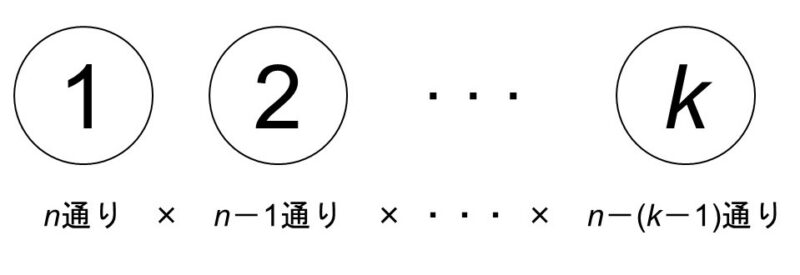
- n個のものからk個選んで順列を作る時の場合の数は
$\begin{align}
{}_n \mathrm{P}_k & = n(n-1) \text{…} (n-(k-1))\\[1.5ex]
& = \dfrac{n!}{(n-k)!}
\end{align}$
- 区別できないものを含む順列では、区別をつけて場合の数を数えた後、区別をなくす（重複している分で割る）ことで本来の場合の数を求める
- n個のものの円順列における場合の数は
$\dfrac{n!}{n} = (n-1)!$
- 円順列において、裏表がない場合（数珠順列）は2で割る
文字を使うことによって、場合の数を求めるためのいわゆる公式を導きましたが、大切なのはこれを覚えることではなく、なぜこの公式になるのかがわかることです。
順列を学ぶ理由は、一見すると順列の問題に見えない状況でも、その考え方を応用できることにあります。なので、便利なのは（公式が作れてしまうような）順列の考え方であって、公式はあくまでもそこから生まれたものに過ぎません。ここは注意しておきたいところです。
そういった意味で順列はシンプルでありながらとても奥が深いといえます。しっかりと理解しておきたいですね。
長くなりましたが、今回はここまでです。お疲れさまでした！
