こんにちは、まてがめです。
これまで2階にわたり、未来に起こりうる事象を予測するための道具である「確率」について学んできました。
確率は起こりうる未来を予測する上でとても役立ちますが、実はもう一つ便利な使い方があります。それが今回学ぶ期待値(きたいち)への応用です。
これを使うことで、例えば「損得のある試行」について、あらかじめその損得を見積もり、その試行を行うべきかを決めることができます。
また今回は、この期待値と関わりの深い平均(へいきん)についても合わせて学んでいきます。
期待値とは?
まずは簡単な例を見ながら、「期待値」とは何かを理解していきましょう。
ここに全部で15枚のカードがある。カードには数字が書かれていて、1のカードは5枚、2のカードは4枚、3のカードは3枚、4のカードは2枚、5のカードは1枚ある。ここからランダムに1枚取り出し、書いてある数字の分の点数がもらえることにする。
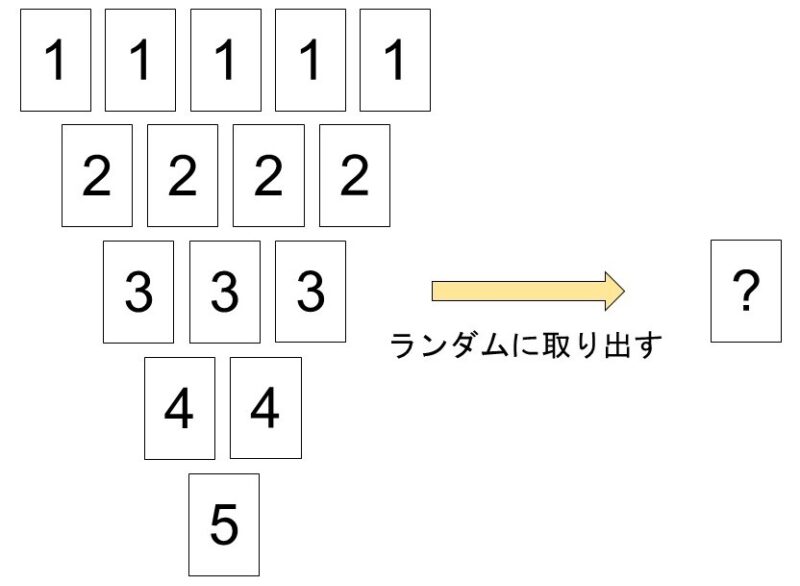
この例において、カードの数字(得点)とそれが出る確率をまとめると、次の表のようになります。
| カードの数字(得点) | 1 | 2 | 3 | 4 | 5 |
| 確率 | $\dfrac{5}{15}$ | $\dfrac{4}{15}$ | $\dfrac{3}{15}$ | $\dfrac{2}{15}$ | $\dfrac{1}{15}$ |
ここで、期待値(きたいち)という量を考えることができます。期待値とは「試行による結果として、それに応じた値がある場合、どのくらいの値となることが期待できそうか」を表す量で、英語ではExpectationと呼ぶため、頭文字のEでよく表されます。
今回の例では、期待値を計算することで「カードを取り出す試行を行った時、どのくらいの点を得ることが期待できそうか」を調べることができます。
期待値$E$は一般に次の式で計算できます。すなわち、ある試行$\mathrm{T}$を行った時に得られる値が$X_n$($n$は自然数)である確率を$P_n$とすると、
$E = X_1 P_1 + X_2 P_2 + \text{…} + X_n P_n$
となります(×の記号は省略)。各値にその出やすさ(確率)を掛け合わせて足しあげれば、得られる値がどのくらいになるか予測できるというわけです。式を見ただけでは少しわかりにくいと思うので、今回の例を使って期待値を計算してみましょう。
$\begin{align}
& \hspace{13pt} 1 \times \dfrac{5}{15} + 2 \times \dfrac{4}{15} + 3 \times \dfrac{3}{15} + 4 \times \dfrac{2}{15} + 5 \times \dfrac{1}{15} \\[1.5ex]
& = \dfrac{1 \times 5 + 2 \times 4 + 3 \times 3 + 4 \times 2 + 5 \times 1}{15} \\[1.5ex]
& = \dfrac{35}{15} \\[1.5ex]
& = \dfrac{7}{3} = 2.33 \text{…}
\end{align}$
つまり「この試行を行えば、2点ぐらい(もしくはそれ以上)の得点が期待できそうだ」ということがわかります。期待値はあくまで計算値なので、いつも自然数で求まるわけではない(分数・小数になる場合もある)ことに注意してください。
期待値と平均
この期待値という量ですが、実は平均(へいきん)と呼ばれる量と深いかかわりがあります。そこで、「平均」についても簡単な例を通して学んでおきましょう。
20人の生徒にある数学のテストを受けてもらった。問題は全部で5問あり、結果は次のようになった。
| 正解数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 2 | 3 | 7 | 5 | 2 | 1 |
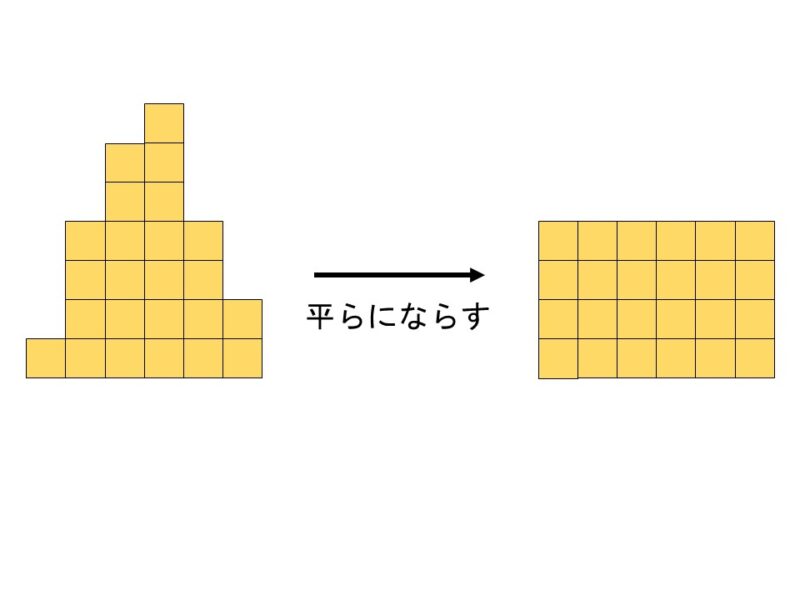
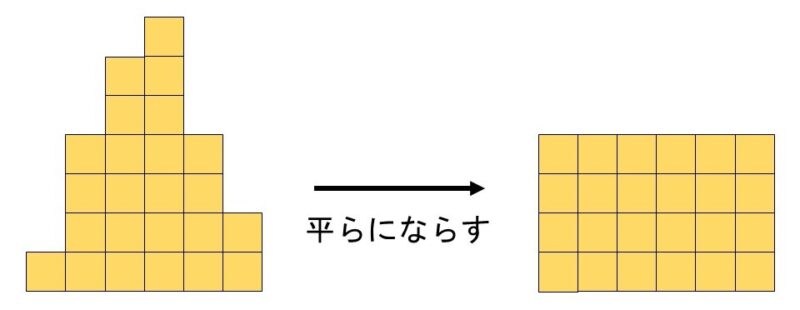
この結果から平均という量を計算してみます。平均とは「人やものが持っている値をすべて足し合わせて等しく分けた時にどのくらいの値になるか」を表す量で、集団全体としての傾向を見るためによく使われています。図のように、バラバラに積みあがったブロックを「平らにならす」イメージを持つとわかりやすいでしょう。
今回の例における平均は「生徒全体で見た時、生徒1人当たりの正解数はどのくらいか」を表しますから、全員分の正解数を足し合わせ、その人数で割ることで求めることができます。
$\begin{align}
& \hspace{13pt} \dfrac{0 \times 2 + 1 \times 3 + 2 \times 7 + 3 \times 5 + 4 \times 2 + 5 \times 1}{20} \\[1.5ex]
& = \dfrac{45}{20} \\[1.5ex]
& = \dfrac{9}{4} = 2.25
\end{align}$
したがって正解数の平均は2.25、つまり「生徒全体で見ると2問くらいは解けた」とわかるわけです。
ところでこの式、見覚えがありませんか?実は期待値の計算でも、通分した時に同じ形の式になっていました。得点の期待値を計算した時の式をもう一度見てみましょう。
$\begin{align}
& \hspace{13pt} 1 \times \dfrac{5}{15} + 2 \times \dfrac{4}{15} + 3 \times \dfrac{3}{15} + 4 \times \dfrac{2}{15} + 5 \times \dfrac{1}{15} \\[1.5ex]
& = \dfrac{1 \times 5 + 2 \times 4 + 3 \times 3 + 4 \times 2 + 5 \times 1}{15} \\[1.5ex]
& = \dfrac{35}{15} \\[1.5ex]
& = \dfrac{7}{3} = 2.33 \text{…}
\end{align}$
すなわち期待値と平均は、その意味合いこそ異なりますが、数式的には同じものであると考えることができます。実際、先ほどの例で示した「カードを取り出す試行」を繰り返し行って得点を記録していき、その平均を計算すると期待値($ \frac{7}{3} = 2.33 \text{…} $)に近づくことがわかります。
期待値を使って損得を見積もる
期待値の便利なところは、「損得がある試行を行うべきか」や「損得がどの程度になりそうか」をあらかじめ見積もることができる点にあります。次のようなものが良い例です。
Aさんは今、コインを使って遊べるゲームセンターに来ており、あるスロットゲームに挑戦しようとしている。
このゲームは、1~3でランダムに変わる3つの数字をボタンを押して止め、出た数字に応じてコインがもらえるというものである。

ただしコースが2つあるため、Aさんはどちらのコースで挑戦しようか迷っている。この時、Aさんはどちらのコースを選ぶべきか?
(1) スタンダードコース(消費コイン:3枚)
- 数字が1つもそろわない → 0枚
- 数字が1ペアそろう → その数字分の枚数
- 数字がすべてそろう → 6枚
(2) チャレンジコース(消費コイン:5枚)
- 数字が1つもそろわない → 0枚
- 数字が1ペアそろう → 6枚
- 数字がすべてそろう → 12枚
単に見比べるだけでは難しいですが、期待値を求めるとこれがわかります。それぞれのコースについて、もらえるコインの枚数の期待値を計算してみましょう。
(1) スタンダードコース(消費コイン:3枚)
起こりうるパターンについて整理してみると、次のようになりますね。
| 数字 | もらえるコインの枚数 | 場合の数 | 確率 |
| 1つもそろわない | 0 | $6 (= 3!)$ | $\dfrac{6}{27}$ |
| 1が1ペアそろう | 1 | $6 (= {}_3 \mathrm{C}_2 \times 2)$ | $\dfrac{6}{27}$ |
| 2が1ペアそろう | 2 | $6 (= {}_3 \mathrm{C}_2 \times 2)$ | $\dfrac{6}{27}$ |
| 3が1ペアそろう | 3 | $6 (= {}_3 \mathrm{C}_2 \times 2)$ | $\dfrac{6}{27}$ |
| すべてそろう | 6 | 3 | $\dfrac{3}{27}$ |
よって、もらえるコインの枚数の期待値は
$\begin{align}
& \hspace{13pt} 0 \times \dfrac{6}{27} + 1 \times \dfrac{6}{27} + 2 \times \dfrac{6}{27} + 3 \times \dfrac{6}{27} + 6 \times \dfrac{3}{27} \\[1.5ex]
& = \dfrac{54}{27} = 2
\end{align}$
一方で消費するコインは3枚ですから、このコースはコインを損する可能性が高いと考えられます。
(2) チャレンジコース(消費コイン:5枚)
こちらについても起こりうるパターンについて整理してみます。
| 数字 | もらえるコインの枚数 | 場合の数 | 確率 |
| 1つもそろわない | 0 | $6 (= 3!)$ | $\dfrac{6}{27}$ |
| 1ペアそろう | 6 | $18 (= {}_3 \mathrm{C}_2 \times 2 \times 3)$ | $\dfrac{18}{27}$ |
| すべてそろう | 12 | 3 | $\dfrac{3}{27}$ |
よって、もらえるコインの枚数の期待値は
$\begin{align}
& \hspace{13pt} 0 \times \dfrac{6}{27} + 6 \times \dfrac{18}{27} + 12 \times \dfrac{3}{27} \\[1.5ex]
& = \dfrac{144}{27} \\[1.5ex]
& = \dfrac{16}{3} = 5.33 \text{…}
\end{align}$
一方で消費するコインは4枚ですから、このコースはコインを得する可能性が高いと考えられます。
したがってAさんは、消費するコインが多いとしても(2)を選ぶべきであるといえます。
このように、損得がかかわるようなものについては、確率から期待値を求めることで、その判断に役立てることができます。
まとめ
今回は期待値と平均について学びました。内容を簡単にまとめておきます。
- ある試行$\mathrm{T}$において、確率$P_n$で値$X_n$が得られるとする($n$は自然数)。この時、期待値$E$は次の式で求めることができる。
$E = X_1 P_1 + X_2 P_2 + \text{…} + X_n P_n$
- 期待値と平均は数式の上では同じものである。
- 期待値を計算することで、「どのくらいの損得があるか」を見積もることができる。
期待値は、今回示した例のように、身の回りで起こりうる場面で役立つ考え方ですが、理学においても大切な考え方です。例えば化学では、元素の重さを計算するのに利用します。ぜひ覚えておきましょう。
今回はここまでです。お疲れさまでした!