こんにちは、まてがめです。
ここまで4階にわたり、場合の数の数え方を学んできました。
これらの方法を上手く使うことで、いろいろな状況に対して「どんなことが起こりえるのか・どんな選択肢があるのか?」や「場合の数としては何パターンあるのか?」を知ることができるわけです。
そしてなんと、このような情報から「ある物事が起こる可能性はどのくらいあるのか?」といった未来について予測を立てることもできるようになります!それが今回学ぶ確率(かくりつ)と呼ばれるものです。
確率とは?
確率(かくりつ)とは「ある物事が起こる可能性」を表します。例えば、Aという物事が起こる確率を$P(A)$(確率を表す英語Probabilityの頭文字)で表すことにすると、$P(A)$は場合の数を使った分数として次のように計算されます。
$P(A) = \dfrac{\text{Aが起こる場合の数}}{\text{起こりうるすべての場合の数}}$
確率をなぜ分数で表すかというと、割合の考え方を基にしているからです。つまり、確率は「起こりうるすべての場合の数のうち、Aが起こる場合の数がどのくらいの割合を占めているのか?」という形で表されるということです。確かに、「場合の数として全体に占める割合が大きいほど、それが起こる可能性も高い」というのは納得ですね。
では、例を通して確率への理解を深めていきましょう。
例1 コイントス
今Aさんは表裏が区別できるコインを1枚持っており、Bさんに「これを3回投げた時に表が何回出るか予想してほしい」と言ってきた。
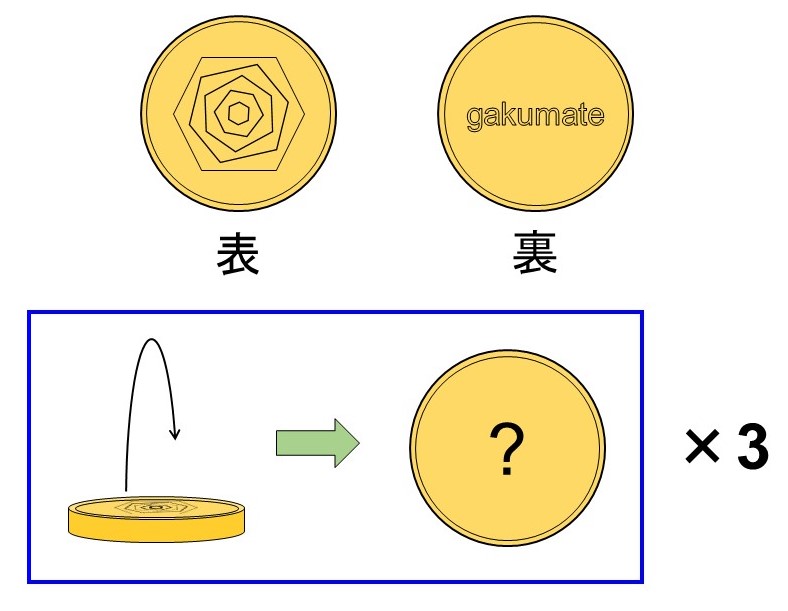
そこでBさんは、予想を的中させるべく、表が出る回数ごとに確率を計算してみることにした。
それでは、Bさんになったつもりで表が出る回数ごとにその確率を求めてみましょう。確率を求めるには、場合の数を把握しておく必要があるので、まずは計算に必要な場合の数を求めます。
[1] 起こりうるすべて(全事象)の場合の数
1~3回目のそれぞれにおいて、表が出るか裏が出るかの2通りなので、
$2 \times 2 \times 2 = 8$
すなわち、8通りです。樹形図にしてみるとわかりやすいですね。
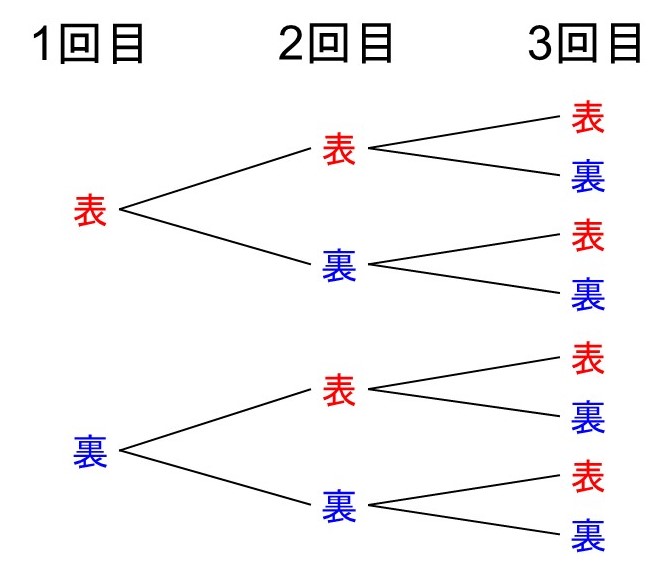
[2] 表が出ない場合の数
これは1~3回目の全てで裏となる場合なので、1通りしかありません。
[3] 表が1回出る場合の数
表が1回出るということは、残り2回は裏が出ます。つまりこれは、「3つの場所から1つを選ぶ場合の数」として考えることができます。
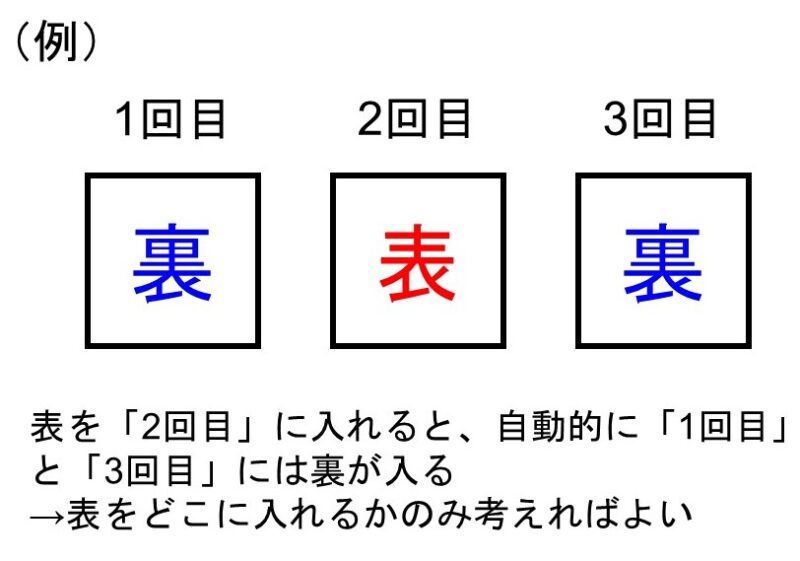
したがって、
${}_3 \mathrm{C}_1 = 3$
すなわち、3通りです(樹形図から数えてもOKです)。
[4] 表が2回出る場合の数
表が2回出るということは、残り1回は裏が出ます。よってこれは、「3つの場所から2つを選ぶ場合の数」として考えることができます。
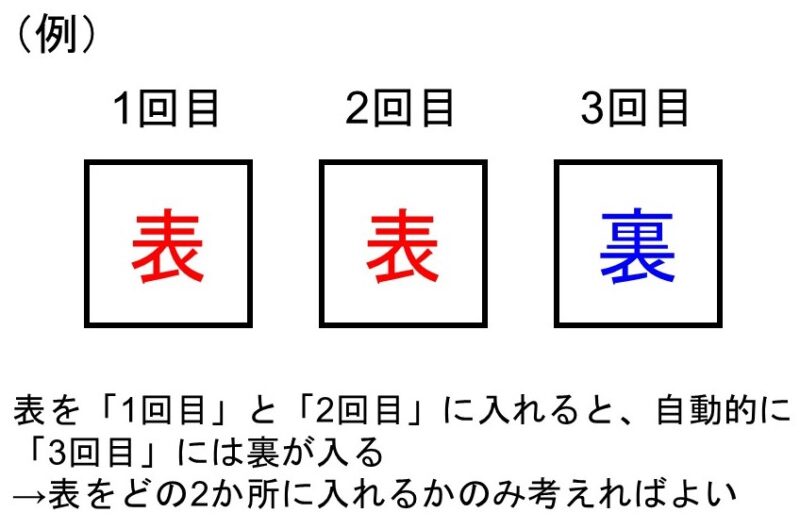
したがって、
${}_3 \mathrm{C}_2 = \dfrac{3 \times 2}{2 \times 1} = 3$
すなわち、3通りです(樹形図から数えてもOKです)。
[5] 表が3回出る場合の数
これは1~3回目の全てで表となる場合なので、1通りしかありません。
以上をまとめると、次のようになります。
| 表が出る回数 | 0 | 1 | 2 | 3 | 合計 |
| 場合の数 | 1 | 3 | 3 | 1 | 8 |
これを使って回数ごとの確率を計算してみましょう。今回の場合は、次のような分数で表せます。
$\dfrac{\text{表が○回出る場合の数}}{\text{全事象の場合の数}}$
| 表が出る回数 | 0 | 1 | 2 | 3 |
| 確率 | $\dfrac{1}{8}$ | $\dfrac{3}{8}$ | $\dfrac{3}{8}$ | $\dfrac{1}{8}$ |
よってBさんは、「表が1回出る」もしくは「表が2回出る」と予想すれば、その予想が当たる可能性は高いということになります。
例2 玉の取り出し
「確率を求めるには、場合の数がわかればよい」ということは理解できたかと思います。したがって、「いかに場合の数を上手く数えるか」が確率を求める上で重要となります。次の例を学ぶとそれがよくわかります。
赤玉1個、黄玉4個、白玉45個の計50個の玉が入った箱がある。玉には色ごとにランクが決められており、この箱から同時に3個取り出して、出た玉のランクに応じた景品をもらうことができる。
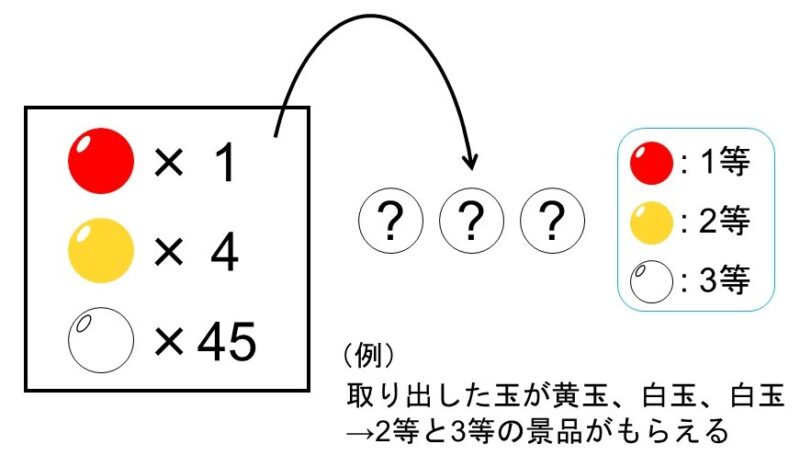
この時、次の確率はいくらになるか?
(1) 3等の景品のみがもらえる確率
(2) 2等の景品がもらえる確率
(3) 1等または2等の景品がもらえる確率
まずは、「同様に確からしい事象は何なのか」を確認しておきましょう。問題なのが「同じ色の玉を区別するのか」ということです。これについては問題文に書かれていません。
区別する(各色の玉に番号が書かれているようなイメージ)とした場合、例えば次の2つの事象は色の組合せこそ同じですが、異なる事象ということになります。
「取り出した玉が白玉1、白玉2、白玉3である」
「取り出した玉が白玉4、白玉5、白玉6である」
この2つは同様に確からしい(起こる可能性は等しい)です。
一方で区別しないとした場合、例えば次の2つの事象は果たして同様に確からしいと言えるでしょうか?
「取り出した玉が白玉、白玉、白玉である」
「取り出した玉が赤玉、赤玉、赤玉である」
箱に入っている玉の数は白玉の方が赤玉よりもずっと多いので、白玉のみを取り出す可能性の方が高いはずです。つまり、この2つは同様に確からしい事象ではありません(コイントスの例で表裏の順番を考えなかった場合と同じ話です)。
したがって、同様に確からしい事象を数えるためには、玉を区別すべきということになります。
(0) 全事象の場合の数
今回求める確率は、次のような分数として表せます。
$\dfrac{\text{条件を満たすように玉を取り出す場合の数}}{\text{3個の玉を取り出す場合の数}}$
そこで、分母となる全事象の場合の数を先に計算しておきましょう。
玉は全部で50個あり、ここから同時に3個取り出すので、「50個のものから3個を選ぶ場合の数」として計算できますね(わからない場合は22Fを確認してみてください)。
$\begin{align}
{}_{50} \mathrm{C}_3 & = \dfrac{50 \times 49 \times 48}{3 \times 2 \times 1} \\[1.5ex]
& = 19600
\end{align}$
よって、19600通りです。
(1) 3等の景品のみがもらえる確率
「3等の景品のみがもらえる」=「取り出した玉がすべて白玉」なので、この場合の数は「45個のものから3個を選ぶ場合の数」として計算できます。
$\begin{align}
{}_{45} \mathrm{C}_3 & = \dfrac{45 \times 44 \times 43}{3 \times 2 \times 1} \\[1.5ex]
& = 14190 = 2 \times 3 \times 5 \times 11 \times 43
\end{align}$
よって、求める確率は
$\begin{align}
& \hspace{13pt} \dfrac{14190}{19600} \\[1.5ex]
& = \dfrac{2 \times 3 \times 5 \times 11 \times 43}{2^4 \times 5^2 \times 7^2} \\[1.5ex]
& = \dfrac{3 \times 11 \times 43}{2^3 \times 5 \times 7^2} = \dfrac{1419}{1960}
\end{align}$
となります。
(2) 2等の景品がもらえる確率
「2等の景品がもらえる」=「取り出した玉に黄玉が含まれる」なので、この場合の数を計算するには2通りの方法が考えられます。
- 取り出す黄玉の数ごとに場合分け(取り出す黄玉が1個の時、2個の時、3個の時)
- 「全事象の場合の数」から「黄玉を取り出さない場合の数」を差し引く
1の方法は素直ですが、今回は玉の数が多いため、計算してみると少し大変です。
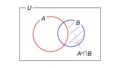
一方、2の方法は集合の考え方を基にしたものです。全事象を$U$、「取り出した玉に黄玉が含まれる」という事象をYellow(黄色)の$Y$で表すことにすると、次のようなベン図が描けます。
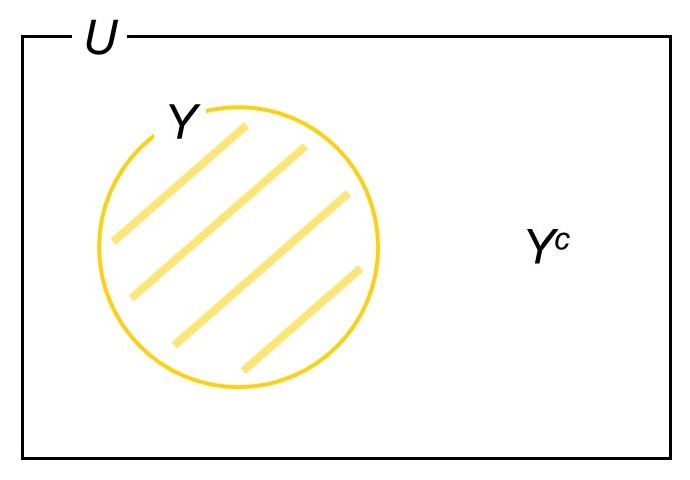
求めたいのは$Y$の個数$n(Y)$ですが、$Y$の外側である補集合$Y^c$(黄玉を取り出さない場合)に注目すると、次のような式で計算できます。
$n(Y) = n(U)-n(Y^c)$
$n(U)$はすでに計算しているので、$n(Y^c)$を計算すれば、この式から$n(Y)$が求まります。
「黄玉を取り出さない」=「黄玉以外の玉(白玉か赤玉)を取り出す」なので、$n(Y^c)$は「46個のものから3個を選ぶ時の場合の数」として計算できます。
$\begin{align}
n(Y^c)&={}_{46} \mathrm{C}_3 \\[1.5ex]
& = \dfrac{46 \times 45 \times 44}{3 \times 2 \times 1} \\[1.5ex]
& = 15180
\end{align}$
これより、$n(Y)$は次のようになります。
$\begin{align}
n(Y) & = n(U)-n(Y^c) \\[1.5ex]
& = 19600-15180 \\[1.5ex]
& = 4420 = 2^2 \times 5 \times 221
\end{align}$
よって、求める確率は
$\begin{align}
\dfrac{n(Y)}{n(U)} & = \dfrac{4420}{19600} \\[1.5ex]
& = \dfrac{2^2 \times 5 \times 221}{2^4 \times 5^2 \times 7^2} \\[1.5ex]
& = \dfrac{221}{2^2 \times 5 \times 7^2} = \dfrac{221}{980}
\end{align}$
となります。
(3) 1等または2等の景品がもらえる確率
「1等または2等の景品がもらえる」=「取り出した玉に赤玉または黄玉が含まれる」ということですが、「または」という言葉で思い出したいのが和集合です。
すなわち「取り出した玉に赤玉または黄玉が含まれる」という事象は、「取り出した玉に赤玉が含まれる」という事象と「取り出した玉に黄玉が含まれる」という事象の和集合になります。なので、「取り出した玉に赤玉が含まれる」という事象をRed(赤色)の$R$とすると、今回の事象は次のベン図に示す部分($R \cup Y$)となります。
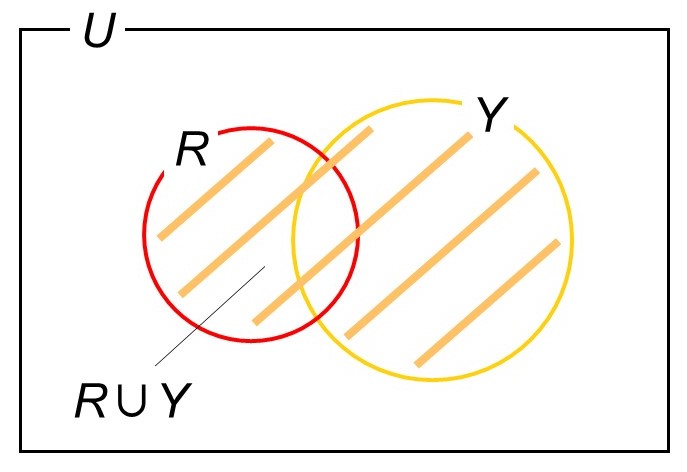
復習になりますが、和集合の個数$n(R \cup Y)$は次のように計算できます。ポイントは「それぞれの集合の個数を足してから重複分(共通部分)を差し引く」でした。
$n(R \cup Y) = n(R)+n(Y)-n(R \cap Y)$
計算に使う場合の数を計算しておきましょう。
- $n(R)$
取り出した玉に赤玉が含まれる場合、1個は1個だけ入っている赤玉から、2個は残り49個の玉から取り出すことになります。
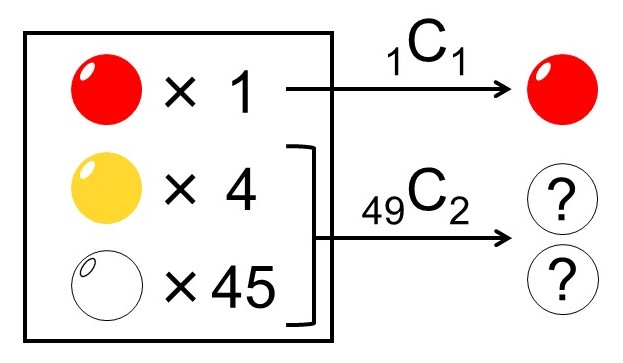
ゆえに、場合の数$n(R)$は
$\begin{align}
n(R) & = {}_1 \mathrm{C}_1 \times {}_{49} \mathrm{C}_2 \\[1.5ex]
& = 1176 = 2^3 \times 3 \times 7^2
\end{align}$
- $n(Y)$
これはすでに(2)で求めています。
$n(Y) = 4420 = 2^2 \times 5 \times 221$
- $n(R \cap Y)$
取り出した玉に赤玉と黄玉の両方が含まれる場合は、次の2通りが考えられます。
- 赤玉:1個、黄玉:1個、白玉:1個を取り出す場合
- 赤玉:1個、黄玉:2個を取り出す場合
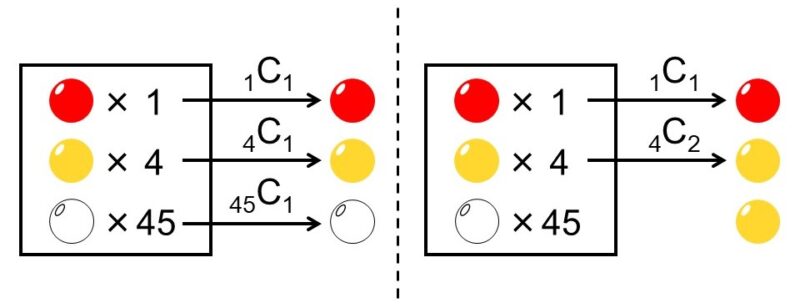
ゆえに、場合の数$n(R \cap Y)$は
$\begin{align}
n(R \cap Y) & = {}_1 \mathrm{C}_1 \times {}_4 \mathrm{C}_1 \times {}_{45} \mathrm{C}_1+{}_1 \mathrm{C}_1 \times {}_4 \mathrm{C}_2 \\[1.5ex]
& = 186 = 2 \times 3 \times 31
\end{align}$
以上より、取り出した玉に赤玉または黄玉が含まれる(=1等または2等が当たる)場合の数$n(R \cup Y)$は
$\begin{align}
& \hspace{13pt} n(R \cup Y) \\[1.5ex]
& = n(R)+n(Y)-n(R \cap Y) \\[1.5ex]
& = 1176+4420-186 \\[1.5ex]
& = 5410 = 2 \times 5 \times 541
\end{align}$
したがって、求める確率は
$\begin{align}
\dfrac{n(R \cup Y)}{n(U)} & = \dfrac{5410}{19600} \\[1.5ex]
& = \dfrac{2 \times 5 \times 541}{2^4 \times 5^2 \times 7^2} \\[1.5ex]
& = \dfrac{541}{2^3 \times 5 \times 7^2} = \dfrac{541}{1960}
\end{align}$
となります。
まとめ
今回は確率について学びました。「場合の数を割合という形で分数に表す」というシンプルな考え方ですが、未来を予測するための道具として、あらゆる分野で使われています。
これまで学んだ道具(樹形図・順列・組合せ・集合)を使って場合の数を正しく数えることさえできれば、確率を求めることは決して難しくありません。「場合の数を上手く数えられるようになる」ことが確率を得意にする近道ですよ。
今回はここまでです。お疲れさまでした!