こんにちは、まてがめです。
これまで10進法・位取り・四則演算・自然数・分数・小数について学び、「数」という理学において必要な「基本道具」を手に入れました。
この章から、もう一つ重要な要素についても手に入れていきます。それは「数を扱うための方法」です。
簡単な例を使って、その重要性を考えてみましょう。
あなたは夕方にショッピングモールに来ていて、これから洋服店・雑貨店・レストラン・食料品店に行く予定です。この時、どうやって行動を決めますか?
ここで、数を扱う方法を知らないAさんと知っているBさんで、どんな違いがあるか見てみます。
(Aさんの場合)
「4つのうちのどこから行こうかな…よし、とりあえず洋服から見よう!」
行くべきお店の数を「4つ」として認識はしていましたが、夕方なので行く順番は何でもよいというわけではないですよね。これだと途中で「時間がなくて行きたいお店に行けなかった…」と後悔するかもしれません。
(Bさんの場合)
「行き方は$4 \times 3 \times 2 \times 1$の24通りか…少し多いから条件をつけて選択肢を絞ろう。まず、レストランは一番早く閉まるから最初に行こう。買うものが一番多くて荷物が増える食料品店は最後に行った方がいいかな。となると、洋服店と雑貨店のどちらから行くかの2通りだけ考えればいいってことか。時間をかけて見たいのは洋服の方だから、レストラン → 洋服店 → 雑貨店 → 食料品店の順に行こう。」
このように、数を扱うための方法が身についていると、必要な計算と論理を用いてベストな判断ができます。だからこそ、方法は道具と同じくらい大切なんです。
では、「数を扱う方法」の基本を身につけるために何を学ぶ必要があるかというと、2つあります。
- 場合の数と確率
- 図形(次の章で学びます)
この章で学んでいく場合の数と確率という単元は、主に「物事において何が起こりうるのかをあらかじめ知るため」に必要なものとなります。Bさんはこれをうまく使っていました。
今回はその基礎となる考え方、樹形図(じゅけいず)について学びます。
樹形図
例1 コイントス
次のような例について考えてみましょう。
ここに表と裏が区別できる1枚のコインがある。今からこれを2回投げ、出た面を確認する。
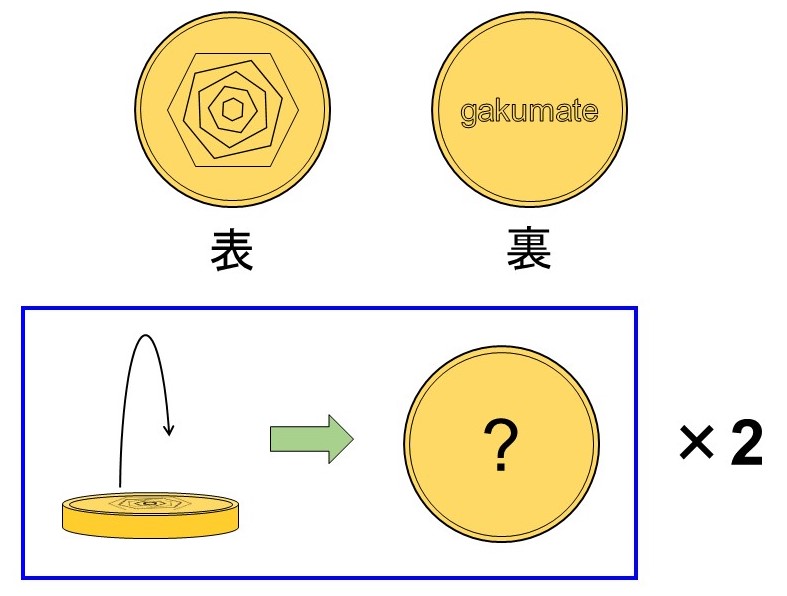
この時、起こりうる場合は何通りあるか?
1回目と2回目のそれぞれで表と裏が出る可能性があるので、いくつかのパターンが考えられそうですね。
場合の数をもれなく数える時は図を描いてみるとわかりやすいのですが、その際に便利なのが樹形図(じゅけいず)と呼ばれる図です。これはその名の通り、木の枝のように起こりうる場合を書き出して描く図になります。
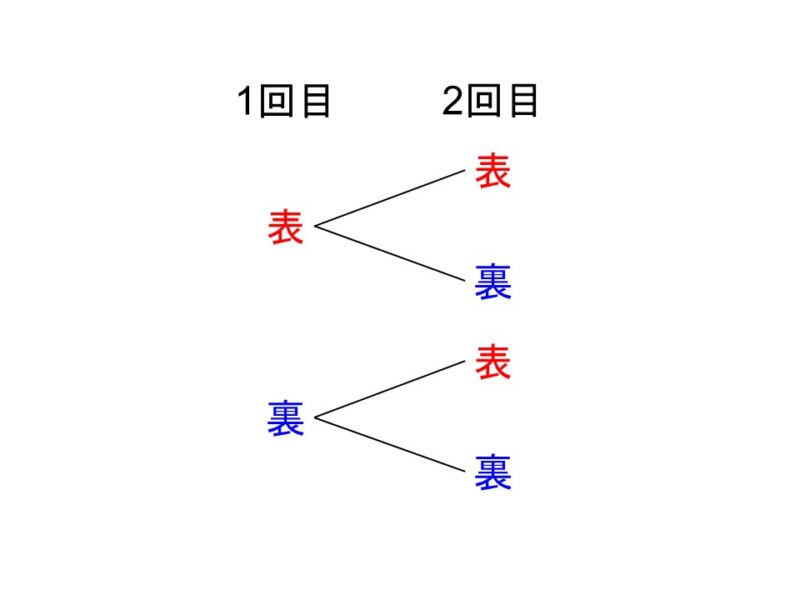
今回の例では、次のような樹形図を描くことができます。
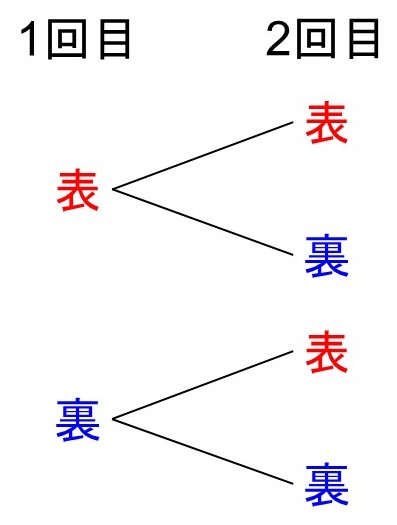
ポイントとしては、最初に起こりうる場合を縦に書き出し、それを起点にして次に起こりうる場合を縦に枝分かれで書いていきます。樹形図を作ることで「どんな場合が考えられるか」や「場合の数が何通りあるか」をもれなく確認することができます。
樹形図から、起こりうる場合の数は
(表→表) (表→裏) (裏→表) (裏→裏)
の4通りであることがわかります。
例2 色の異なる玉の取り出し
次のような例ではどうでしょうか?
ここに袋があり、袋にはそれぞれ赤、青、黄、緑の4色で塗られた玉が4個入っている。ここから1個ずつ順番に玉を取り出していき、何回目に何色が出たかを確認する。
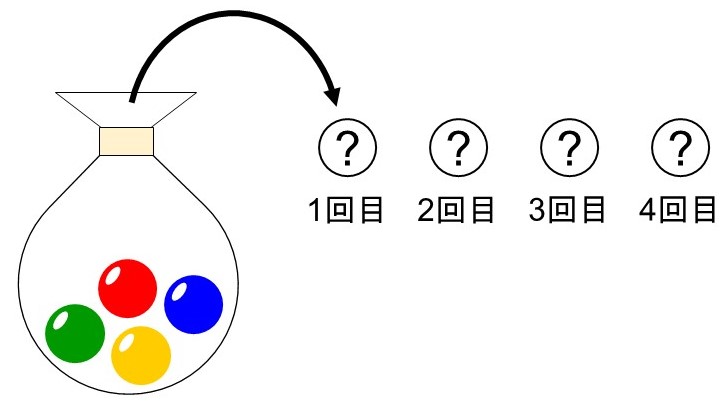
この時、3回目に青玉を取り出す場合は何通りあるか?
先ほどのコインの例よりも考えられる場合が多いので、頭の中で数えるのは難しそうです。こんな時は樹形図を描いてみましょう。
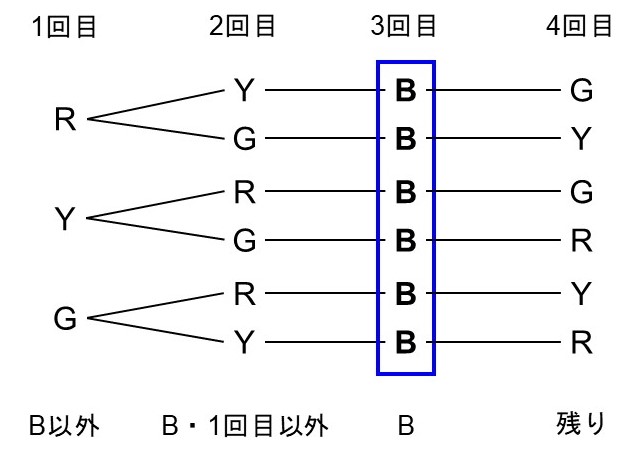
赤玉=R(Red)、青玉=B(Blue)、黄玉=Y(Yellow)、緑玉=G(Green)として樹形図を描くと次のようになります。
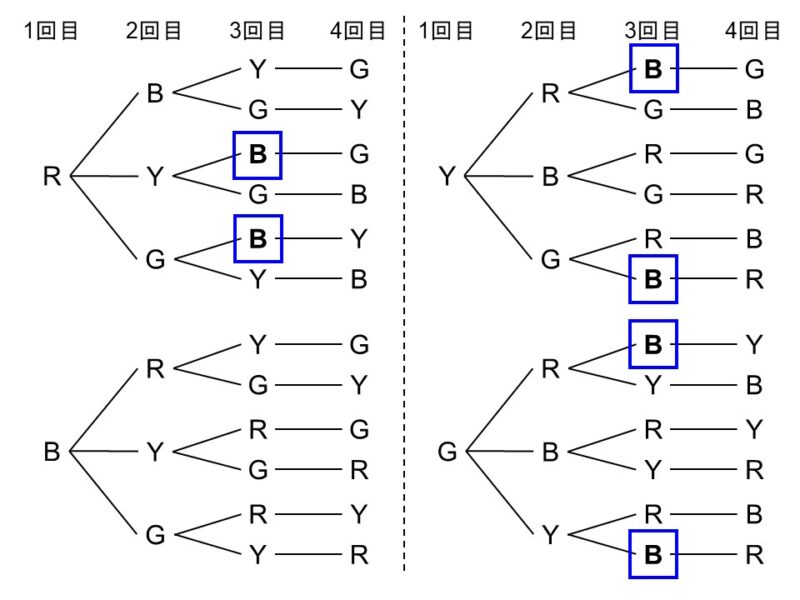
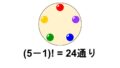
起こりうる場合の数は全部で24通りです。その中で3回目に青玉(B)が来ているものを数えると、
(R→Y→B→G) (R→G→B→Y) (Y→R→B→G)
(Y→G→B→R) (G→R→B→Y) (G→Y→B→R)
の6通りであることがわかります。
例3 数を作る
もう一つ例を考えてみましょう。
1~5の数字が書かれた5枚のカードがある。ここから2枚のカードを取り出し、
(十の位) < (一の位)
となるように2桁の数を作ることにした。
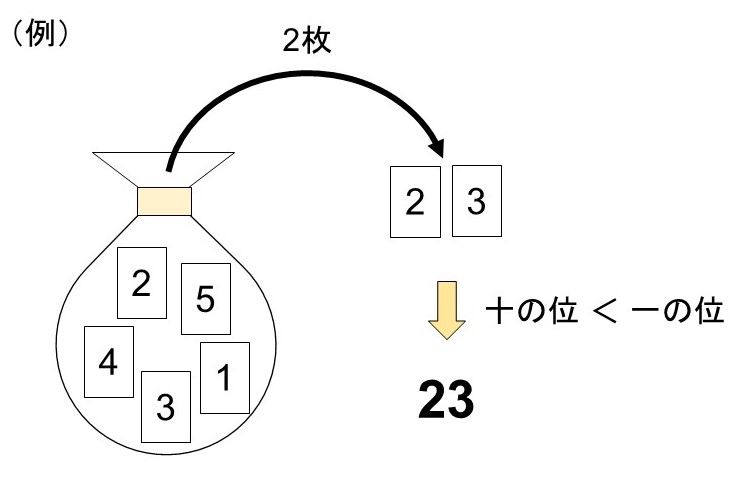
この時、3の倍数(3で割り切れる数)ができる場合は何通りあるか?
今回は(十の位) < (一の位)という条件がついているので、これに注意して樹形図を作ってみましょう。
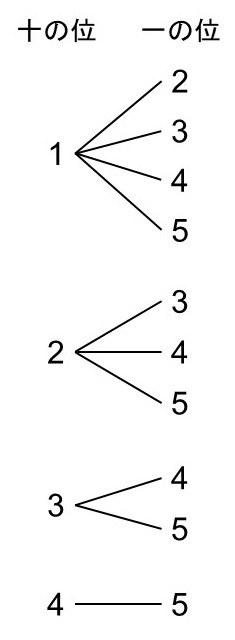
よって、作れる数は全部で10通りとなります。
さて、3の倍数の見分け方は覚えていますか?復習しておくと、ある数が3の倍数である時、各位の数を足すとそれが3の倍数になります(倍数の見分け方についての解説はこちら)。樹形図の隣に各位の和を書き出してみましょう。
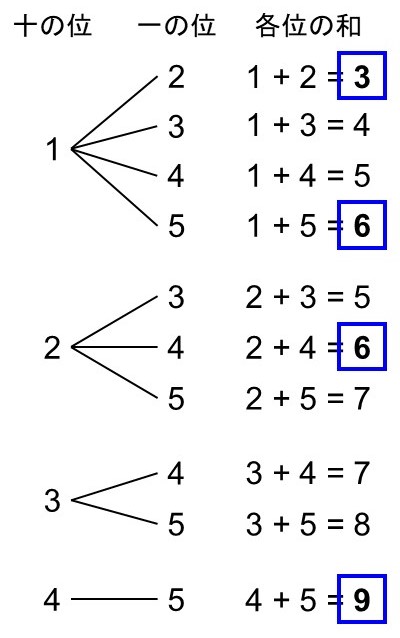
したがって、12, 15, 24, 45の時に3の倍数となるので、4通りが答えとなります。
まとめ
今回は樹形図について学びました。もちろん、場合の数が増えてくると手間はかかりますが、「確実」かつ「もれなく」場合を数えることができる方法であるため、上手く数える方法が思いつかない時はまず樹形図を作ることをオススメします。
今回はここまでです。お疲れさまでした!