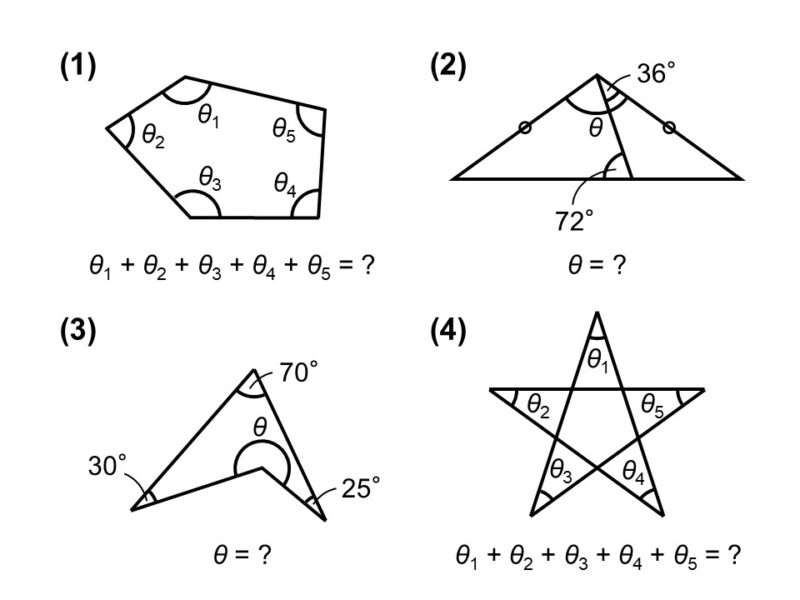
今回の問題はこちらです。（※30Fまでの内容を理解していることが前提です！）
次の？に入る角度を求めなさい。
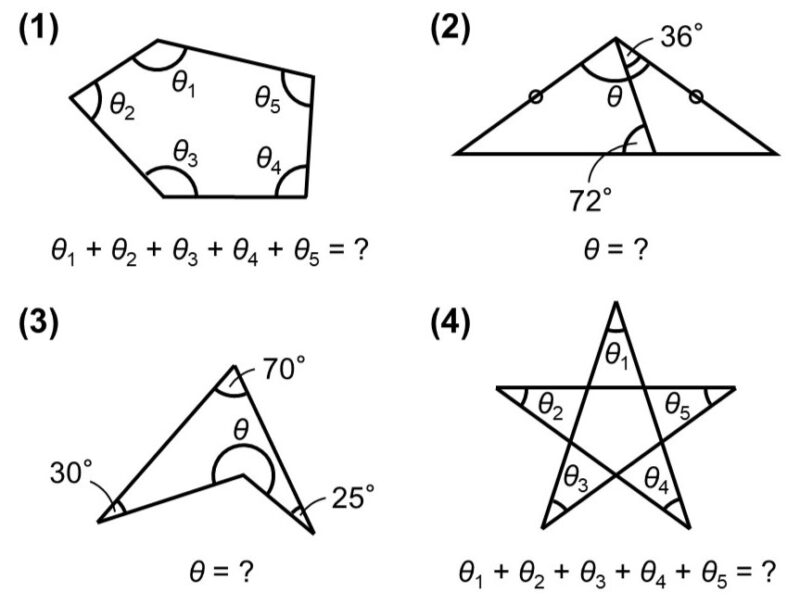
「角度の扱い方に慣れる」ことが今回のテーマです。
(1) 多角形は三角形の集まり
(1)は五角形の内角の和を求める問題です。説明しやすくするため、頂点に記号をふっておきます。
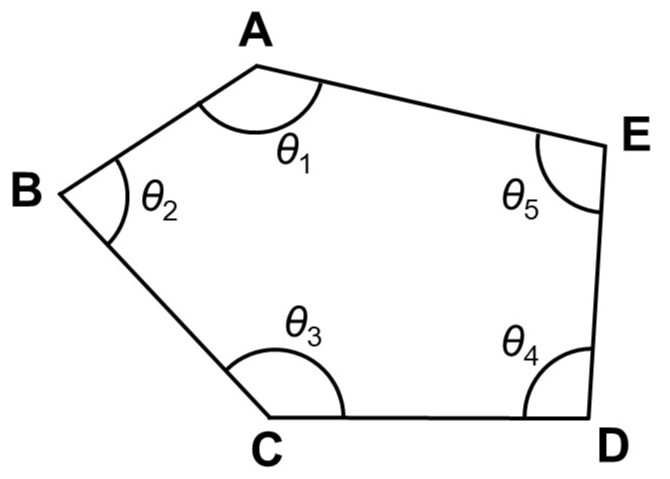
確かにこのまま和を求めるのは難しいです。そこで「多角形は必ず三角形に分けることができる」という多角形の性質を使って、考えやすくしてみましょう。
例えば、$\mathrm{A}$から対角線を引いてみると、この五角形は3つの三角形（$\triangle \mathrm{ABC}$, $\triangle \mathrm{ACD}$, $\triangle \mathrm{ADE}$）に分けることができます。
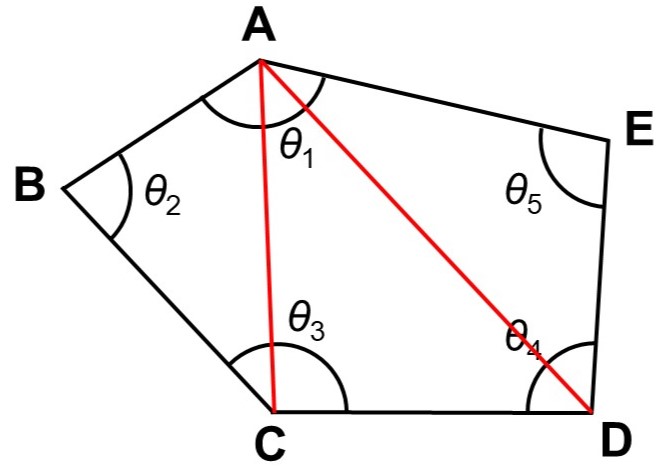
三角形の内角の和は180°でしたから、求める内角の和は
$\begin{align}
\theta_{1}+\theta_{2}+\theta_{3}+\theta_{4}+\theta_{5} &= 180^{\circ} \times 3 \\[1.5ex]
&= 540^{\circ}
\end{align}$
となります。
(2) 外角と二等辺三角形をうまく使おう
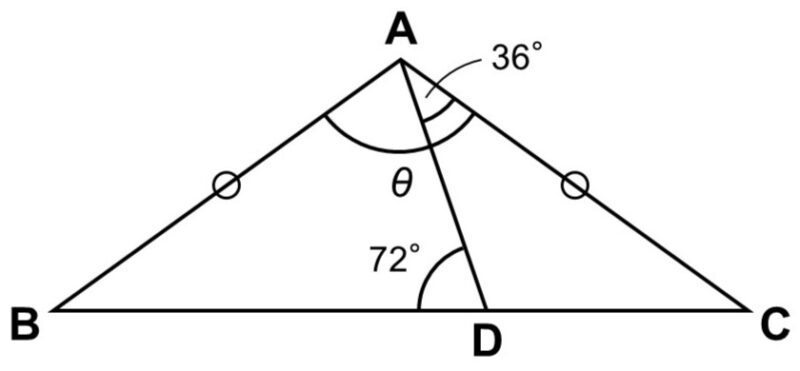
今はわかっている角が2つあるので、まずはこの2つに関わりがありそうな$\triangle \mathrm{ADC}$に注目してみます。
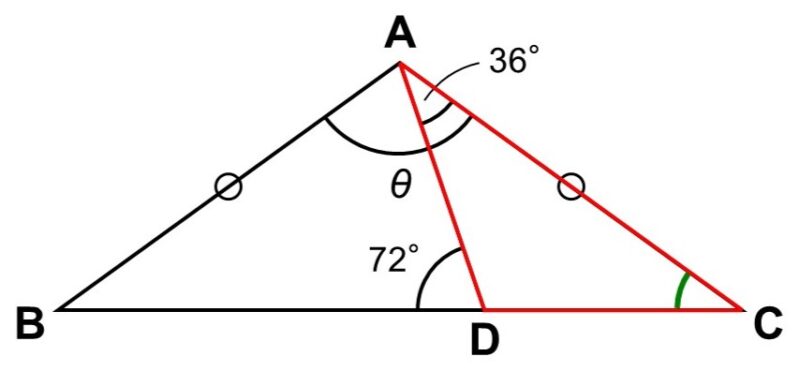
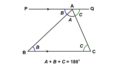
$\angle \mathrm{ADB}(= 72^{\circ})$は$\triangle \mathrm{ADC}$の外角であり、隣り合わない内角の和に等しくなりますから、
$\begin{align}
\angle \mathrm{ADB} &= \angle \mathrm{DCA}+\angle \mathrm{CAD} \\[1.5ex]
\iff \hspace{5pt} 72^{\circ} &= \angle \mathrm{DCA}+36^{\circ}
\end{align}$
であることがわかります（$\iff$は同値…「前後が数学的に同じ」を表す記号）。つまり、
$\begin{align}
\angle \mathrm{DCA} &= 72^{\circ}-36^{\circ} \\[1.5ex]
&= 36^{\circ}
\end{align}$
ということです。
そこで今度は$\angle \mathrm{DCA}$を内角に持つような三角形、例えば$\triangle \mathrm{ABC}$に注目してみます。
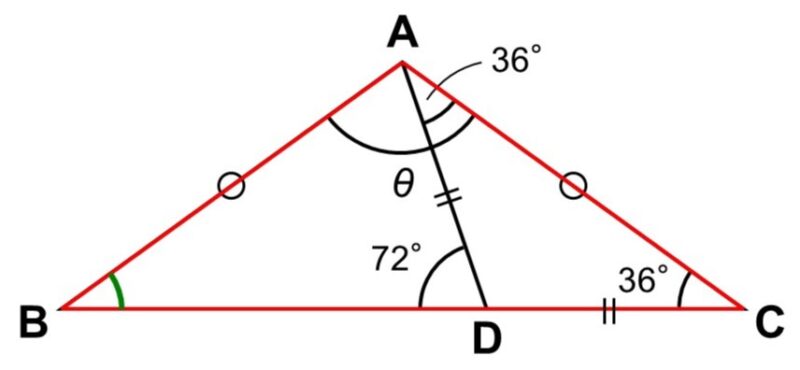
すると、$\triangle \mathrm{ABC}$は二等辺三角形であり、底角が等しいので、
$\angle \mathrm{ABC} = \angle \mathrm{ACB} = 36^{\circ}$
であることもわかります。ここまで来れば、求める角$\theta$も$\triangle \mathrm{ABC}$の内角ですから、三角形の内角の和が180°になることを使えば、
$\theta = 180^{\circ}-36^{\circ} \times 2 = 108^{\circ}$
とわかります。
(3) 基本はやっぱり三角形
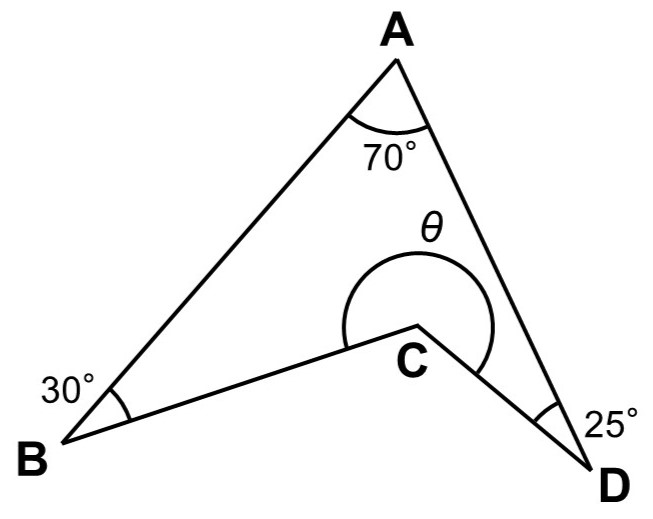
一見とっつきにくそうに見えますが、三角形に分けてしまえばこわくありません。例えば、$\mathrm{CD}$を$\mathrm{C}$の方に延ばして$\triangle \mathrm{AED}$を作ってみます。
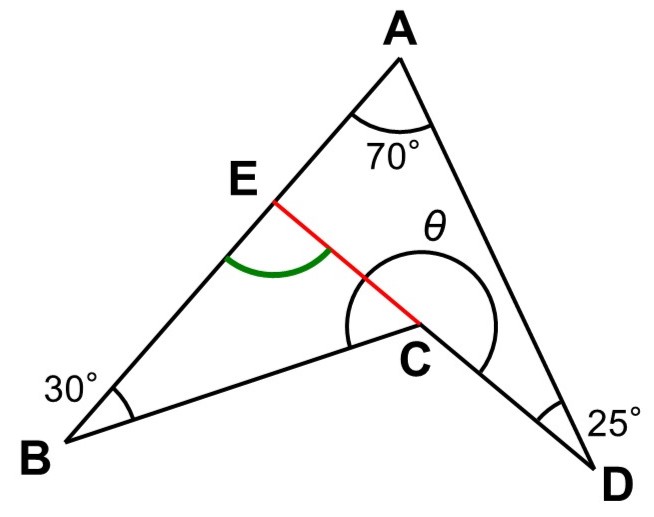
すると、今は2つの内角$\angle \mathrm{DAE}(=70^{\circ})$, $\angle \mathrm{EDA}(=25^{\circ})$がわかっていますから、外角にあたる$\angle \mathrm{DEB}$を求めることができます。
$\begin{align}
\angle \mathrm{DEB} &= \angle \mathrm{DAE}+\angle \mathrm{EDA} \\[1.5ex]
&= 70^{\circ}+25^{\circ} \\[1.5ex]
&= 95^{\circ}
\end{align}$
続いて、$\triangle \mathrm{EBC}$に注目してみます。
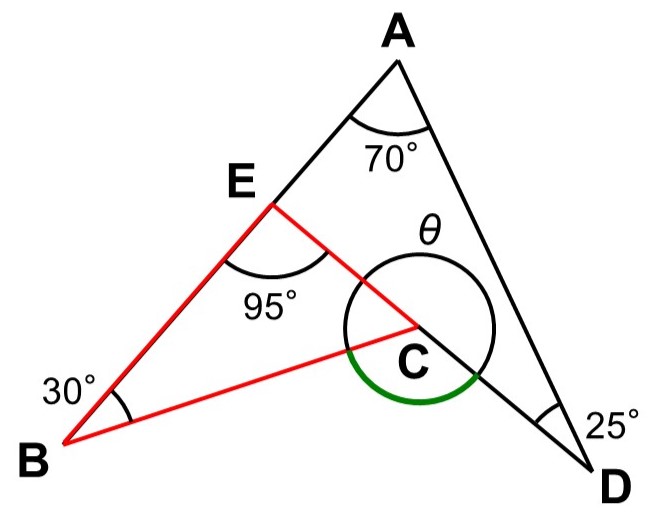
すでに$\angle \mathrm{EBC}(= 30^{\circ})$がわかっており、先ほど$\angle \mathrm{CEB}(= 95^{\circ})$もわかったので、外角にあたる$\angle \mathrm{BCD}$を求めることができます。
$\begin{align}
\angle \mathrm{BCD} &= \angle \mathrm{EBC}+\angle \mathrm{CEB} \\[1.5ex]
&= 30^{\circ}+95^{\circ} \\[1.5ex]
&= 125^{\circ}
\end{align}$
角度は1周で360°ですから、ここから$\angle \mathrm{BCD}$を差し引けば$\theta$が求まりますね。
$\begin{align}
\theta = 360^{\circ}-125^{\circ} = 235^{\circ}
\end{align}$
基本はいつでも三角形です。
(4) 散らばった角度→三角形の外角を使って集める！
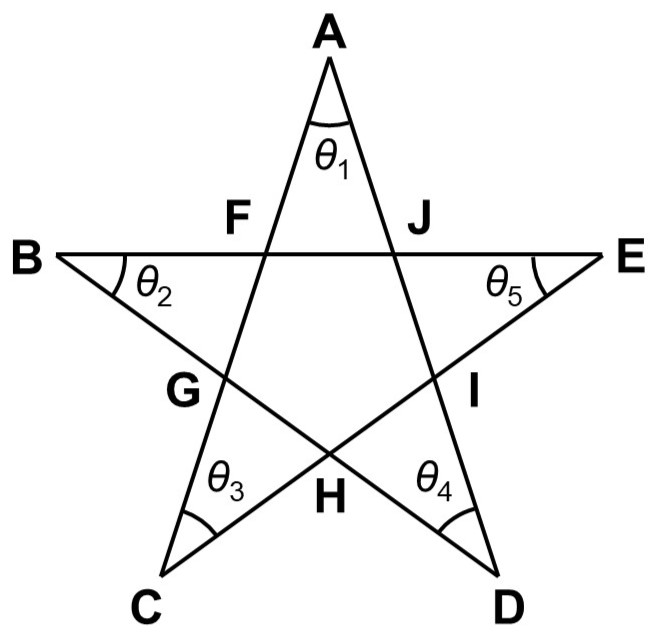
今回は三角形がたくさんあるので、これらを活用していきましょう。(2), (3)で見てきたように、外角を利用すると角度を集めることができます。
例えば、$\triangle \mathrm{ACI}$に着目すると、$\angle \mathrm{IAC}(= \theta_{1})$と$\angle \mathrm{ACI}(=\theta_{3})$を外角$\angle \mathrm{AIE}$に集めることができます。
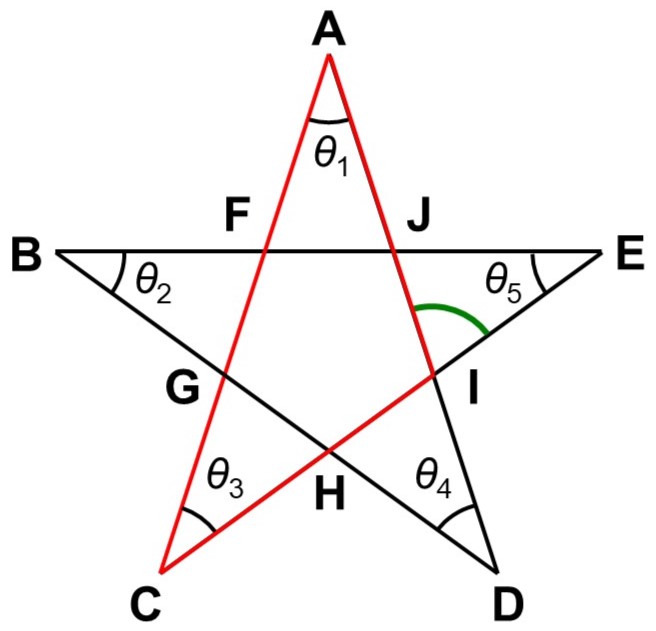
すなわち、$\angle \mathrm{AIE} = \theta_{1}+\theta_{3}$となります。
続いて、$\triangle \mathrm{JIE}$に着目すると、$\angle \mathrm{JIE}(=\theta_{1}+\theta_{3})$と$\angle \mathrm{IEJ}(=\theta_{5})$を外角$\angle \mathrm{IJB}$にまとめることができます。
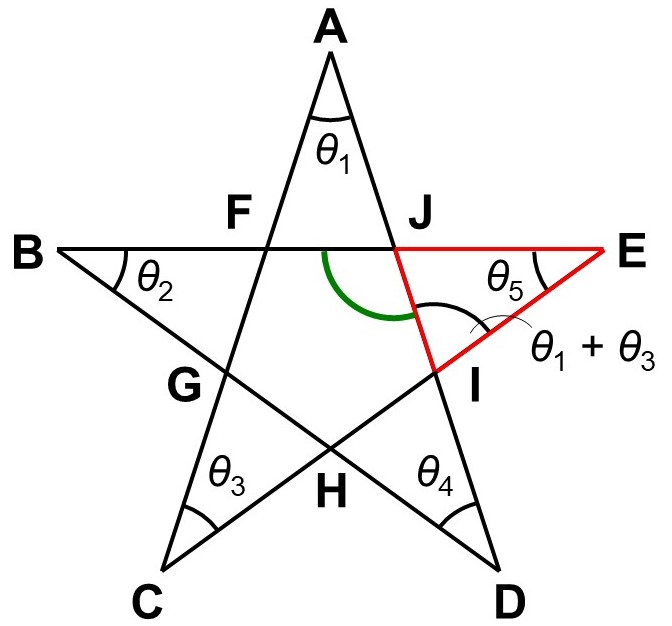
すなわち、$\angle \mathrm{IJB} = \theta_{1}+\theta_{3}+\theta_{5}$となります。
ここまで来れば、あることに気がつくはずです。それは、$\theta_{1}$, $\theta_{2}$, $\theta_{3}$, $\theta_{4}$, $\theta_{5}$の全てが$\triangle \mathrm{BDJ}$の内角として集まっているということです。
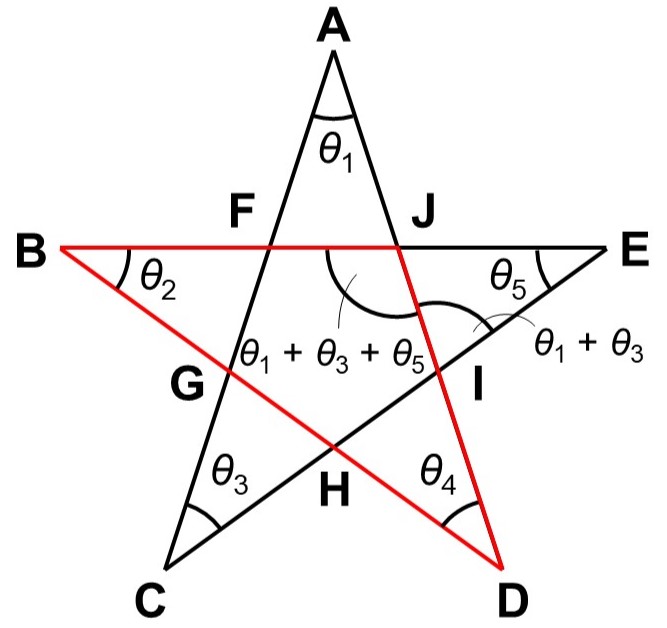
三角形の内角の和は180°なので、結局
$\theta_{1}+\theta_{2}+\theta_{3}+\theta_{4}+\theta_{5} = 180^{\circ}$
ということになります。
このように、散らばった角度を集める時は三角形の外角を利用するとうまくいくことが多いです。
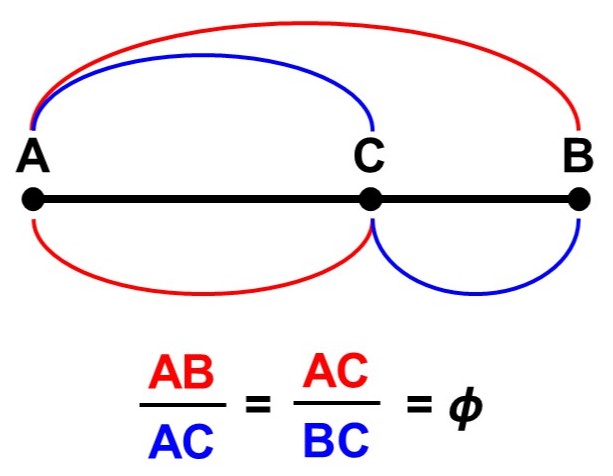
正五角形と黄金比
今回は「角度の扱い方に慣れる」というテーマで問題を作りましたが、実はもう一つのあるテーマも意識していました。それは「正五角形」です。
30Fで正三角形（3つの辺の長さ・3つの内角が等しい三角形）について紹介しましたが、正五角形は5つの辺の長さ・5つの内角が等しい五角形で、(1)の特別な場合とも言えます。
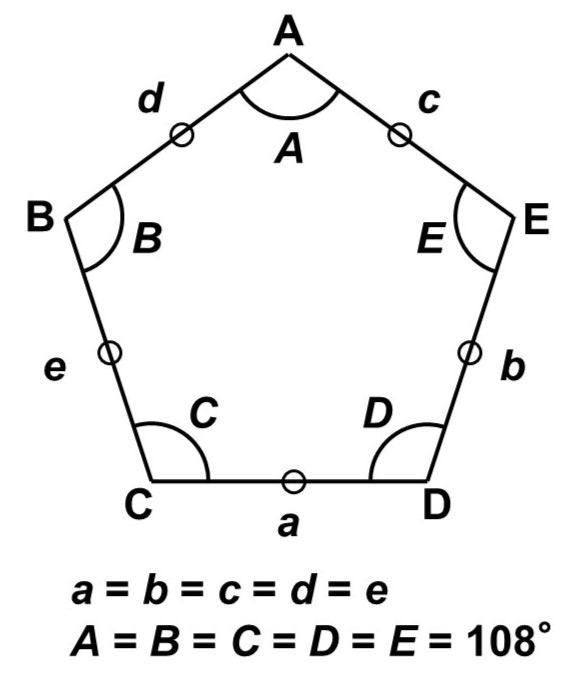
五角形の内角の和は$180^{\circ} \times (5-2) = 540^{\circ}$なので、正五角形の1つの内角の大きさは
$\dfrac{540^{\circ}}{5} = 108^{\circ}$
となります。また、正五角形の各頂点から対角線を引いてみると、(2)の二等辺三角形や(4)の星形ができることもわかりますね。
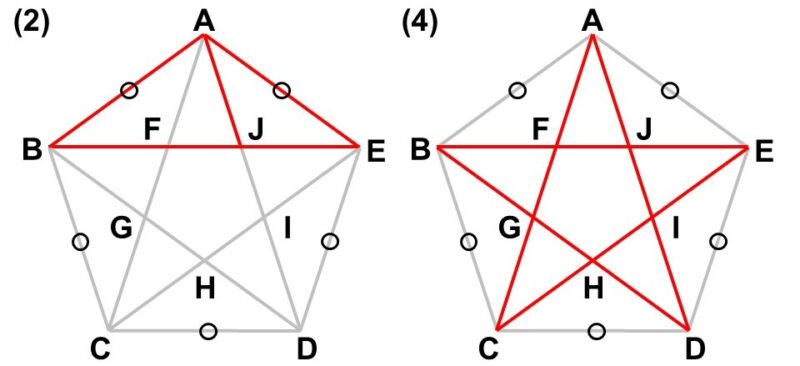
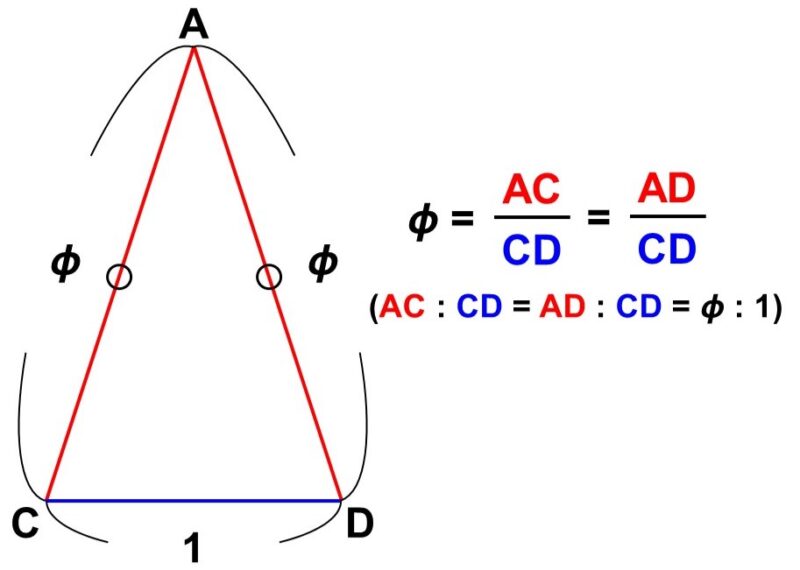
この図を見ていると、たくさんの二等辺三角形がかくれていることに気づきますが、例えば今$\triangle \mathrm{ACD}$に注目してみます。これは$\mathrm{AC} = \mathrm{AD}$の二等辺三角形なのですが、特に辺の比率$\frac{\mathrm{AC}}{\mathrm{CD}}$（辺の比$\mathrm{AC} : \mathrm{CD}$）は黄金比（おうごんひ）と呼ばれており、ギリシャ文字$\phi$（ファイ）で表されます[1]。
黄金比はヒマワリの種の配列のように自然界にたびたび顔を出す比率で、数学的に美しい比率であると言われることもあります。そのため、ギリシャの世界遺産であるパルテノン神殿をはじめとする建築や芸術作品などに利用されてきました[2]。
黄金比の定義については、平面図形の学問を体系的にまとめたことで有名なユークリッドが次のような形で定めています[2]。
「黄金比$\phi$とは、線分$\mathrm{AB}$が点$\mathrm{C}$によって分けられている（内分されている）時、
$\dfrac{\mathrm{AB}}{\mathrm{AC}} = \dfrac{\mathrm{AC}}{\mathrm{BC}}$
となるような比率である。」
では、黄金比$\phi$がいくつなのかというと、
$\phi = 1.618033…$
となっており、これまでに学んでいる自然数や分数を使って簡単に表すことはできません（この先で学ぶ「ルート」の知識が必要）。しかし、T2で紹介した「無限に続く連分数」を使うと、次のようなシンプルな形で表せます[1], [2]。
$\phi = 1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\text{…}}}}$
実際に計算してみると、分母を下にのばしていくほど$\phi$に近づいていくことがわかります。興味がある方は、ぜひ試してみてください。
参考資料
[1] Newton別冊 科学の発展に欠かせない, 「2乗してマイナスになる数」 虚数がよくわかる 改訂第3版 (礒田正美, 木村俊一, 小谷善行, 小山信也, 和田純夫 / ニュートンプレス 2022)
[2] ビジュアルガイド もっと知りたい数学 深遠なる「幾何学」の世界 (マイク・ゴールドスミス (訳: 緑慎也) / 創元社 2021)
