こんにちは、まてがめです。
前回は平面図形の基礎である「三角形」について、その基本的な性質を学びました。
- 30F 「三角形が持つ性質とは?」 ― 三角形の内角の和・辺と角の関係・成立条件
この階でも引き続き、三角形について学んでいきます。今回のテーマは「どうすれば同じ三角形が作れるか?」です。
この問い、一見とてもシンプルですが、実は奥が深いんです。というのも、これがわかるようになると、元の図形と同じ図形が作れるようになることはもちろん、様々な図形についてより多くの情報を得ることもできるようになるからです。
特に後者の使い方は、これから平面図形を学んでいく中でよく出てくるので、この階でしっかり押さえておきましょう!
「合同」とは?
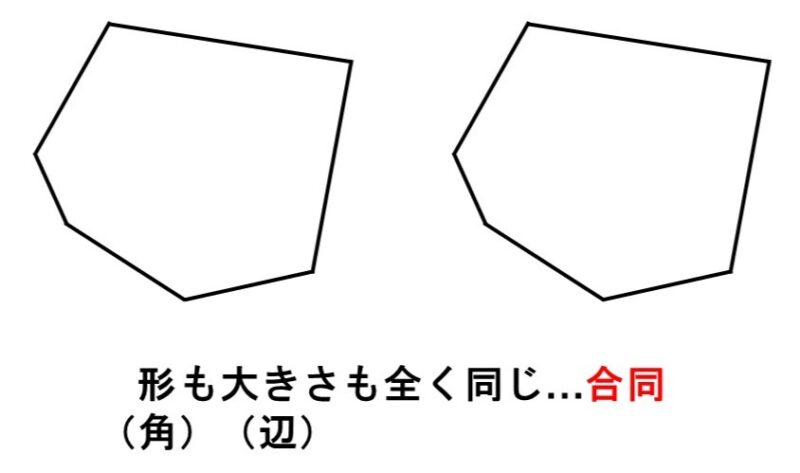
2つの図形があり、形も大きさも全く同じで、重ね合わせた時にぴったり一致するとします。この時、2つの図形は合同(ごうどう)であるという言い方をします。
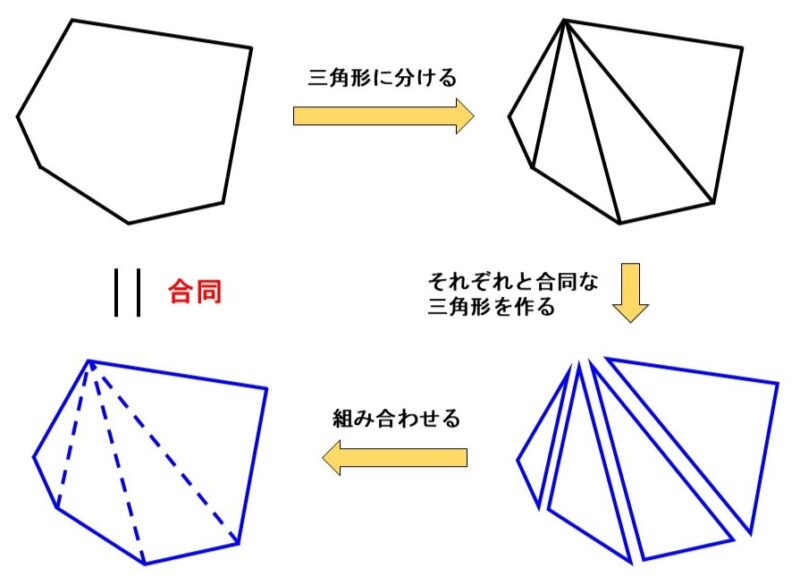
前回説明したように、多角形は三角形に分けることができます。なので、もし合同な図形を作りたいのであれば、それをいくつかの三角形に分け、それぞれと合同なものを作って組み合わせればよいことになります。
ということは結局、「どうやって合同な三角形を作ればよいのか」がわかれば、あらゆる合同な図形が作れると言えます。
三角形が合同であるために必要な条件は?
では、三角形はどのような時に合同(=形も大きさも同じ)になるのでしょうか?
確かに「3辺の長さ」と「3つの内角の大きさ」が同じであれば、間違いなく合同な三角形だと言えます。しかしこれでは要素が6つも必要なので、少しめんどうです。
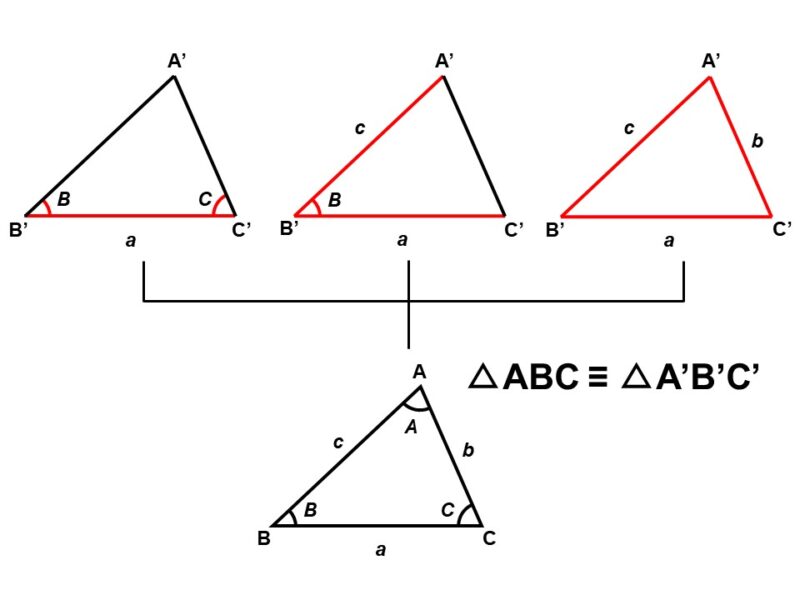
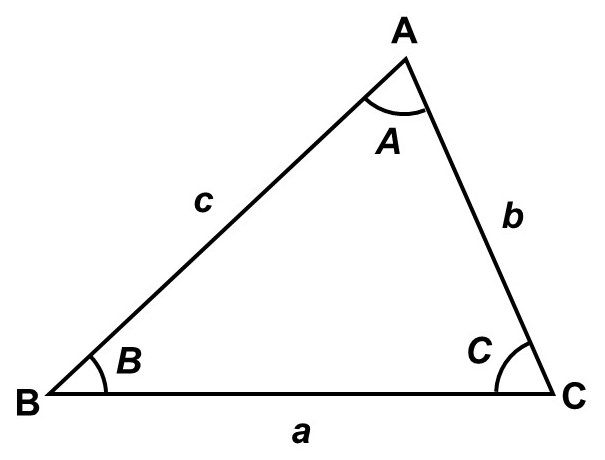
もっと要素をしぼることはできないでしょうか?そこで、次の$\triangle \mathrm{ABC}$と合同な$\triangle \mathrm{A’B’C’}$を作るのに必要な条件を考えてみましょう[1]。
1辺の長さが等しい場合
1辺の長さが等しい($\mathrm{B’C’} = a$)場合を考えてみます。
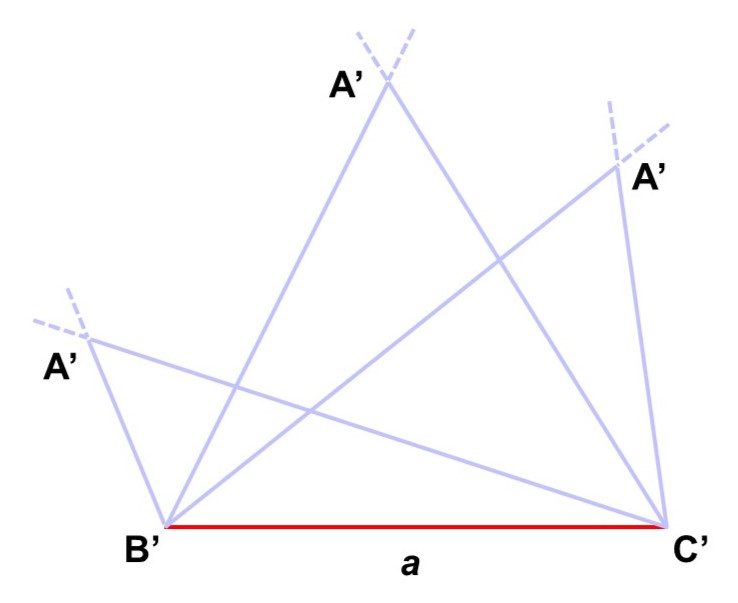
さすがにこの条件だけでは合同な三角形は作れません。というのも、内角についての情報がないため、頂点$\mathrm{A’}$の位置が決まらず、$\triangle \mathrm{A’B’C’}$の作り方が無数に出てきてしまうからです。
では、$\mathrm{B’C’}$の両端の内角が$\angle \mathrm{A’B’C} = B$, $\angle \mathrm{B’C’A’} = C$とわかっていたらどうでしょうか?これなら頂点$\mathrm{A’}$の位置は1通りに決まり、$\triangle \mathrm{A’B’C’}$は$\triangle \mathrm{ABC}$と合同な三角形になります。
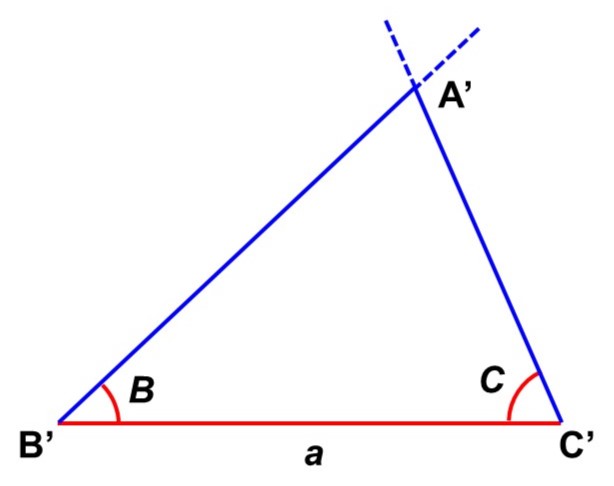
つまり、1辺とその両端の角がそれぞれ等しければ、合同な三角形を作ることができます。
2辺の長さが等しい場合
今度は2辺の長さが等しい($\mathrm{B’C’} = a$, $\mathrm{A’B’} = c$)場合を考えてみます。
先ほどよりは条件が強いものの、これでは合同な三角形は作れません。この場合、$\angle \mathrm{A’B’C’}$についての情報がないので、$\mathrm{C’A’}$の長さが決まらず、やはり$\triangle \mathrm{A’B’C’}$の作り方は無数に出てきてしまいます。
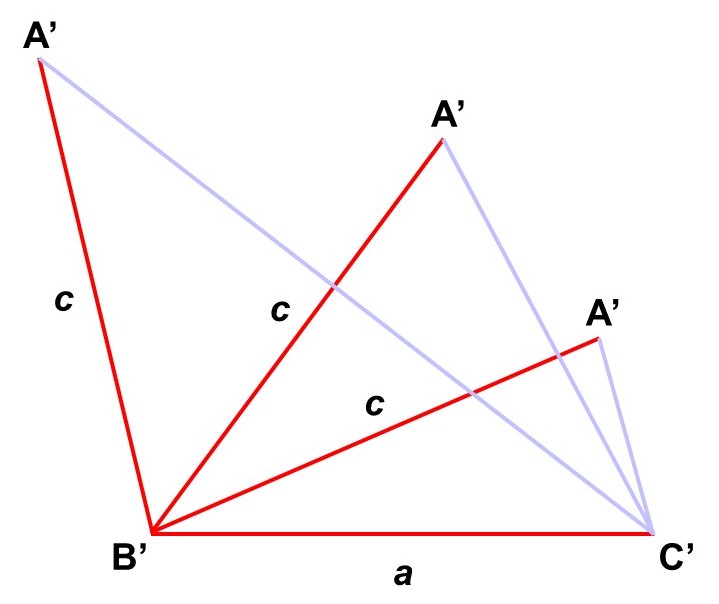
なので、$\angle \mathrm{A’B’C’} = B$とわかっている場合を考えましょう。これなら$\mathrm{C’A’}$の長さが決まり、$\triangle \mathrm{A’B’C’}$は$\triangle \mathrm{ABC}$と合同な三角形になります。
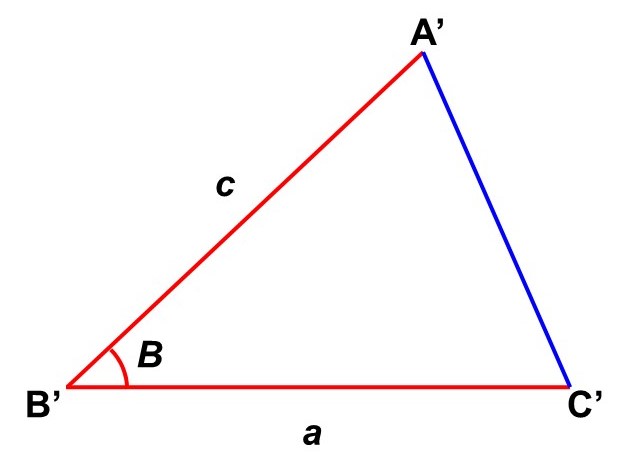
つまり、2辺とその間の角がそれぞれ等しければ、合同な三角形を作ることができます。
3辺の長さが等しい場合
続いて3辺の長さが等しい($\mathrm{B’C’} = a$, $\mathrm{C’A’} = b$, $\mathrm{A’B’} = c$)場合を考えてみます。
この場合はどの辺の長さも変わりようがなく、ゆえに内角が変わってしまうこともありません。すなわち、$\triangle \mathrm{A’B’C’}$の作り方は1通りしかなく、それは$\triangle \mathrm{ABC}$と合同な三角形ということになります。
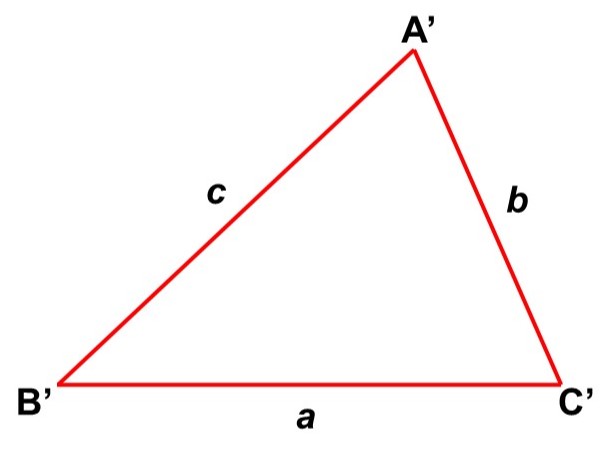
よって、3辺の長さがそれぞれ等しければ、合同な三角形を作ることができます。
以上から、合同な三角形を作るには次のいずれかのパターンで条件をみたせばよいということになります。いずれもチェックする要素は3つなので、辺と角の6つすべてを確認するよりもずっと楽ですね。
<2つの三角形が合同であるための条件>
- 1辺とその両端の角がそれぞれ等しい
- 2辺とその間の角がそれぞれ等しい
- 3辺がそれぞれ等しい
「合同」を使って図形を調べてみよう
ここまで見てきたように、ある図形に対して
- いくつかの三角形に分ける
- 条件を使ってそれぞれの三角形と合同な三角形を作る
- 作った三角形を組み合わせる
という手順を踏むことで、元の図形と同じ(合同な)図形が得られます。
ただ、「合同」という考え方にはもう一つの使い方があります。それは「図形の持つ性質を調べる」ことです。
ここでは二等辺三角形と平行四辺形を例に、「合同」を使ってこれらの図形にかくされた性質を解き明かしてみましょう。
二等辺三角形
30Fでも紹介しましたが、二等辺三角形とは「2辺の長さが等しい」三角形のことです。
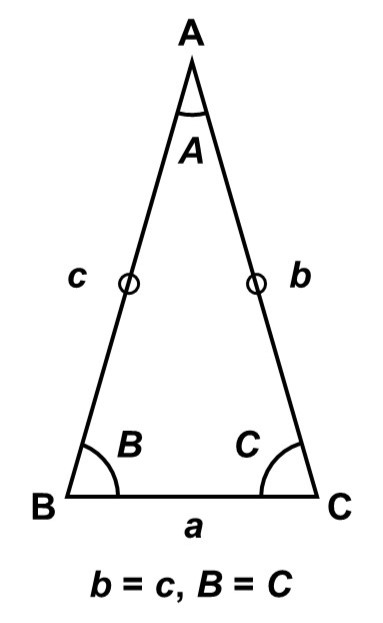
二等辺三角形には「底角が等しい($B = C$)」という性質がありますが、この理由を「合同」を使って確かめてみましょう。
命題:
$\triangle \mathrm{ABC}$が$\mathrm{AB} = \mathrm{AC}$の二等辺三角形であるならば、$B = C$が成り立つ。
証明:
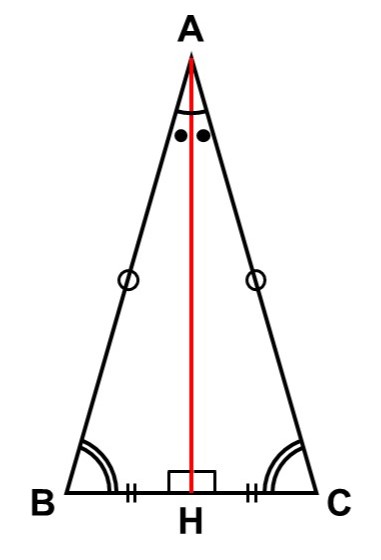
角$A$を二等分するように頂点$\mathrm{A}$から対辺$\mathrm{BC}$に向かって直線を引き、$\mathrm{BC}$との交点を$\mathrm{H}$とする。

この時、$\triangle \mathrm{ABH}$と$\triangle \mathrm{ACH}$について、次のことが言える。
- 辺$\mathrm{AH}$が共通している。 <1>
- $\mathrm{AH}$は角$A$の二等分線なので、
$\angle \mathrm{HAB} = \angle \mathrm{HAC}$ <2>
- $\triangle \mathrm{ABC}$は二等辺三角形であり、$\mathrm{AB} = \mathrm{AC}$ <3>
よって<1>, <2>, <3>から、$\triangle \mathrm{ABH}$と$\triangle \mathrm{ACH}$は「2辺とその間の角がそれぞれ等しい」ので合同である。
したがって、対応する角は等しく、
$\angle \mathrm{ABH} = \angle \mathrm{ACH}$
すなわち$B = C$が成り立つ。(証明終)
今回のように、時には補助線を引いて考えることもありますが、合同を使って図形を調べる時のポイントは
- わかっていることを使って2つの三角形の合同を示す
- 合同であることを使って、わからなかった辺や角が等しいことをつきとめる
の2つです。
ちなみに、2つの三角形が合同であることを簡単に表すために「≡」という記号がよく使われます。例えば今回の場合だと
$\triangle \mathrm{ABH} \equiv \triangle \mathrm{ACH}$
のような感じですね。ぜひ覚えておきましょう。
平行四辺形
平行四辺形とは、その名の通り「平行な2組の線分によって作られる四角形」のことです。
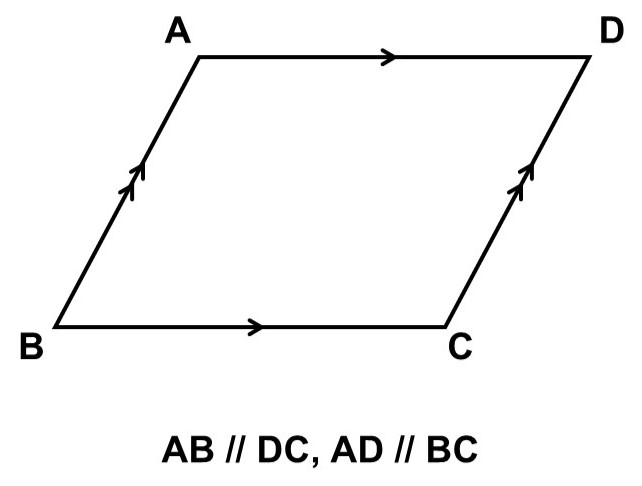
この四角形には、次のような性質があることが知られています。
- 2組の対辺はそれぞれ等しい
- 2組の対角はそれぞれ等しい
- 2本の対角線の交点$\mathrm{M}$は対角線をそれぞれ二等分する
※点$\mathrm{M}$のように線分を二等分する点を中点といいます。
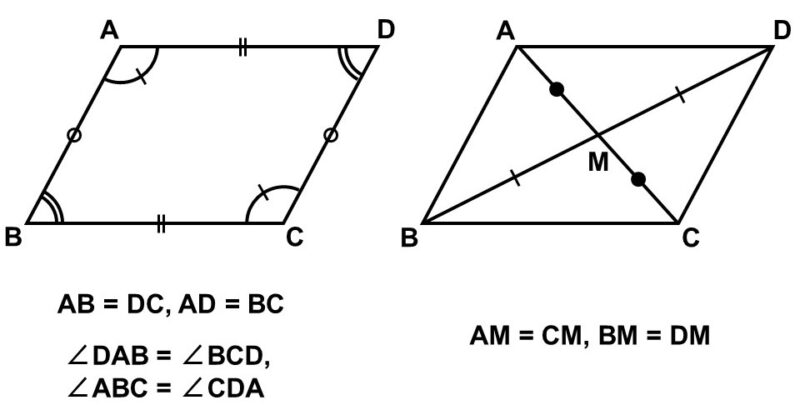
この3つの性質を「合同」を使って確かめてみましょう。最初の2つは同時に確認できるので、まずこちらを証明します。
命題1:
四角形$\mathrm{ABCD}$が平行四辺形ならば、次が成り立つ。
- $\mathrm{AB} = \mathrm{DC}$, $\mathrm{AD} = \mathrm{BC}$
- $\angle \mathrm{DAB} = \angle \mathrm{BCD}$,
$\angle \mathrm{ABC} = \angle \mathrm{CDA}$
証明:
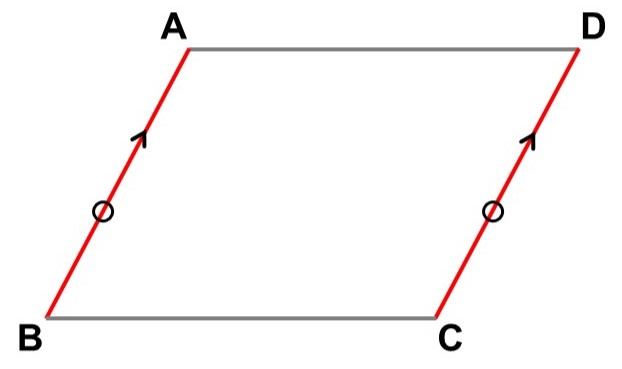
平行四辺形$\mathrm{ABCD}$に対して対角線$\mathrm{BD}$を引く。
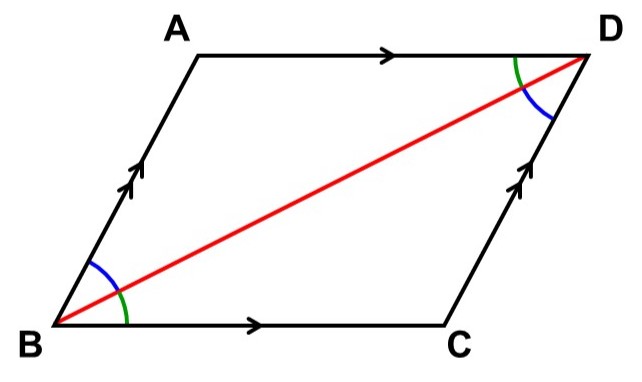
この時、$\triangle \mathrm{ABD}$と$\triangle \mathrm{CDB}$について、次のことが言える。
- 辺$\mathrm{BD}$が共通している。 <1>
- $\mathrm{AB} /\!/ \mathrm{DC}$より、錯角が等しいので、
$\angle \mathrm{ABD} = \angle \mathrm{CDB}$ <2>
- $\mathrm{AD} /\!/ \mathrm{BC}$より、錯角が等しいので、
$\angle \mathrm{BDA} = \angle \mathrm{DBC}$ <3>
よって<1>, <2>, <3>から、$\triangle \mathrm{ABD}$と$\triangle \mathrm{CDB}$は「1辺とその両端の角がそれぞれ等しい」ので合同である。
したがって、対応する辺は等しく、
$\mathrm{AB} = \mathrm{CD}$, $\mathrm{DA} = \mathrm{BC}$
また、対応する角も等しく、
$\angle \mathrm{DAB} = \angle \mathrm{BCD}$
さらに<2>, <3>から、
$\begin{align}
&\hspace{30pt} \angle \mathrm{ABD}+\angle \mathrm{DBC} = \angle \mathrm{CDB}+\angle \mathrm{BDA} \\[1.5ex]
&\iff \hspace{3pt} \angle \mathrm{ABC} = \angle \mathrm{CDA}
\end{align}$
となる。(証明終)
続いて、3つ目の性質の証明です。こちらの証明には、今示した性質の1つ「2組の対辺がそれぞれ等しい」をさっそく使っていきます。
命題2:
四角形$\mathrm{ABCD}$が平行四辺形ならば、2本の対角線の交点$\mathrm{M}$に対して、
$\mathrm{AM} = \mathrm{CM}$, $\mathrm{BM} = \mathrm{DM}$
が成り立つ。
証明:
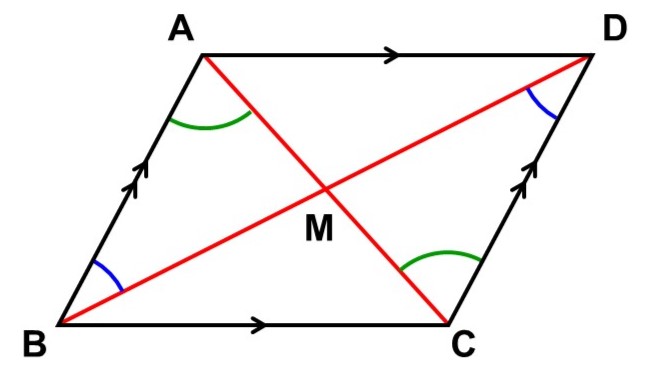
$\triangle \mathrm{ABM}$と$\triangle \mathrm{CDM}$について、次のことが言える。
- 平行四辺形$\mathrm{ABCD}$においては対辺が等しいので、
$\mathrm{AB} = \mathrm{CD}$ <1>
- $\mathrm{AB} /\!/ \mathrm{DC}$より、錯角が等しいので、
$\angle \mathrm{ABM} = \angle \mathrm{CDM}$ <2>
$\angle \mathrm{MAB} = \angle \mathrm{MCD}$ <3>
よって<1>, <2>, <3>から、$\triangle \mathrm{ABM}$と$\triangle \mathrm{CDM}$は「1辺と両端の角がそれぞれ等しい」ので合同である。
したがって、対応する辺は等しく、
$\mathrm{AM} = \mathrm{CM}$, $\mathrm{BM} = \mathrm{DM}$
が成り立つ。(証明終)
まとめ
今回は三角形の合同について学びました。合同条件を改めてまとめておきます。
- 1辺とその両端の角がそれぞれ等しい
- 2辺とその間の角がそれぞれ等しい
- 3辺がそれぞれ等しい
「合同」の考え方が理解できるようになると、同じ図形かどうかを確かめたり作ったりすることができるだけでなく、それまでかくれていた図形の性質が見えてきます。
うまく活用して図形の理解に役立てていきましょう。
今回はここまでです。お疲れさまでした!
参考資料
暗記しなければならないというイメージの強い「三角形の合同条件」ですが、今回紹介した「より少ない要素で合同な三角形を作る」という考え方は、そのイメージをやわらげてくれるはずです。
以下の書籍に同様の考え方が載っていますので、ぜひ参考にしてみてください。
[1] カジュアルな算数・数学の話 (鶴崎修功 / クラーケンラボ 2021)