こんにちは、まてがめです。
前回は、平面図形における大切な考え方の1つ「合同」、そして合同な図形を作ったり図形を調べたりするのに必要な「三角形の合同条件」について学びました。
前回に引き続き、今回も三角形について掘り下げていきます。今回のテーマは「小さな三角形を使って、直接は測れない長さを求める方法」です。
この章の初めにも話したように、もともと幾何学という学問は、土地の区画や大きな建物の建造、天体観測のように「物を測りたい」というモチベーションから発展してきました。
こうしたモチベーションから生まれたのが、今回学ぶ相似（そうじ）と三角比です。これを使うと、自分の体よりもずっと大きなもの、例えばピラミッドの高さなんかもわかってしまいます。
この階で間違いなくあなたの見える景色は大きく変わるはずです！
相似とは？
復習ですが、前回解説した「合同」とは、「形も大きさも全く同じで、重ね合わせるとぴったり一致する図形」のことでした。一方、相似（そうじ）はこの条件を少しゆるくした考え方で「形のみが同じ図形」のことをいいます。
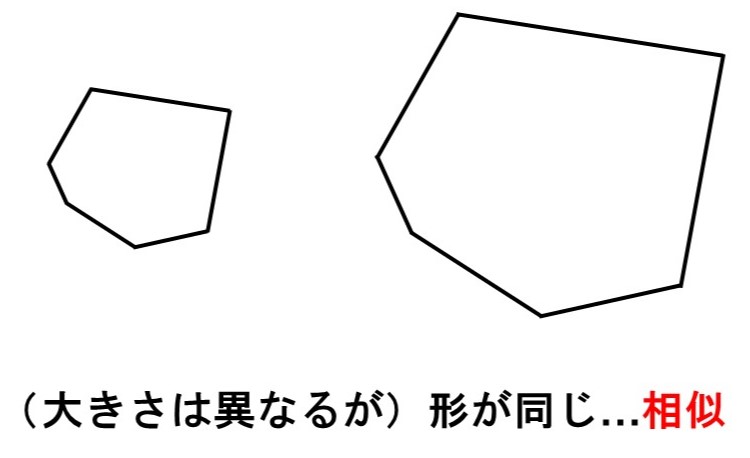
つまり大きさは関係ないので、ある図形を拡大・縮小した図形は元の図形と相似の関係にあると言えます。「プリンター」のイメージと言えばわかりやすいでしょうか？
したがって、2つの図形（多角形）が相似の関係にある時は、次のような性質があります。
- 対応する線分の長さの比率は常に等しい
- 対応する角度は等しい
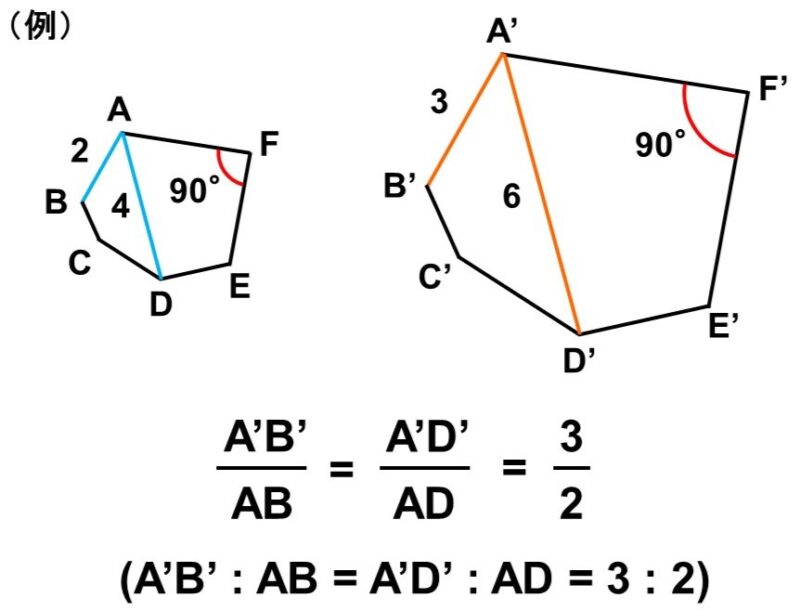
この2つは相似の考え方の基礎になるので、よく覚えておいてください。
三角形の相似条件
あらゆる平面図形は三角形に分けることができるので、図形の相似を理解するには、まず三角形の相似について理解することが大切です。そこで、2つの三角形が相似となるための条件を考えてみましょう。
といってもこれは意外と簡単で、前回学んだ三角形の合同条件において、大きさ（辺の長さ）にかかわる条件を少しゆるくしてあげるだけです。
2つの角がそれぞれ等しい
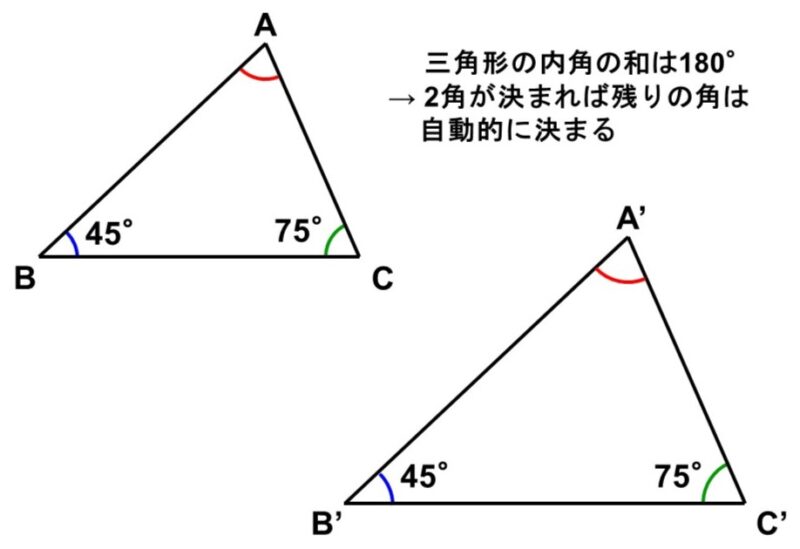
これは、三角形の合同条件の1つ「1辺とその両端の角がそれぞれ等しい」をゆるくしたものです。
三角形の内角の和は必ず180°になりますから、結局2つの角がそれぞれ等しければ、自動的に残り1つの角も互いに等しくなり、三角形の形は同じ、すなわち相似になります。
2つの角だけで相似かどうかがわかるため、とても使い勝手のよい条件です。
2辺の長さの比とその間の角がそれぞれ等しい
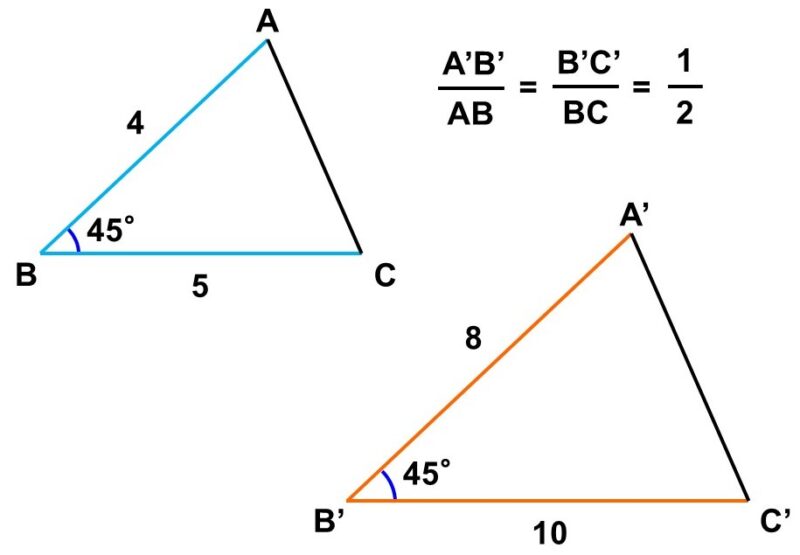
これは、三角形の合同条件の1つ「2辺とその間の角がそれぞれ等しい」をゆるくしたものです。
相似において辺の長さ自体は問題にならず、辺の長さの比率さえあっていればよいので、このような条件になります。この考え方が測量への応用につながっていきます。
3辺の長さの比がそれぞれ等しい
これは三角形の合同条件の1つ「3辺の長さがそれぞれ等しい」をゆるくしたもので、こちらも辺の長さの比率さえあっていれば形は同じになるという考え方です。
「相似」を使うといろんな長さがわかる
「相似」の考え方がわかるようになると、比率を使って未知の長さを調べることができます。簡単な例を2つほどを紹介します。
（例1）
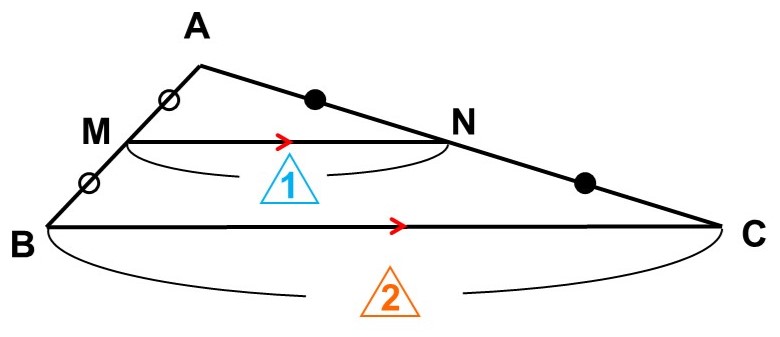
$\triangle \mathrm{ABC}$があり、$\mathrm{AB} = 2$, $\mathrm{BC} = 6$, $\mathrm{AC} = 5$である。また、辺$\mathrm{AB}$, $\mathrm{AC}$の中点をそれぞれ$\mathrm{M}$, $\mathrm{N}$とする。
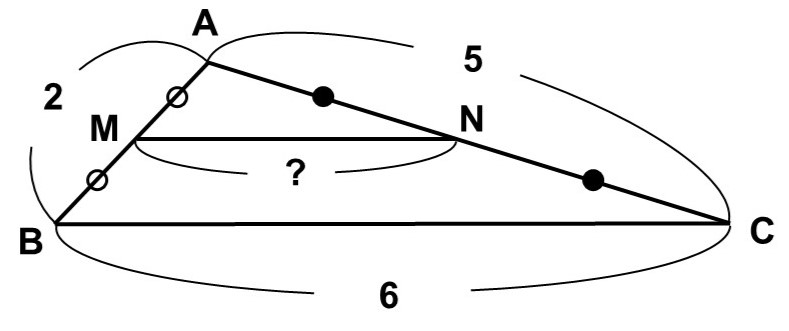
この図形において、線分$\mathrm{MN}$の長さを求めてみよう。
$\triangle \mathrm{ABC}$と$\triangle \mathrm{AMN}$について次のことが言える。
- $\angle \mathrm{CAB} = \angle \mathrm{NAM}$ <1>
- $点\mathrm{M}$は$\mathrm{AB}$の中点なので、
$\mathrm{AB} : \mathrm{AM} = 2 : 1$ <2>
- $点\mathrm{N}$は$\mathrm{AC}$の中点なので、
$\mathrm{AC} : \mathrm{AN} = 2 : 1$ <3>
よって<1>, <2>, <3>から、$\triangle \mathrm{ABC}$と$\triangle \mathrm{AMN}$は、2辺の長さの比とその間の角がそれぞれ等しいので相似である。
つまり、対応する辺の比も等しく、
$\mathrm{BC} : \mathrm{MN} = 2 : 1$
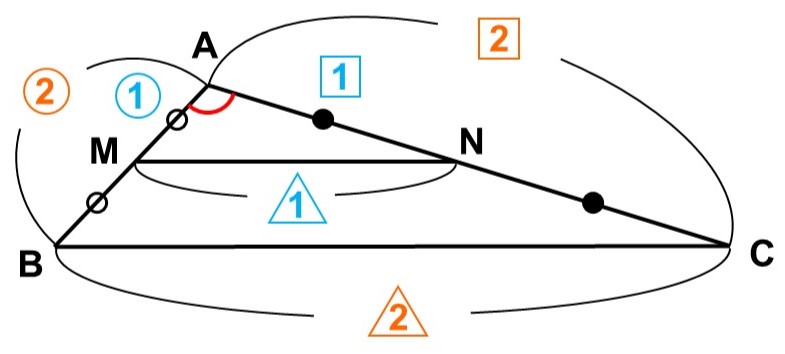
したがって、$\mathrm{MN}$の長さは
$\mathrm{MN} = \mathrm{BC} \times \dfrac{1}{2} = 3$
この例では$\triangle \mathrm{ABC}$と$\triangle \mathrm{AMN}$が相似であることを示しましたが、2つの図形が相似であることを簡潔に示す時には「∽」という記号がよく使われます。今回の例であれば、
$\triangle \mathrm{ABC}$ ∽ $\triangle \mathrm{AMN}$
といった感じですね。
例1のように、$\triangle \mathrm{ABC}$の2辺$\mathrm{AB}$, $\mathrm{AC}$に中点$\mathrm{M}$, $\mathrm{N}$をとると、$\triangle \mathrm{ABC}$ ∽ $\triangle \mathrm{ABC}$となるため、次が成り立ちます。
$\mathrm{MN} = \dfrac{\mathrm{BC}}{2}$
$\mathrm{MN} // \mathrm{BC}$
相似を使えばすぐにわかることではありますが、この性質は特別に中点連結定理（ちゅうてんれんけつていり）という名前で呼ばれています。
（例2）
長方形$\mathrm{ABCD}$があり、$\mathrm{AD} = \mathrm{BC} = 6$である。
辺$\mathrm{AD}$の中点を$\mathrm{M}$、辺$\mathrm{BC}$を1 : 2に内分する点を$\mathrm{N}$とし、対角線$\mathrm{AC}$と線分$\mathrm{MN}$の交点を$\mathrm{P}$とする。
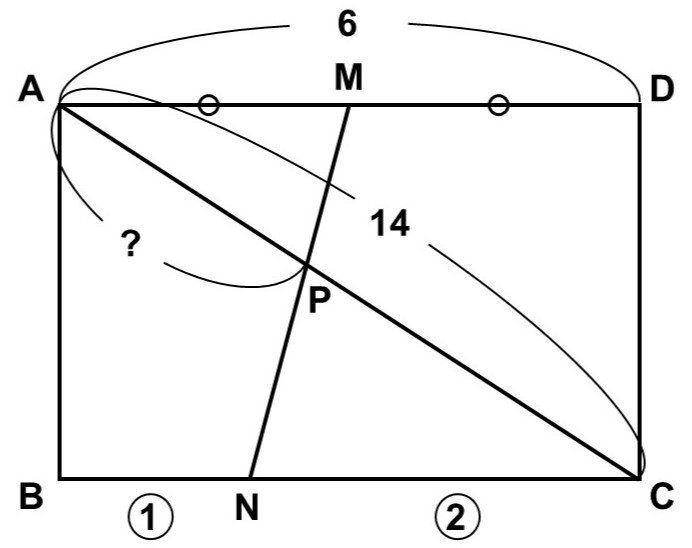
$\mathrm{AC} = 14$の時、線分$\mathrm{AP}$の長さを求めてみよう。
まず、条件から次のことがわかっている。
$\mathrm{AM} : \mathrm{MD} = 1 : 1$ <1>
$\mathrm{BN} : \mathrm{NC} = 1 : 2$ <2>
よって<1>から、
$\mathrm{AM} = \mathrm{AD} \times \dfrac{1}{2} = 3$
<2>から、
$\mathrm{NC} = \mathrm{BC} \times \dfrac{2}{1+2} = 4$
とわかる。
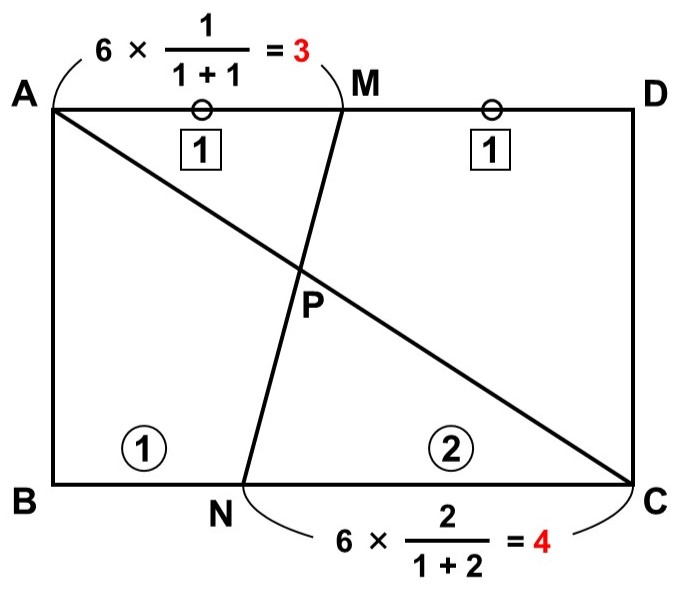
また、$\triangle \mathrm{APM}$と$\triangle \mathrm{CPN}$については次のことが言える。
- 四角形$\mathrm{ABCD}$は長方形であり、$\mathrm{AD} /\!/ \mathrm{BC}$なので、錯角が等しく、
$\angle \mathrm{MAP} = \angle \mathrm{NCP}$ <3>
$\angle \mathrm{PMA} = \angle \mathrm{PNC}$ <4>
よって<1>, <2>から、$\triangle \mathrm{APM}$と$\triangle \mathrm{CPN}$は2つの角がそれぞれ等しいので相似である。
したがって、対応する辺の比は等しく、
$\mathrm{AP} : \mathrm{CP} = \mathrm{AM} : \mathrm{CN} = 3 : 4$
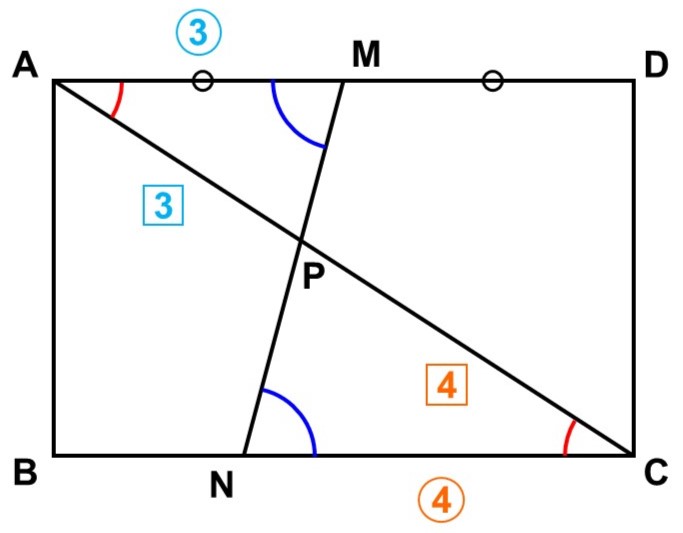
これより、線分$\mathrm{AP}$の長さは
$\mathrm{AP} = \mathrm{AC} \times \dfrac{3}{3+4} = 6$
相似を測量へ応用する ― タレスの例
相似が便利な理由は「形が同じなら辺の長さの比率が変わらない」という点にあります。古代の人々はこのことを直接測ることが難しいものに利用することを思いつきました。
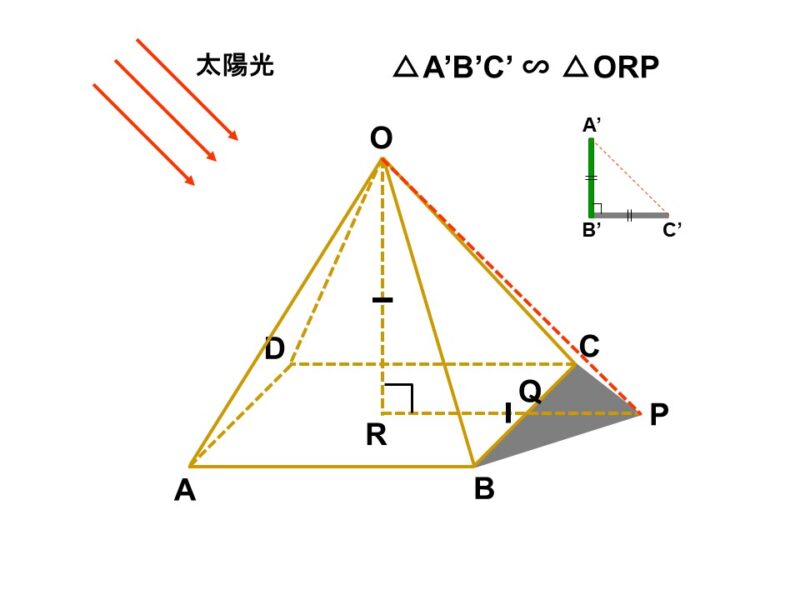
例えば古代ギリシャ人の哲学者タレスは、自分よりもずっと大きいピラミッドの高さを次のようにして測量したとされています[1]。
（前提）
- ピラミッドは底面が正方形である、次のような立体$\mathrm{OABCD}$（四角すいといいます）とする。
- 底面の正方形の1辺の長さ（例えば辺$\mathrm{AB}$）については直接測ることができるものとする。
（方法）
<1> ピラミッドの近くに小さな棒を垂直に立て、棒の長さ（$\mathrm{A’B’}$）と太陽光によってできる影の長さ（$\mathrm{B’C’}$）が等しくなるタイミングを待ちます。この時、$\triangle \mathrm{A’B’C’}$は直角二等辺三角形になります。
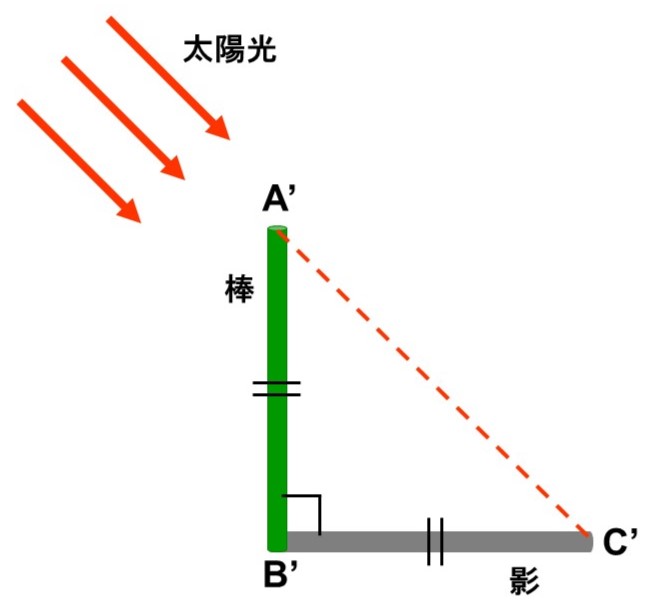
<2> 棒の長さと影の長さが等しくなったら、ピラミッドによってできる影の長さ（$\mathrm{PQ}$）を測ります。
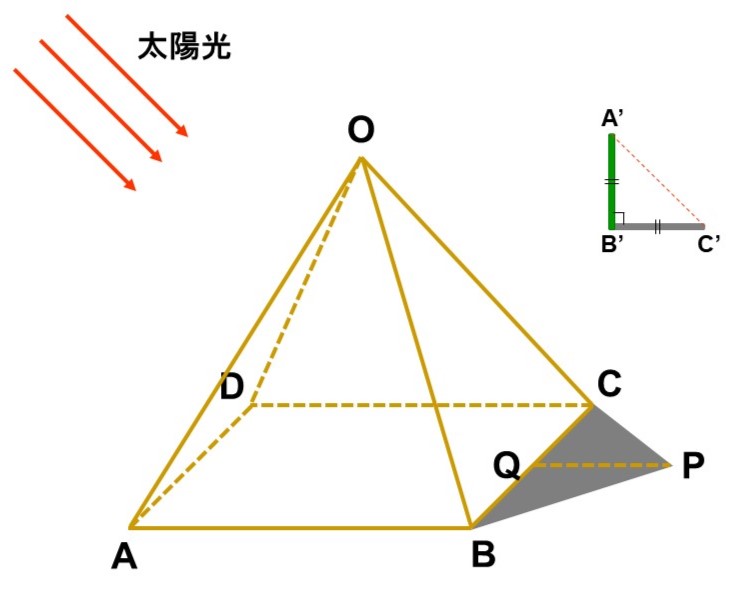
<3> 今求めたいピラミッドの高さとは、底面の正方形$\mathrm{ABCD}$から頂点$\mathrm{O}$までの距離のことです。
これは次の図の線分$\mathrm{OR}$の長さにあたるわけですが、棒の頂点とピラミッドの頂点に向かってくる太陽光は同じ角度で入射しているので、$\triangle \mathrm{ABC}$ ∽ $\triangle \mathrm{ORP}$が成り立ちます。つまり、$\triangle \mathrm{ORP}$もまた直角二等辺三角形ということです。
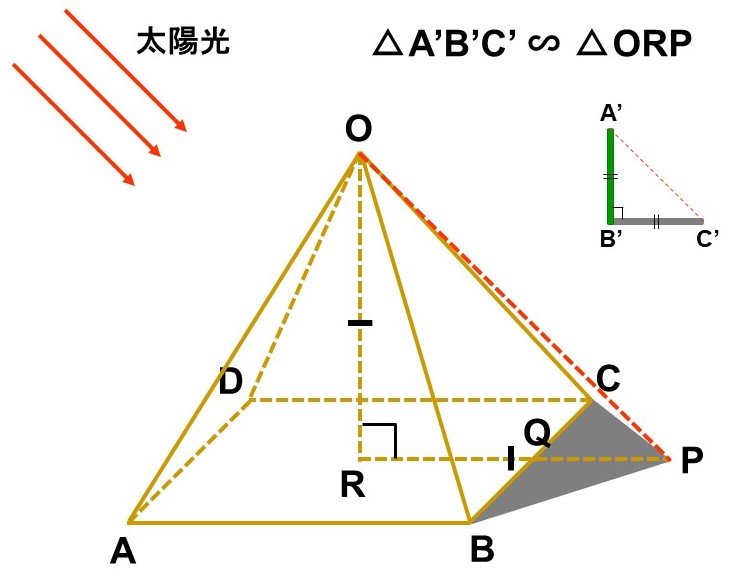
よって$\mathrm{OR} = \mathrm{RP}$なので、$\mathrm{RP}$の長さを考えてみます。
$\begin{align}
\mathrm{RP} &= \mathrm{PQ}+\mathrm{QR} \\[1.5ex]
&= \mathrm{PQ}+\dfrac{\mathrm{AB}}{2}
\end{align}$
と表せるので、ピラミッドの影の長さ（$\mathrm{PQ}$）とピラミッド底面の1辺の長さ（$\mathrm{AB}$）からピラミッドの高さが求まります。
相似の力、少しは感じていただけたでしょうか？
相似をもっと使いやすく ― 三角比
タレスは相似な2つの直角二等辺三角形に注目してピラミッドの高さを求めてみせました。ポイントは「基準となる直角三角形を用意している」という点です。
これはすなわち、「何かの長さを測りたいと思った時は、相似な直角三角形を用意すれば測量できる」ということを意味しています。
ただ、測量のたびに直角三角形を用意するのはめんどうです。そこで、古代の人はこう考えました。
「直角三角形における角度と辺の比率の関係をあらかじめ表にまとめておけばよいのでは？」
こうして生まれたのが三角比と呼ばれるものです。もっとも有名なのがcos（コサイン、余弦）, sin（サイン、正弦）, tan（タンジェント、正接）で、わかっている角度や辺の長さの情報に応じて使い分けます[1], [2]。
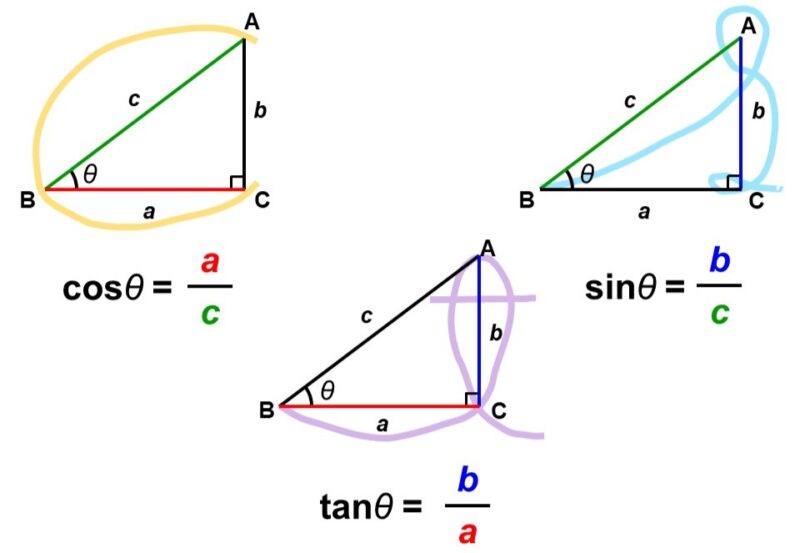
cos（コサイン、余弦）
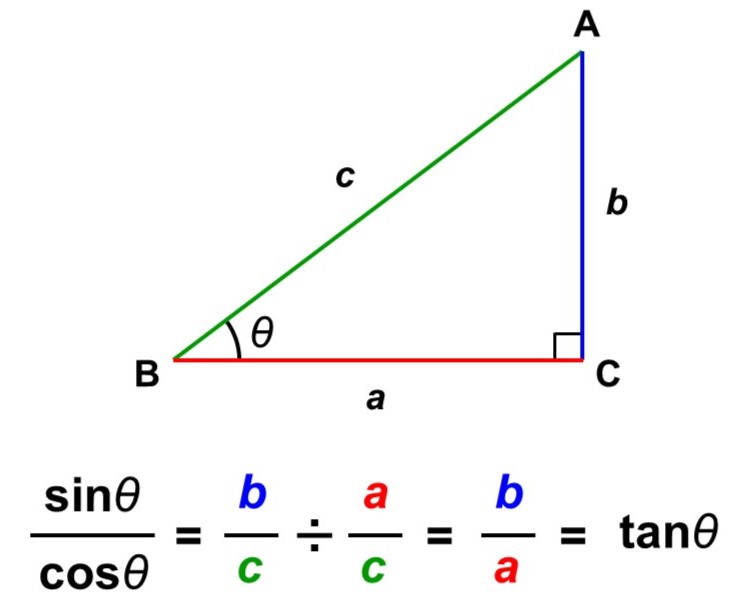
$\cos$（コサイン、余弦）は、角度$\theta$の直角三角形に対して、次のような辺の比率を考えるものです。
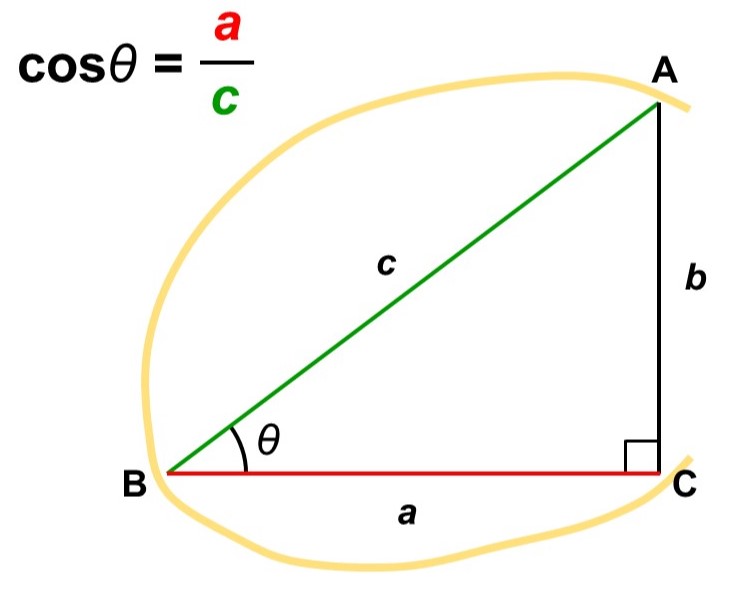
角度$\theta$が間にくるように辺の比をとります。$\cos$の”c“をイメージすると覚えやすいです。
そして角度$\theta$と$\cos \theta$の対応を、例えば5°ずつ調べていくと、次の表のようになります※。
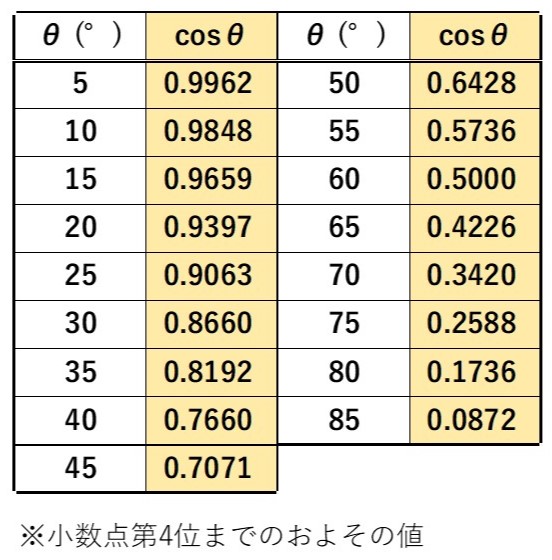
このように角度と辺の比率の関係がわかっていれば、例えば次のように角度や長さをすぐに計算で求めることができます（≒は「ほぼ等しい」という意味）。
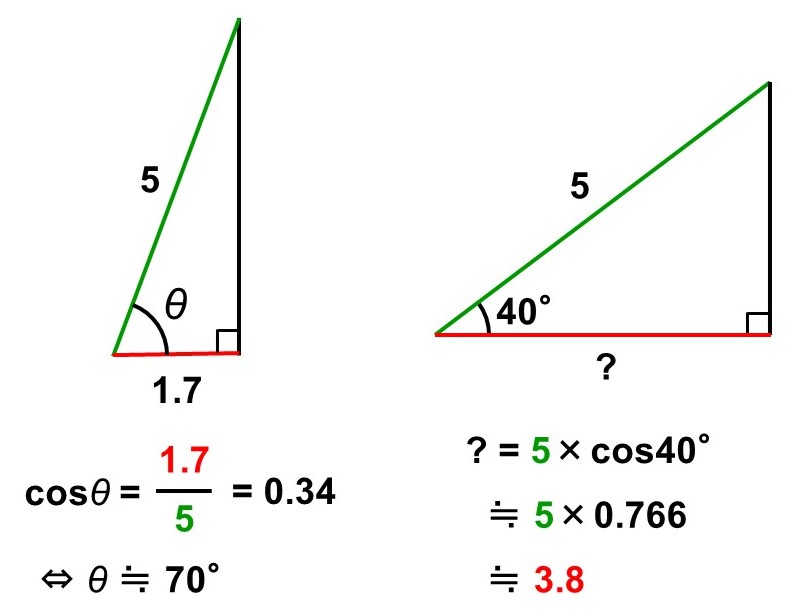
相似な直角三角形を改めて用意しなくても相似を利用できるのが、三角比の強みです。
sin（サイン、正弦）
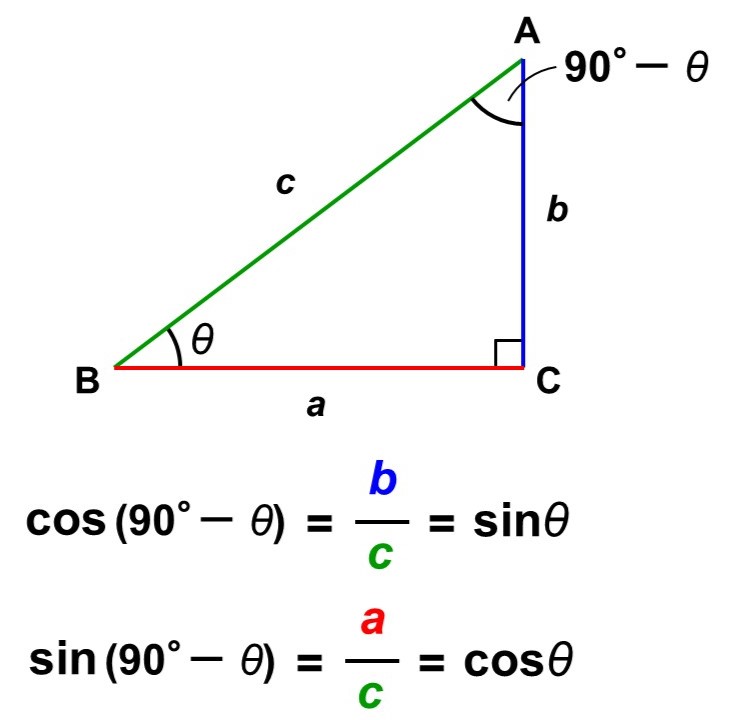
$\sin$（サイン、正弦）は、角度$\theta$の直角三角形に対して、次のような辺の比率を考えるものです。
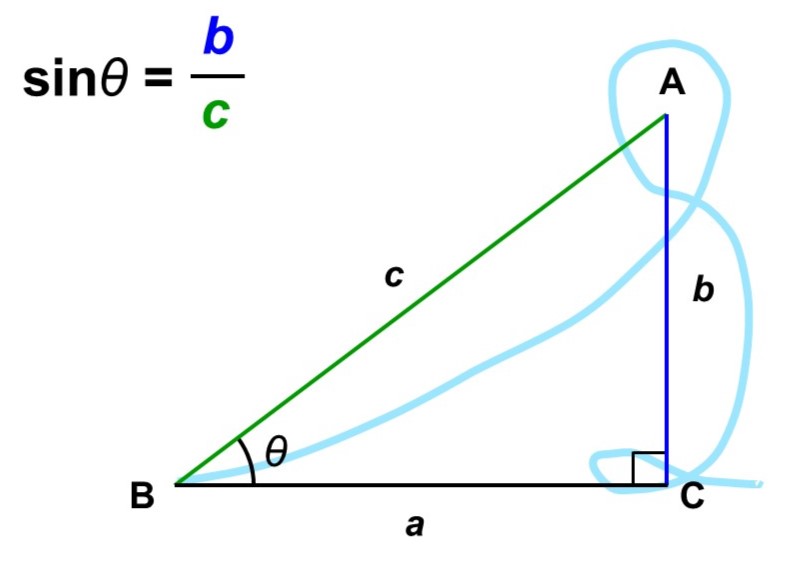
こちらは角度$\theta$ではないもう一方の鋭角（余角）が間にくるように辺の比をとります。$\sin$の”s“（の筆記体）をイメージすると覚えやすいです。
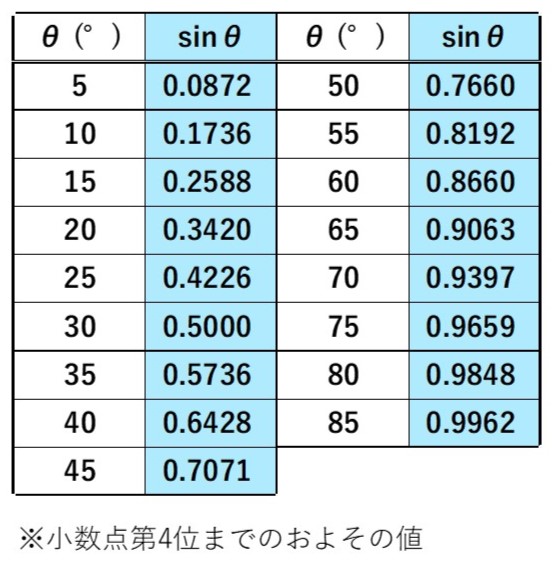
角度$\theta$と$\sin \theta$の対応は次の表のようになります※。
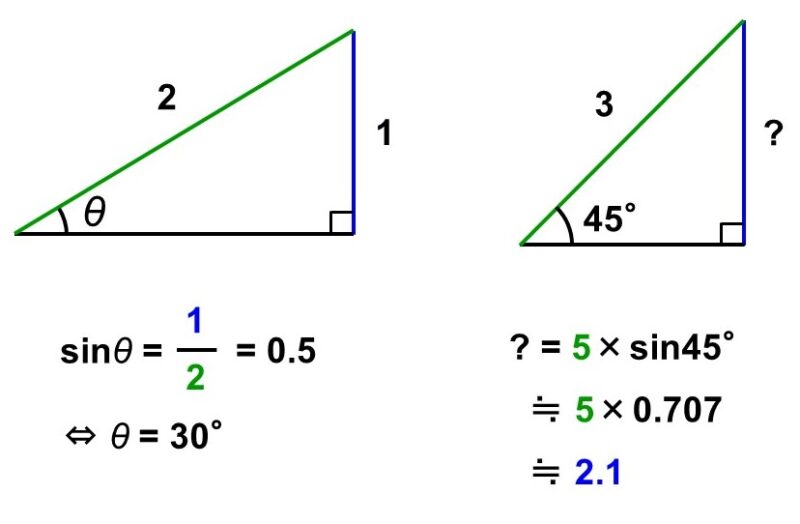
$\cos$と同じく、これを使うと次のように角度や長さを計算できます。
tan（タンジェント、正接）
$\tan$（タンジェント、正接）は、角度$\theta$の直角三角形に対して、次のような辺の比率を考えるものです。
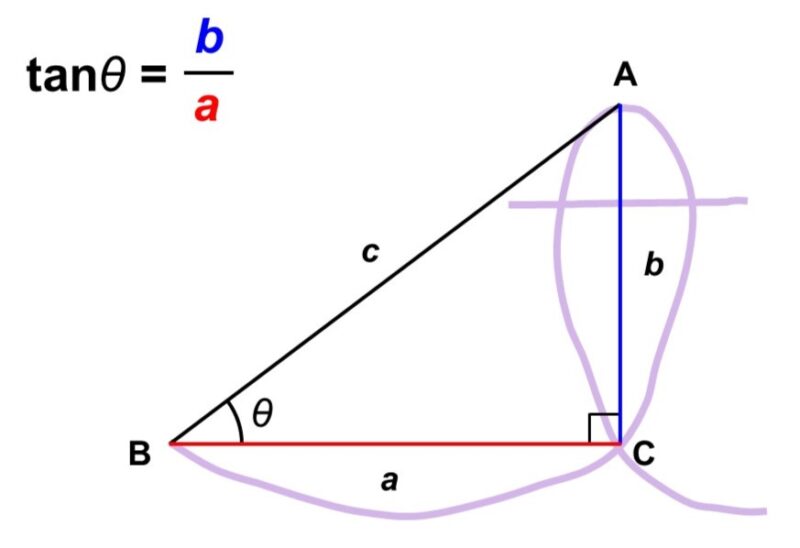
こちらは直角が間にくるように辺の比をとります。$\tan$の”t“（の筆記体）をイメージすると覚えやすいです。
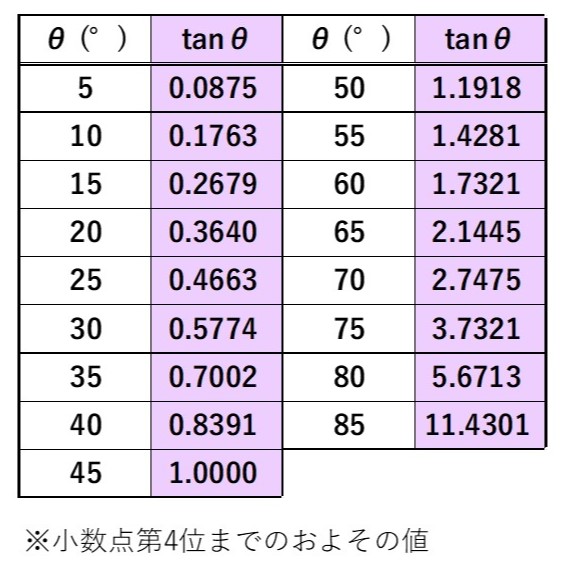
角度$\theta$と$\tan \theta$の対応は次の表のようになります※。
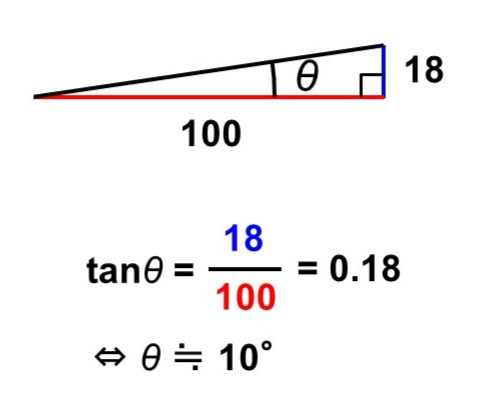
$\tan$は$\cos$, $\sin$同様に長さの計算にも使えますが、角度を求めたり傾きの程度を表したりするために使われることも多いです。
三角比の定義から、三角比同士にはいくつかの関係式が成り立ちます。いずれもよく使うものなので、直角三角形における意味と合わせて覚えておきましょう。
- $\tan \theta = \dfrac{\sin \theta}{\cos \theta}$
- $\cos(90^{\circ}-\theta) = \sin \theta$, $\sin(90^{\circ}-\theta) = \cos \theta$
まとめ
今回は相似と三角比について学びました。まとめると次のようになります。
- 相似：形が同じ図形。相似な図形はもう一方を拡大・縮小したものだと言える。
- 三角形の相似条件
- 2つの角がそれぞれ等しい
- 2辺の比とその間の角がそれぞれ等しい
- 3辺の比がそれぞれ等しい
- 相似を使うことで直接測れない長さの測量ができる。
- 三角比（cos, sin, tan）を使うと相似がより扱いやすくなる。
「相似」の考え方は「合同」と同じく、図形を理解するには欠かせないものです。まずは「相似な三角形を見つける」ところから練習して、少しずつ扱えるようにしていくのがよいでしょう。
また、三角比は図形における長さ・角度を求めるための強力なツールです。この先の階でも使っていくので、使い慣れるまでの間はこの階でくり返し復習してみてください。
今回はここまでです。お疲れさまでした！
参考資料
[1] Newton別冊 知識ゼロでもよくわかる 三角関数の学びなおしにも最適 三角関数 改訂第3版 (礒田正美, 市川温子, 梶原浩一, 佐藤健一, 竹内淳, 平松正顕, 前田京剛, math channel（沼倫加, 横山明日希, 吉田真也）, 水谷仁, 三谷政昭, 山岸順一, 和田純夫 / ニュートンプレス 2022)
[2] ビジュアルガイド もっと知りたい数学 深遠なる「幾何学」の世界 (マイク・ゴールドスミス（訳：緑慎也） / 創元社 2021)
