こんにちは、まてがめです。
前回は「相似」の考え方と、それを発展させた「三角比」について学びました。
合同（形も大きさも同じ図形）の考え方からスタートして、「形」のみに注目したのが相似の考え方だと言えます。なので今度は「大きさ」に注目してみましょう。
そもそも、図形の「大きさ」はどのように表せばよいのでしょうか？相似の関係にある（＝形が同じ）図形同士なら一目で大小がわかりますが、形が異なる場合は辺や角度だけ見ても、その大小を比べることはできません。
この悩みを解決してくれるのが、今回学ぶ面積（めんせき）というものです。
「面積」があるからこそ、例えば土地の大きさを測って、その土地の価値を決めたり、収穫できる穀物の量を見積もったりすることもできるわけです（日本史でも太閤検地という言葉が出てきますよね）。
一番のつまづきポイント「なぜその計算で面積が求まるのか？」についても、この階でくわしく解説していきます！
面積とは？
面積とは、図形の大きさを表す指標です。1辺の長さが1の正方形を面積の単位（面積1）と定め、その何個分になるかで面積の大きさを決めます。
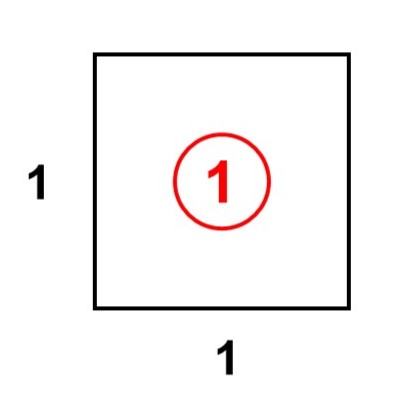
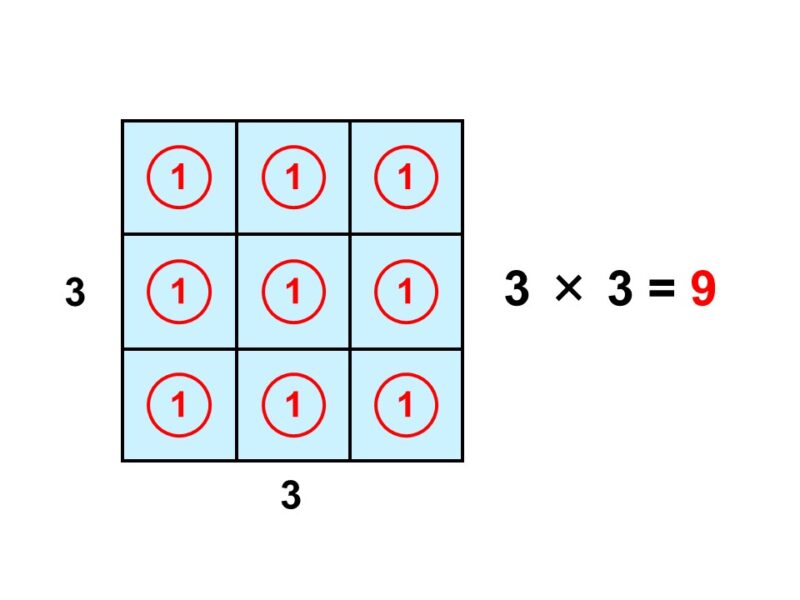
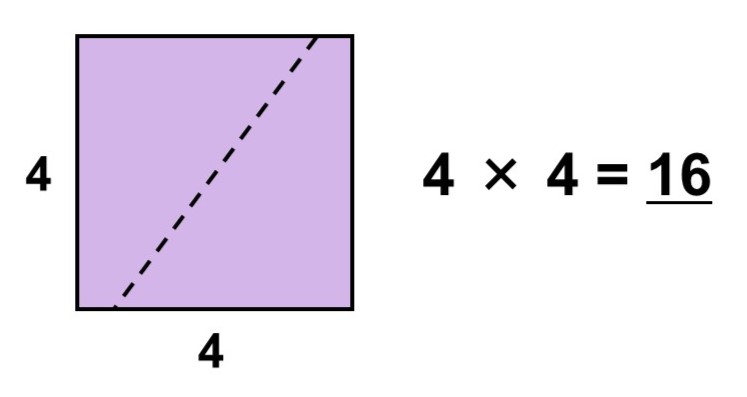
例えば、次の正方形の面積を計算してみましょう。
この正方形を面積1の正方形に細かく区切ると、次のようになります。
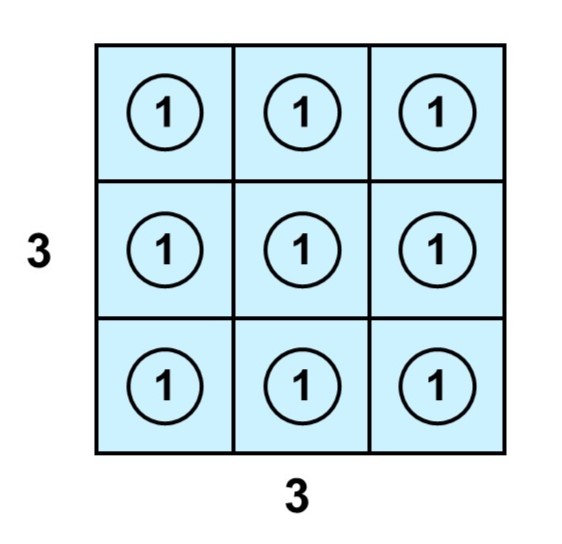
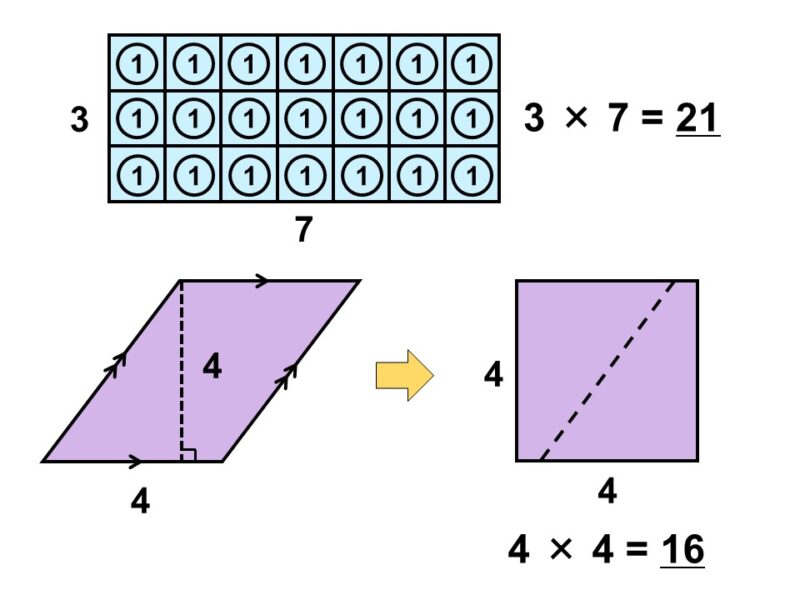
では、何個の正方形ができたか数えてみましょう。横に3個あって、それが3列あるので、掛け算の考え方で求まりますね。
$3 \times 3 = 9$
ですから、この正方形の面積は9ということがわかります。
このように面積は、「面積1の正方形が何個あるのか？」という考え方で計算します。これはどんな形の図形でも同じです。
辺の長さが分数や小数となる正方形についても、掛け算で計算できます。
例として、1辺の長さが2.5の正方形の面積を考えてみましょう。
これを正方形に分けてみると、1辺が1の正方形（4個）と1辺が$0.5 = \frac{1}{2}$の正方形（9個）が作れます。
1辺が1の正方形の面積はもちろん1です。対して、1辺が0.5（$= \frac{1}{2}$）の正方形の面積は、図からわかるように、ちょうど$\frac{1}{4}$になります。
したがって1辺が2.5の正方形は、面積1の正方形4個分と面積$\frac{1}{4}$の正方形9個分から成るので、求める面積は
$\begin{align}
& \hspace{13pt} 1 \times 4+\dfrac{1}{4} \times 9 \\[1.5ex]
&= 4+\dfrac{9}{4} \\[1.5ex]
&= \dfrac{25}{4} = 6.25
\end{align}$
となります。
では、1辺の長さから直接面積を計算してみるとどうなるでしょうか？
$2.5 \times 2.5 = 6.25$
確かに同じ答えになりました。このように、辺の長さが自然数でない場合でも、面積は掛け算で求めることができます。
正方形と同じ考え方で、長方形の面積も計算できます。
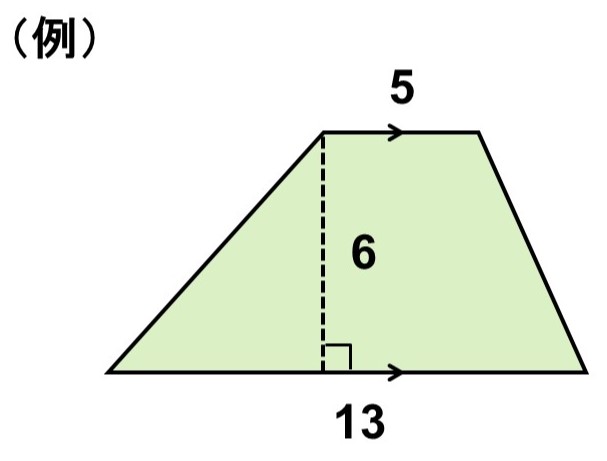
（例）
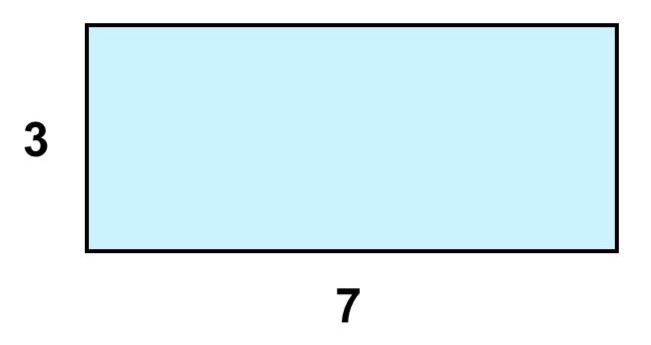
底辺が7、高さが3なので、面積1の正方形に分けると次のようになる。
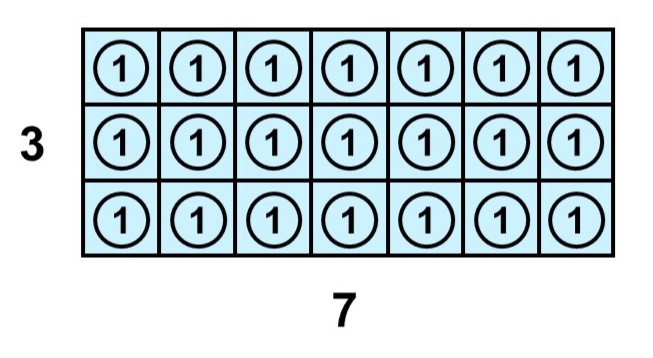
よって、求める面積は
$7 \times 3 = 21$
面積の基本がわかったところで、他の図形の面積の求め方についても考えていきます。
平行四辺形の面積
正方形・長方形の仲間である平行四辺形の面積はどう計算すればよいでしょうか？
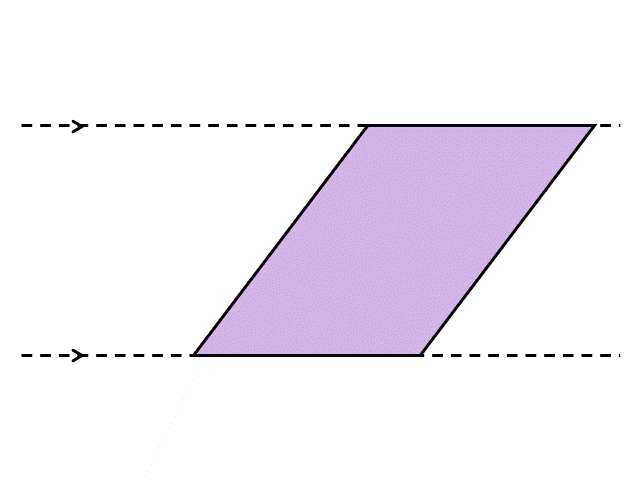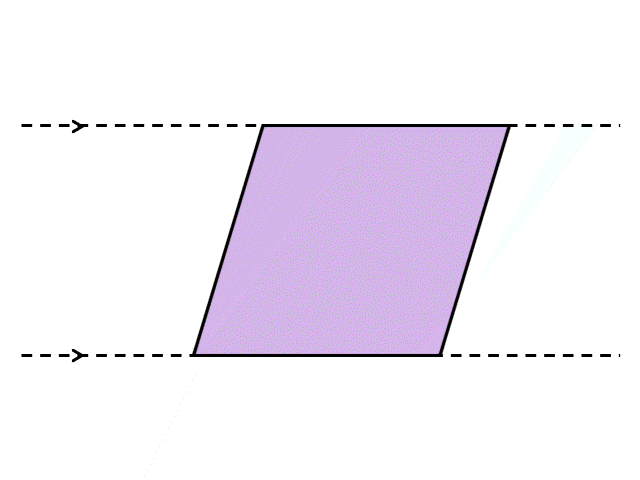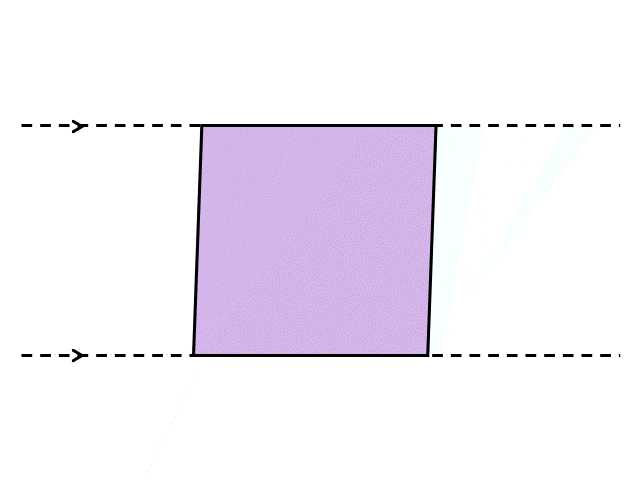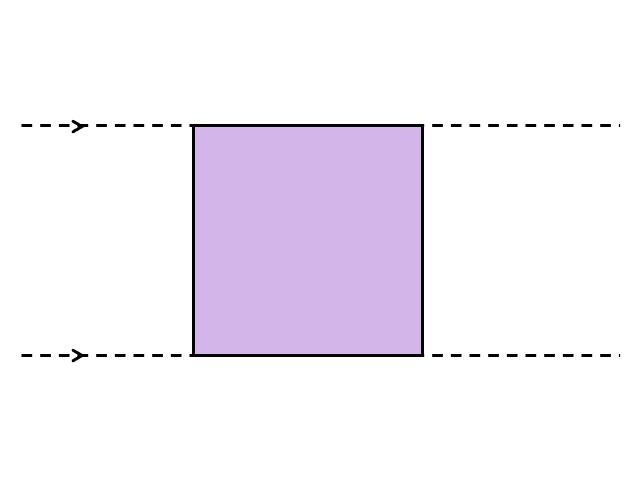
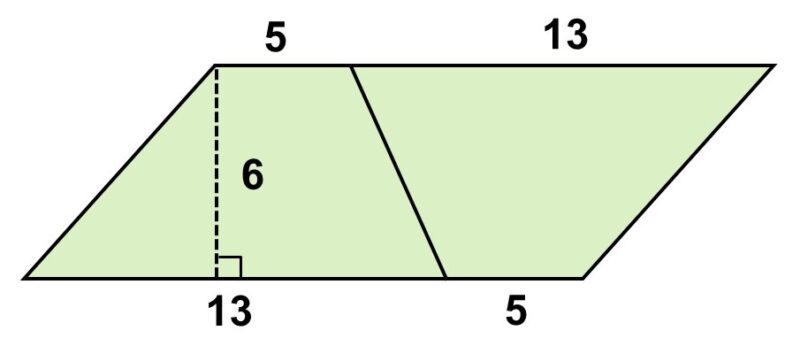
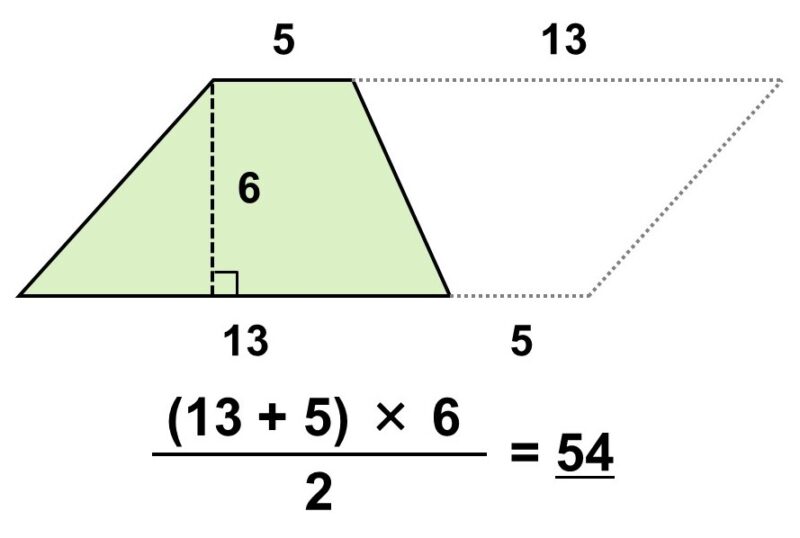
例えば、次の平行四辺形。正方形や長方形のように内角が90°ではないので、そのまま面積1の正方形に細かくするのは難しいです。
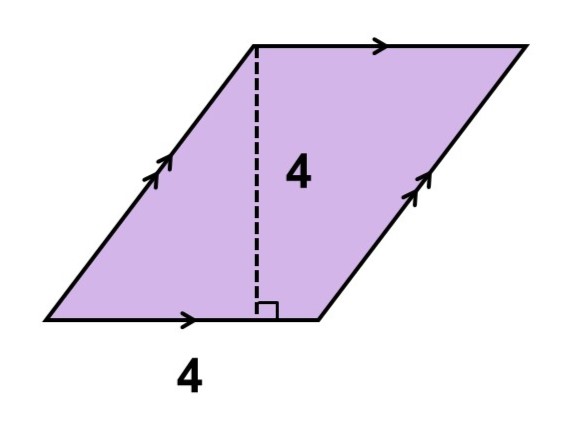
そこで、少し工夫をほどこしてみましょう。例えば、次のように真ん中で半分に切ってから隣にくっつけてみるとどうなるでしょうか？
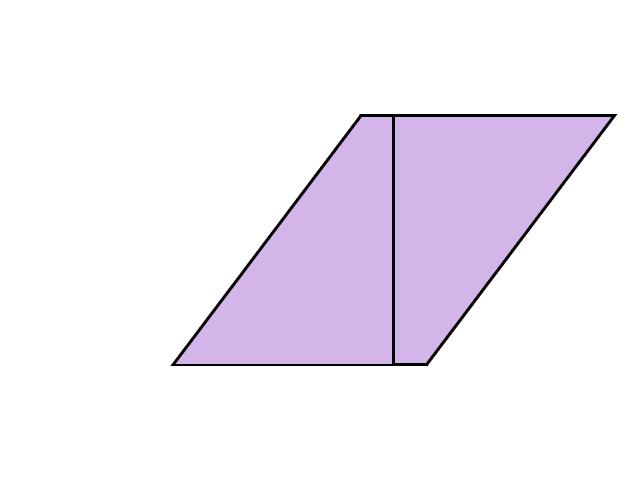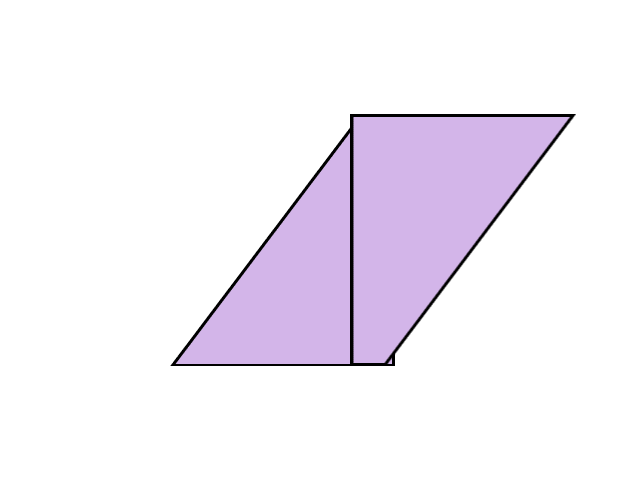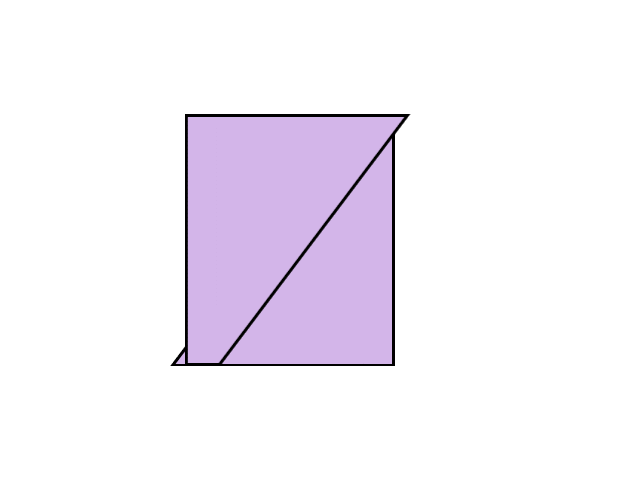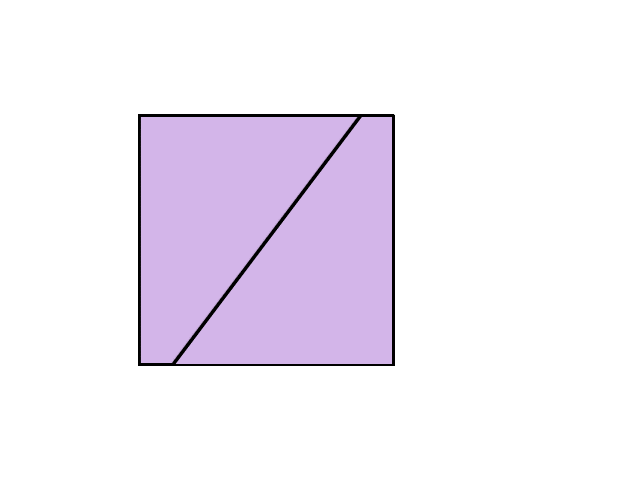
これはまさしく正方形ですね。半分にしてからもう一度くっつけたので、底辺と高さの長さも変わっていません。つまり、普通の正方形や長方形と同じように、底辺×高さで計算すればよいということです。
平行四辺形を正方形または長方形に直す方法はもう一つあります。
例えば先ほどの平行四辺形の場合、一組の対辺について、平行（高さ）を保ちながら動かしていくと、正方形にすることができます。
このような変形を等積変形（とうせきへんけい）といい、面積を変えずに図形を変形させる方法としてよく用いられます。
三角形の面積
あらゆる図形は三角形に分けることができるので、「三角形の面積が計算できる＝あらゆる図形の面積が計算できる」と言えます。そこで今度は、三角形の面積について考えてみます。
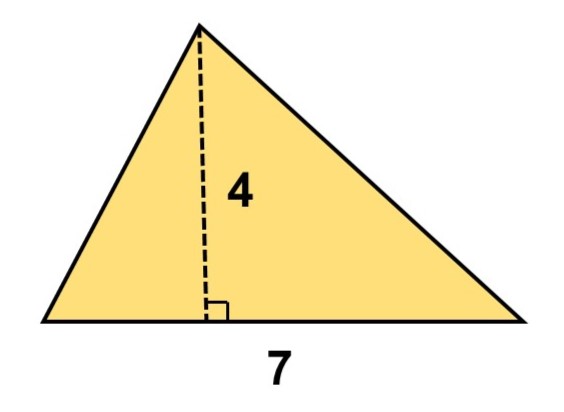
このままでは計算できないので、一度、計算方法がわかっている図形に落としこんで考えてみましょう。例えば、この三角形と合同な三角形を持ってきてくっつけるとどうなるでしょうか？
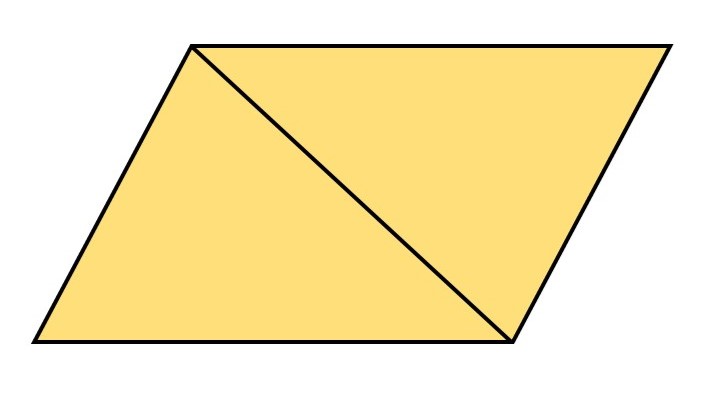
そう、平行四辺形になりますね。こんな時にも合同の考え方が役立ちます（くわしくは31F）。平行四辺形なら先ほど学んだ通り、底辺×高さで面積が計算できます。
この平行四辺形を作るのに、元の三角形を2つ使っているので、今求めた面積を半分にすれば面積が出ます。
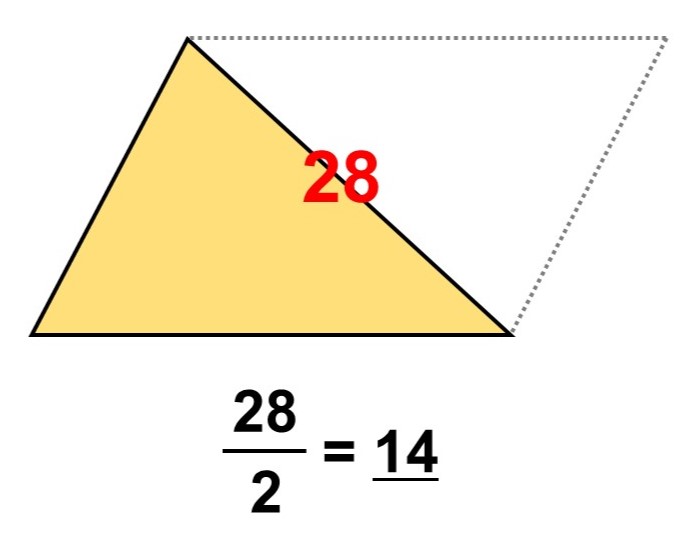
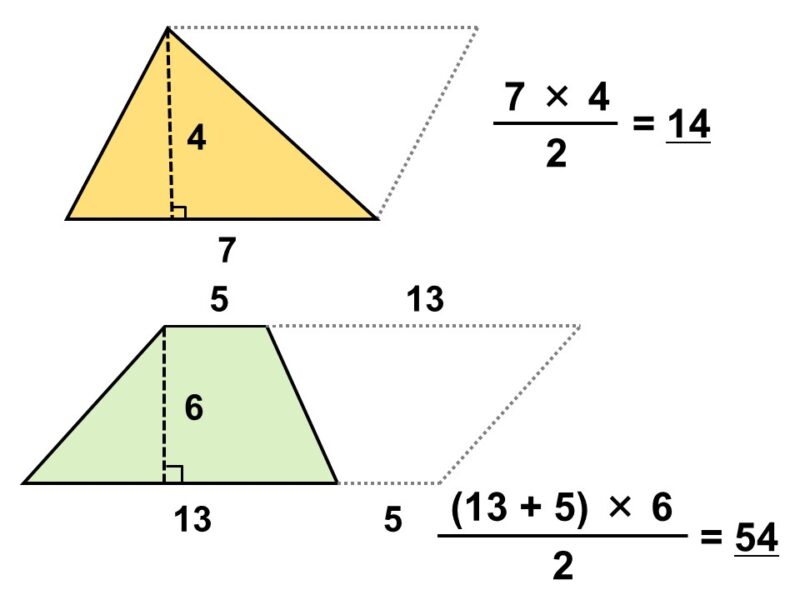
したがって、三角形の面積は平行四辺形の面積の半分、つまり底辺×高さ÷2で計算できます。
ここでもう一つ例題を見ておきましょう。三角形の高さはいつも最初からわかっているとは限りませんが、前回学んだ「三角比」を使えば、辺の長さと内角から高さを求めることができます。
（例）
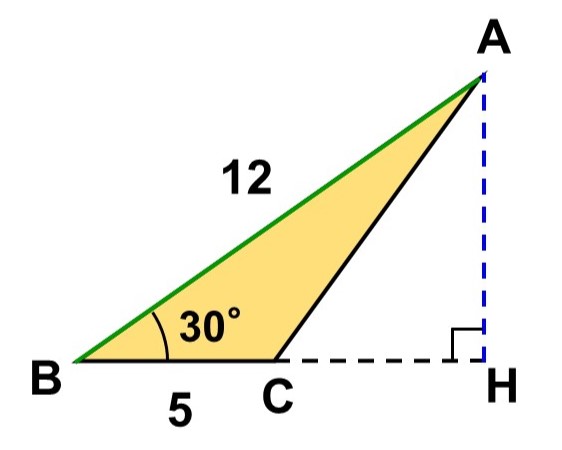
角$\mathrm{C}$を鈍角とする$\triangle \mathrm{ABC}$の面積を求めてみよう。
今、頂点$\mathrm{A}$から辺$\mathrm{ABC}$に向かって垂線$\mathrm{AH}$を下ろすと、$\triangle \mathrm{ABC}$の底辺は$\mathrm{BC}$、高さは$\mathrm{AH}$とみなせる。
直角三角形$\mathrm{ABH}$に注目すると、
$\begin{align}
\mathrm{AH} &= \mathrm{AB} \times \sin 30^{\circ} \\[1.5ex]
&= 12 \times 0.5 \\[1.5ex]
&= 6
\end{align}$
よって、$\triangle \mathrm{ABC}$の面積は
$\begin{align}
\dfrac{\mathrm{BC} \times \mathrm{AH}}{2} &= \dfrac{5 \times 6}{2} \\[1.5ex]
&= 15
\end{align}$
平行四辺形と似た図形に台形（だいけい）と呼ばれる図形があります。この図形は1組の対辺のみが平行な四角形です。
台形も三角形と同じような考え方で面積を求めることができます。すなわち、合同な台形をもう一つ持ってきてくっつけると平行四辺形ができます。
平行四辺形の面積がわかれば、あとはこれを半分にすれば、台形の面積がわかります。
台形の面積公式に「上底＋下底」という言葉が出てくるのは、2つの合同な台形からできる平行四辺形の底辺に由来しています。
面積から面積を求める方法 ― 面積比
ここまでで学んできたように、面積を求める時には、底辺・高さ・角度といった情報が必要になるわけですが、こうした情報がいつもわかっているとは限りません。
そこで役立つのが、面積比です。面積比さえわかれば、比率を使って面積から面積を求めることができます。実際、次に示すような場合であれば、面積比を簡単に調べることができます。
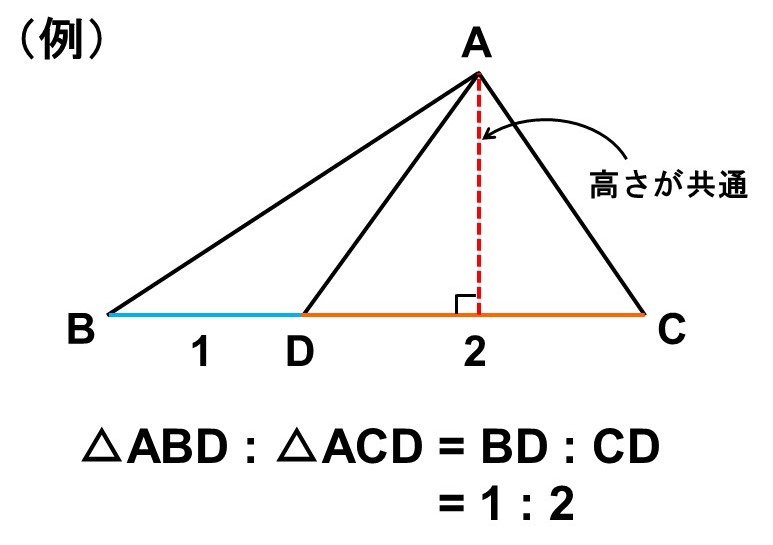
底辺または高さが等しい三角形の面積比
三角形の面積は平行四辺形の半分、すなわち
$\dfrac{\text{底辺} \times \text{高さ}}{2}$
で計算できます。
ということは、底辺が同じ場合、面積比は高さだけで決まります。
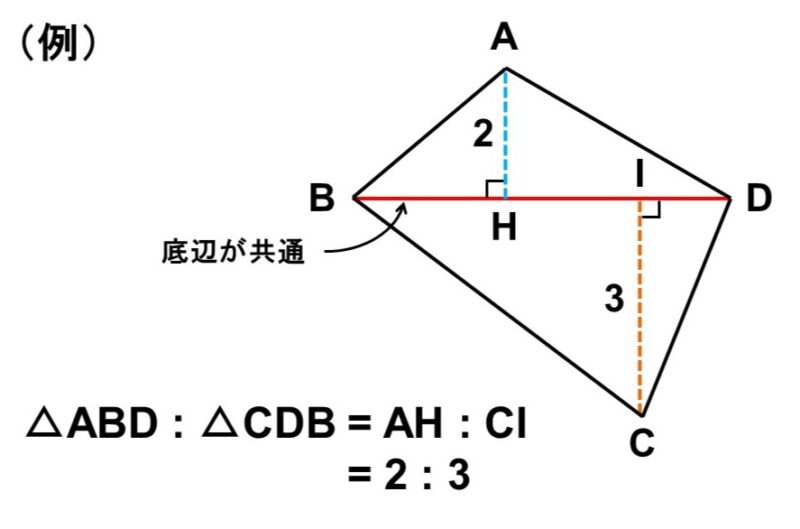
一方、高さが同じ場合、面積比は底辺だけで決まります。
相似な三角形の面積比
相似な三角形の面積比も調べるのは簡単です。
例として、相似比が5 : 2である2つの相似な三角形（$\triangle \mathrm{ABC}$, $\triangle \mathrm{ADE}$）の面積比を考えてみます。
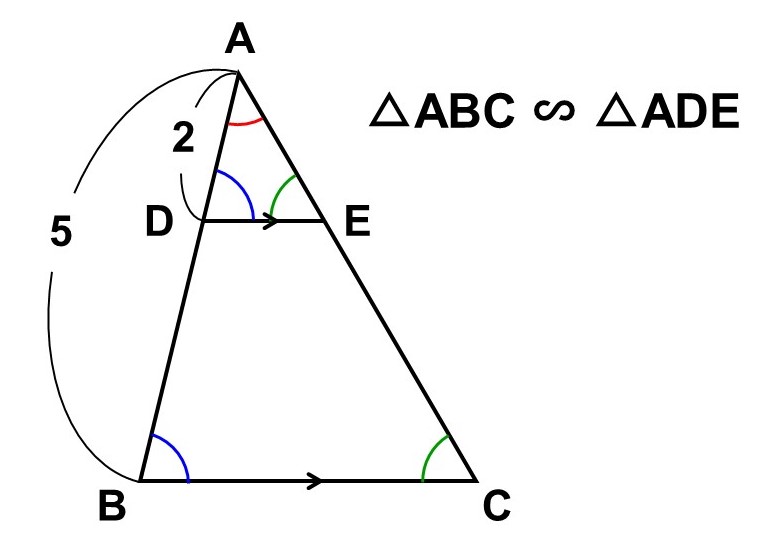
相似の基本性質は「対応する線分の比が常に等しい」です。つまり、$\triangle \mathrm{ABC}$と$\triangle \mathrm{ADE}$の底辺や高さが具体的な値としてわからないとしても、その比については同じ5 : 2になります。
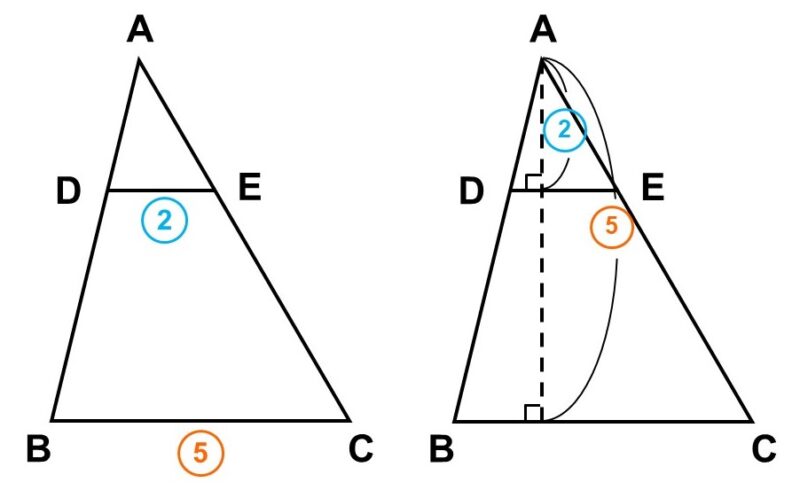
そして、三角形の面積は底辺×高さ÷2なので、面積比だけに注目すれば、
$\begin{align}
\triangle \mathrm{ABC} : \triangle \mathrm{ADE} &= \dfrac{5 \times 5}{2} : \dfrac{2 \times 2}{2} \\[1.5ex]
&= 5^2 : 2^2 = 25 : 4
\end{align}$
となります。このように、底辺と高さの両方で相似比を考えることになるので、面積比は相似比の2乗になります。
まとめ
今回は面積について学びました。内容をまとめると次のようになります。
- 面積とは、「1辺の長さが1の正方形」を基本単位として、その何個分になるかで図形の大きさを考える指標である。
- 正方形・長方形・平行四辺形の面積は、底辺×高さで求まる。
- 三角形・台形の面積は平行四辺形の半分として計算すればよい。
- 面積比を利用すると、図形に関する情報がなくても、比率から面積を求めることができる。
面積が掛け算で求まる理由、理解できたでしょうか？「小さな正方形を数えるイメージ」を忘れなければ、公式も納得しながら使うことができるはずです。
この階で、三角形をメインとした内容は一区切りになります。次回からは、平面図形におけるもう一つの主役である円について学んでいきます！
今回はここまでです。お疲れさまでした！
