こんにちは、まてがめです。
前回は「円の外側」で成り立つ図形の性質として、内心・傍心について学びました。
今回からは「円の内側」で成り立つ図形の性質を学んでいきます。こちらは3部構成になっており、第1部である今回は、内心・傍心と並んで有名な外心・垂心について学びます。
特に外心は、前回学んだ内心・傍心と同じく、三角形と円を結びつける重要なものです。この記事を読んで、三角形と円の関係性をより深く理解していきましょう!
外心
外心とは?
円周上に3点をとれば、円の内部に三角形を描くことができます。
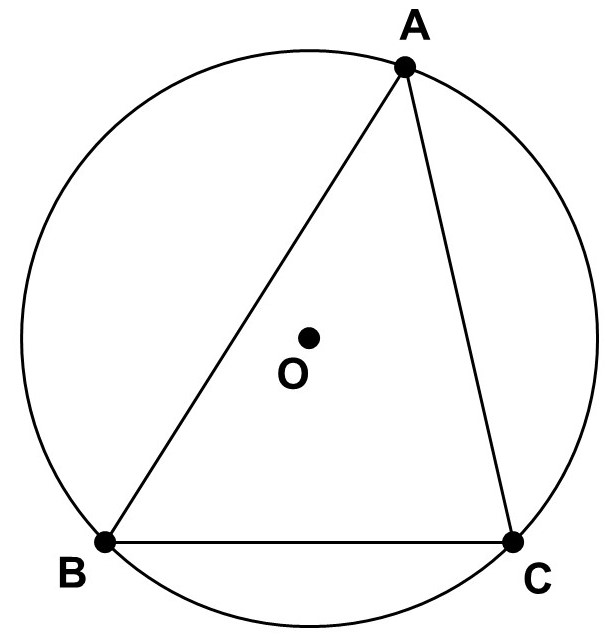
前回は三角形の中で接する円(内接円)について紹介しましたが、こちらは三角形の外で円が接しているので外接円(がいせつえん)と呼ばれます。また、外接円の中心を外心(がいしん)といい、通常の円の中心と同じように$\mathrm{O}$で表します。
垂直二等分線は外心で交わる
では、内心について考えたときと同じように、三角形と外接円の関係について考えてみましょう。
まず、$\mathrm{OA}$, $\mathrm{OB}$, $\mathrm{OC}$は円$\mathrm{O}$の半径にあたるので、$\mathrm{O}$を頂点とする3つの二等辺三角形($\triangle \mathrm{OAB}$, $\triangle \mathrm{OBC}$, $\triangle \mathrm{OCA}$)を見つけることができます。
二等辺三角形は頂点から底辺に向かって垂直二等分線が引くことができます(これも三角形の合同から生まれる性質でしたね)。つまり、$\mathrm{O}$から$\mathrm{AB}$, $\mathrm{BC}$, $\mathrm{CA}$に向かって垂直二等分線が引けます。
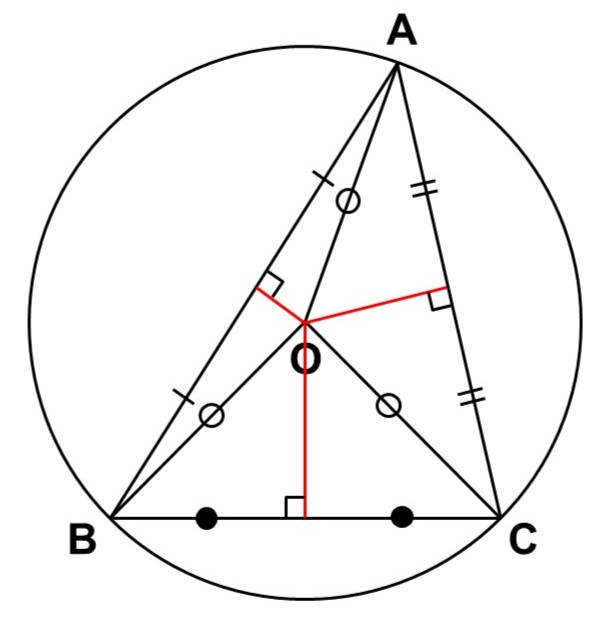
ところで、$\mathrm{AB}$, $\mathrm{BC}$, $\mathrm{CA}$はもともと$\triangle \mathrm{ABC}$の辺なので、逆に考えれば、$\triangle \mathrm{ABC}$の各辺において垂直二等分線を引けば、外心を見つけることができるとも言えます。
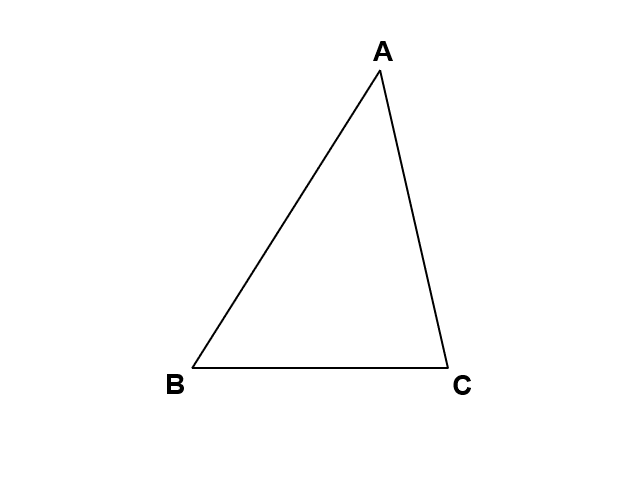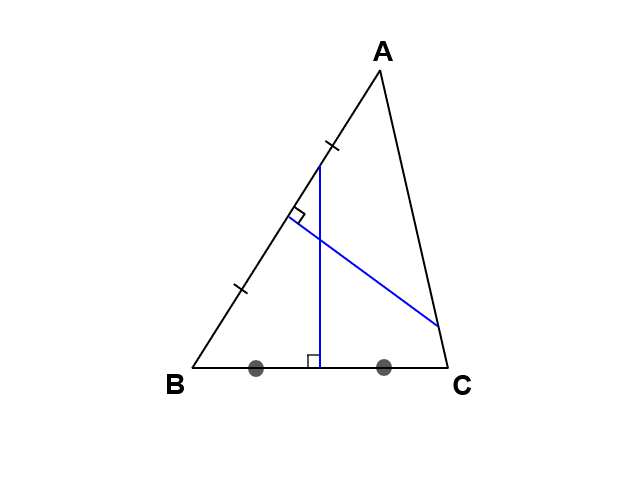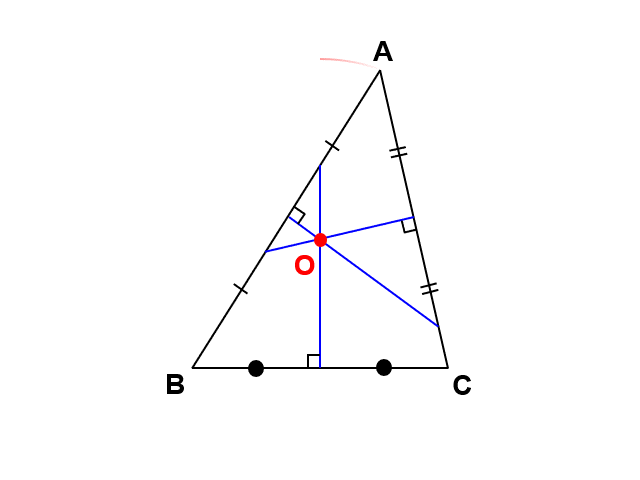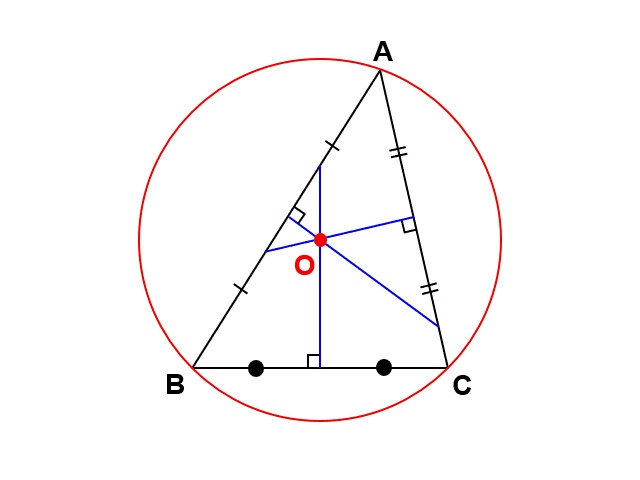
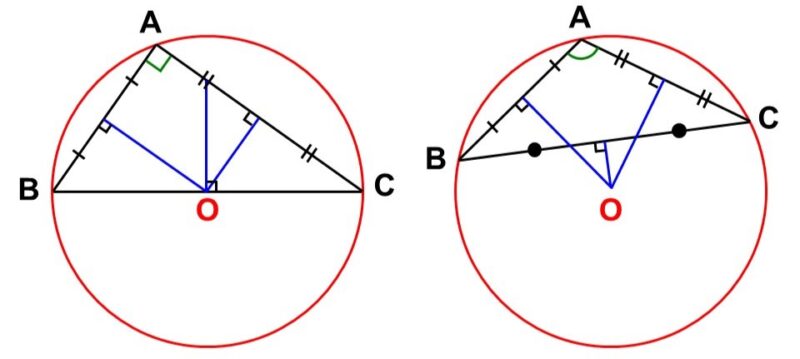
これはすなわち、あらゆる三角形において外心が存在するということです。この例では鋭角三角形でしたが、直角三角形や鈍角三角形でも、やはりこの方法で外心を見出すことができます。
(例)
$B = 90^{\circ}$, $\mathrm{AB} = 3$, $\mathrm{BC} = 4$, $\mathrm{CA} = 5$の直角三角形$\mathrm{ABC}$がある。この外接円の半径を求めてみよう。
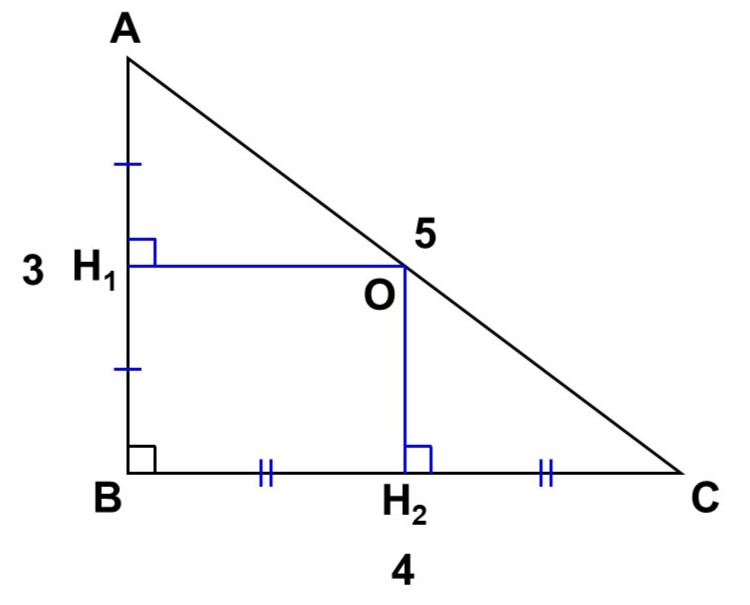
辺$\mathrm{AB}$, $\mathrm{BC}$において垂直二等分線を引き、交点(外接円の中心)を$\mathrm{O}$とする。また、垂直二等分線の足をそれぞれ$\mathrm{H_1}$, $\mathrm{H_2}$とする。
すると、四角形$\mathrm{H_{1}BH_{2}O}$は長方形なので、対辺が等しく、
$\mathrm{H_{1}B} = \mathrm{OH_{2}}$ <1>
$\mathrm{H_{1}O} = \mathrm{BH_{2}}$ <2>
ここで、$\triangle \mathrm{AH_{1}O}$と$\triangle \mathrm{OH_{2}C}$について次のことが言える。
- $\angle \mathrm{AH_{1}O} = \angle \mathrm{OH_{2}C} = 90^{\circ}$ <3>
- <1>より、$\mathrm{AH_{1}} = \mathrm{H_{1}B} = \mathrm{OH_{2}}$ <4>
- <2>より、$\mathrm{H_{1}O} = \mathrm{BH_{2}} = \mathrm{H_{2}C}$ <5>
<3>, <4>, <5>より、$\triangle \mathrm{AH_{1}O}$と$\triangle \mathrm{OH_{2}C}$は2辺とその間の角がそれぞれ等しいので合同である。
したがって、対応する角が等しく、
$\angle \mathrm{H_{1}OA} = \angle \mathrm{H_{2}CO} = \alpha$ <6>
$\angle \mathrm{OAH_{1}} = \angle \mathrm{COH_{2}} = \beta$ <7>
と表せる。なお、<3>に示すように$\triangle \mathrm{AH_{1}O}$、$\triangle \mathrm{OH_{2}C}$における残りの角は直角なので、次が成り立っている。
$\alpha+\beta = 90^{\circ}$ <8>
ここで$\angle \mathrm{AOC}$について考えると、四角形$\mathrm{H_{1}BH_{2}O}$が長方形であることと<6>, <7>, <8>より、
$\begin{align}
&\hspace{13pt} \angle \mathrm{AOC} \\[1.5ex]
&= \angle \mathrm{H_{1}OA}+\angle \mathrm{H_{1}OH_{2}}+\angle \mathrm{COH_{2}} \\[1.5ex]
&= \alpha+90^{\circ}+\beta \\[1.5ex]
&= 90^{\circ}+90^{\circ} = 180^{\circ}
\end{align}$
これより、$\mathrm{A}$, $\mathrm{O}$, $\mathrm{C}$は同一直線上にあり、$\mathrm{AC}$は外接円$\mathrm{O}$の直径であることが言える。
よって、求める半径は
$\mathrm{OA} = \dfrac{\mathrm{AC}}{2} = \dfrac{5}{2}$
垂心
垂心とは?
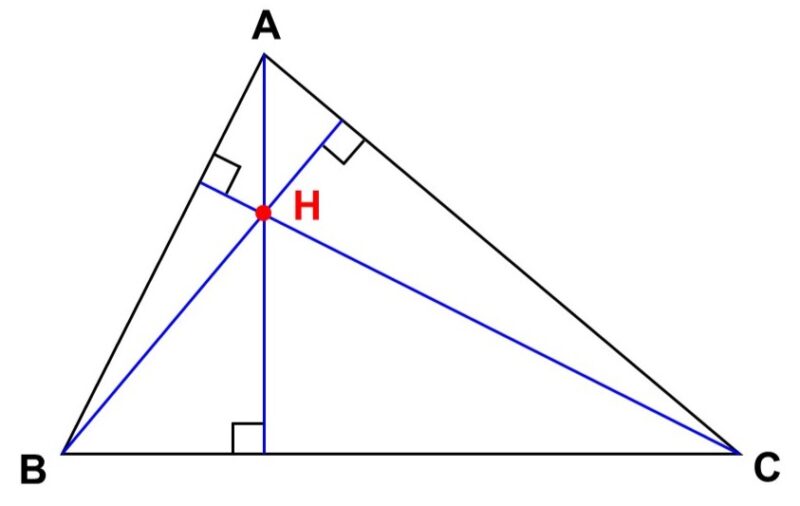
外心と関連するものに、垂心(すいしん)があります。これは三角形の各頂点から底辺に向かって下ろした時にできる垂線の交点のことで、$\mathrm{H}$で表すことが多いです。外心と同じく垂心についても、あらゆる三角形が持っています。
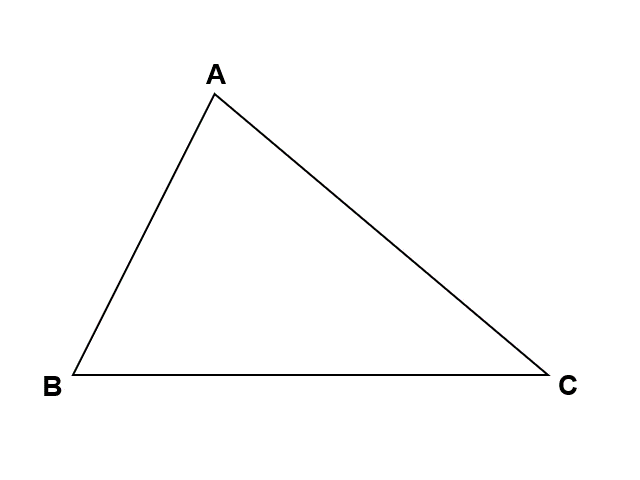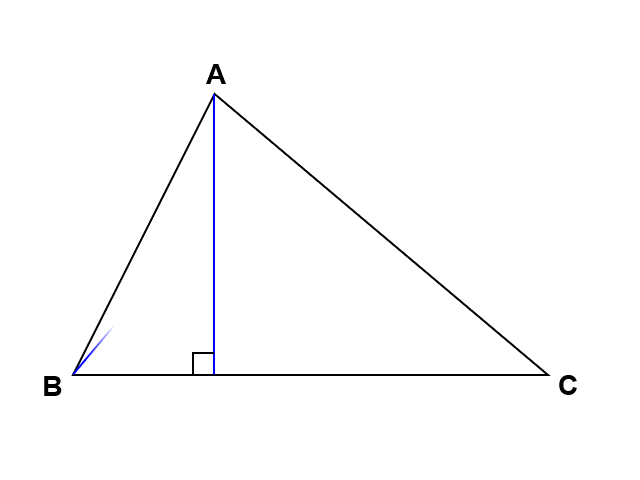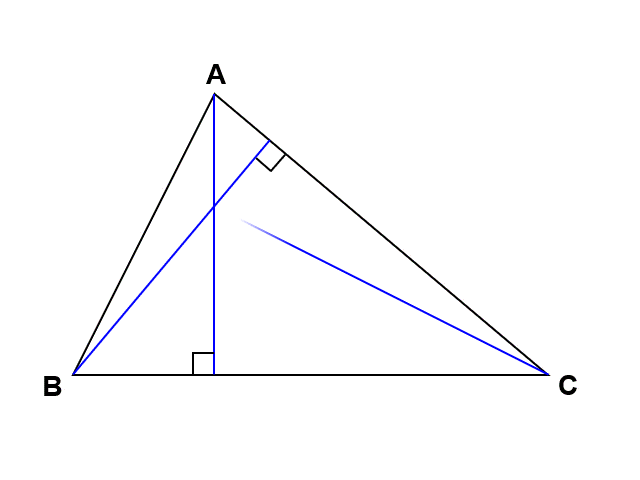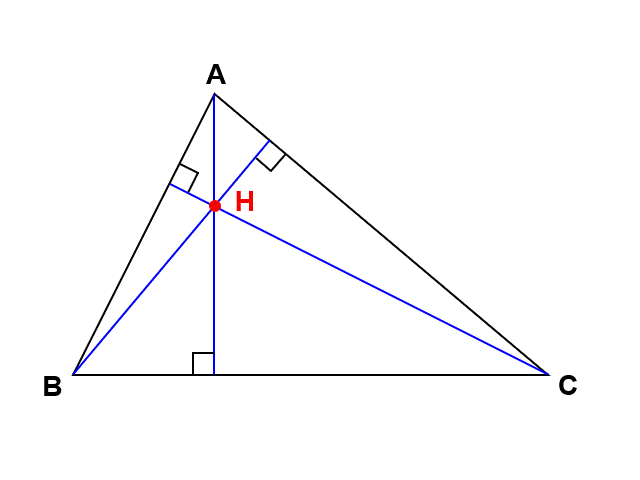
これを聞いて最初に疑問に思うのが、「そんな毎回都合よく3本の垂線が交わるなんてことがありえるのか?」ということです。まてがめも初めはそう思っていました。
垂心の存在を証明してみよう
では、三角形の頂点から引く垂線が1点で交わることを証明してみます[1]。この証明を見れば、垂心と外心の関係性がよくわかります。
(命題)
任意の三角形$\triangle \mathrm{ABC}$において、各頂点から底辺に向かって下ろした垂線は1点(垂心)で交わる。
(証明)
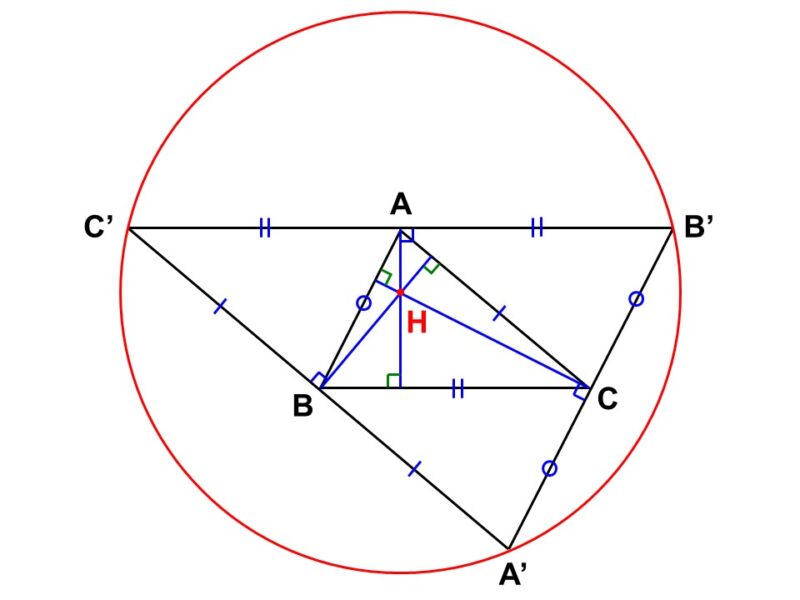
頂点$\mathrm{B}$, $\mathrm{C}$から底辺$\mathrm{CA}$, $\mathrm{AB}$に垂線$\mathrm{BP}$, $\mathrm{CQ}$を下ろし、交点を$\mathrm{H}$とする。
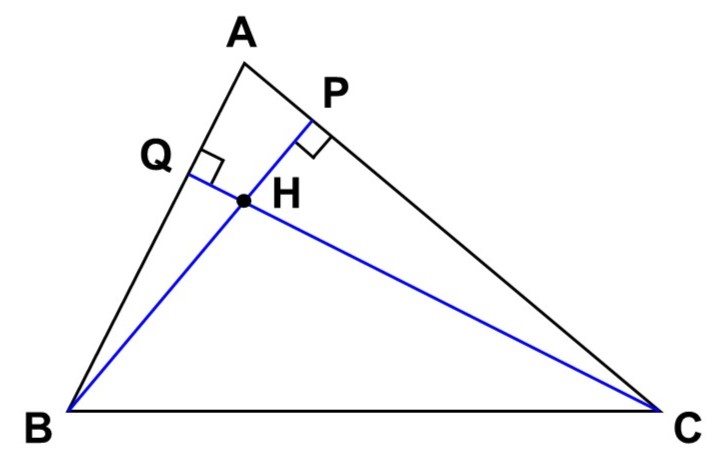
次に、$\mathrm{A}$を通って$\mathrm{BC}$に平行な直線、$\mathrm{B}$を通って$\mathrm{CA}$に平行な直線、$\mathrm{C}$を通って$\mathrm{AB}$に平行な直線を引き、新たに$\triangle \mathrm{A’B’C’}$を作る。
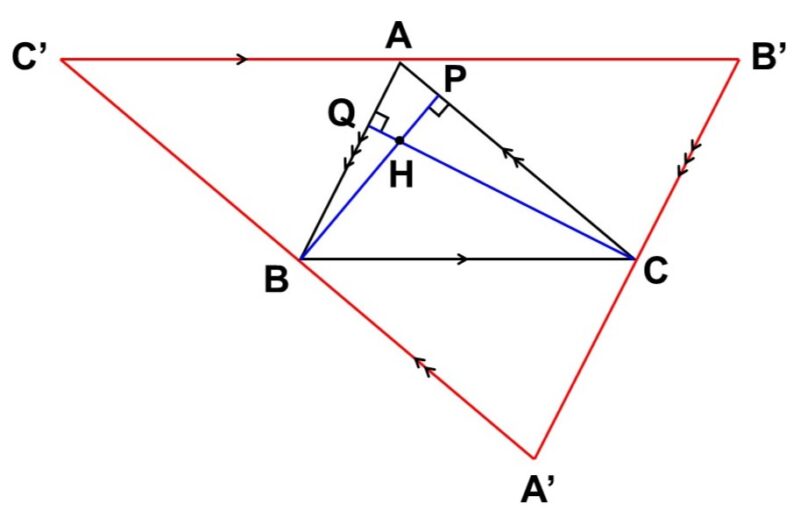
すると、四角形$\mathrm{A’CAB}$, $\mathrm{B’ABC}$, $\mathrm{C’BCA}$は平行四辺形なので、対辺がそれぞれ等しく、
$\mathrm{C’B} = \mathrm{BA’} = \mathrm{AC}$
$\mathrm{A’C} = \mathrm{CB’} = \mathrm{BA}$
$\mathrm{B’A} = \mathrm{AC’} = \mathrm{CB}$
すなわち、$\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$はそれぞれ$\mathrm{B’C’}$, $\mathrm{C’A’}$, $\mathrm{A’B’}$の中点である。
また、錯角が等しいので、
$\angle \mathrm{A’BP} = \angle \mathrm{APB} = 90^{\circ}$
$\angle \mathrm{B’CQ} = \angle \mathrm{BQC} = 90^{\circ}$
以上より、$\mathrm{BP}$, $\mathrm{CQ}$はそれぞれ$\mathrm{C’A’}$, $\mathrm{A’B’}$の垂直二等分線であり、その交点$\mathrm{H}$は$\triangle \mathrm{A’B’C’}$の外心にあたる。
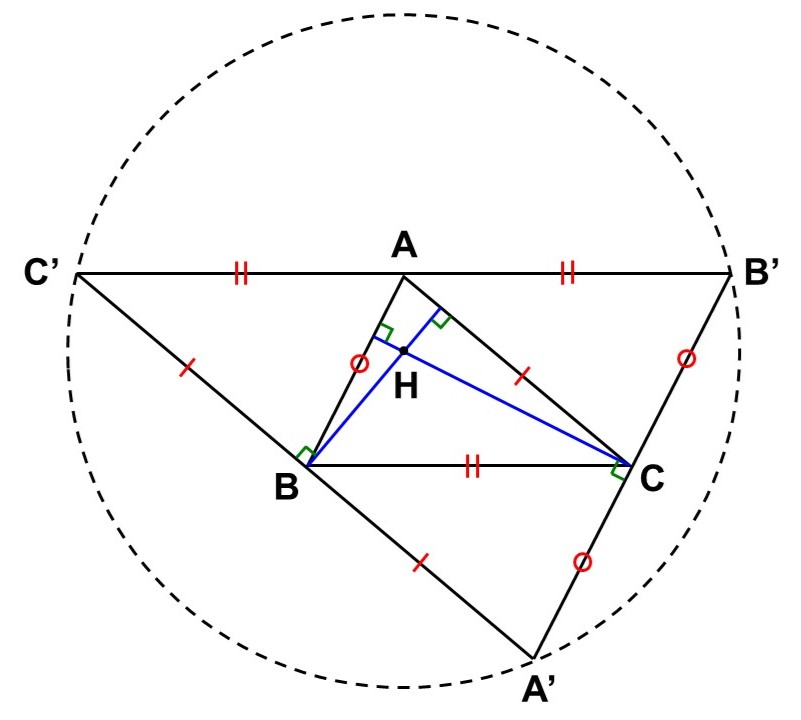
したがって、$\mathrm{B’C’}$の垂直二等分線は中点$\mathrm{A}$と外心$\mathrm{H}$を通る。この垂直二等分線と$\mathrm{BC}$の交点を$\mathrm{R}$とすると、錯角が等しいので、
$\angle \mathrm{C’AR} = \angle \mathrm{CRA} = 90^{\circ}$
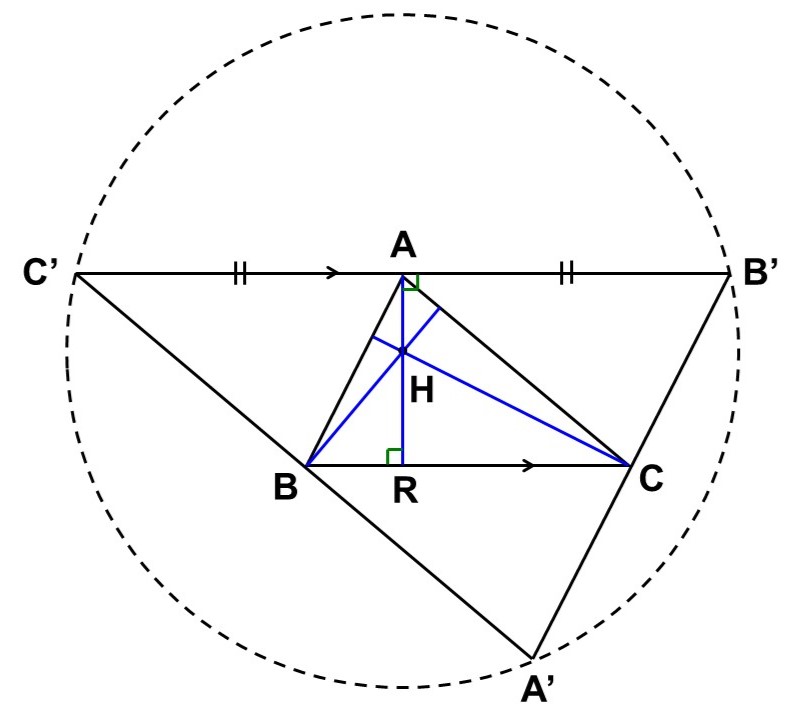
つまり、$\mathrm{AR}$は$\mathrm{BC}$の垂線である。
以上より、
- $\mathrm{AR}$が$\mathrm{H}$を通る
- $\mathrm{AR} \perp \mathrm{BC}$
が言えたので、命題が真であることが示せた。
(証明終)
このように、垂心が存在することは、その外側にできる三角形の外心と一致することによって保証されています。
※同じ三角形に対する外心と垂心が一致するという意味ではないので、勘違いしないようにしましょう。
まとめ
今回は外心・垂心について学びました。まとめると次の通りです。
- $\triangle \mathrm{ABC}$の各辺において垂直二等分線を引くと1点で交わる。これを外心といい、外心を中心として$\triangle \mathrm{ABC}$に接する円(外接円)が描ける。
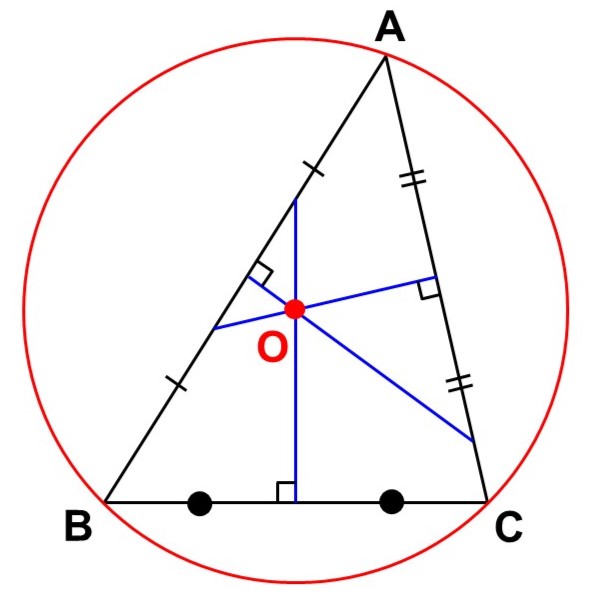
- $\triangle \mathrm{ABC}$の各頂点から対辺に向かって垂線を下ろすと1点で交わる。これを垂心という。垂心は、頂点を通って各対辺に平行な直線からなる三角形の外心と一致する。
前回紹介した内心・傍心、今回紹介した外心・垂心、そして重心(練習問題の方で解説します)の5つは「三角形の五心」と呼ばれており、三角形における重要な性質として知られています。
それぞれがどのように作図できるのか、それを起点としてどんな性質があるのかについてはよく理解しておきましょう。
今回はここまでです。お疲れ様でした!
参考資料
[1] チャート式 基礎からの数学Ⅰ+A 新課程 (チャート研究所 / 数研出版 2022)