こんにちは、まてがめです。
前回は、三角形に並ぶ平面図形の主役「円」について学びました。
この階で解説したように、円は対称性が高く、美しい図形です。そのため、図形が円とかかわりを持つような状況になると、例えば次のような面白い性質が表に出てきます。
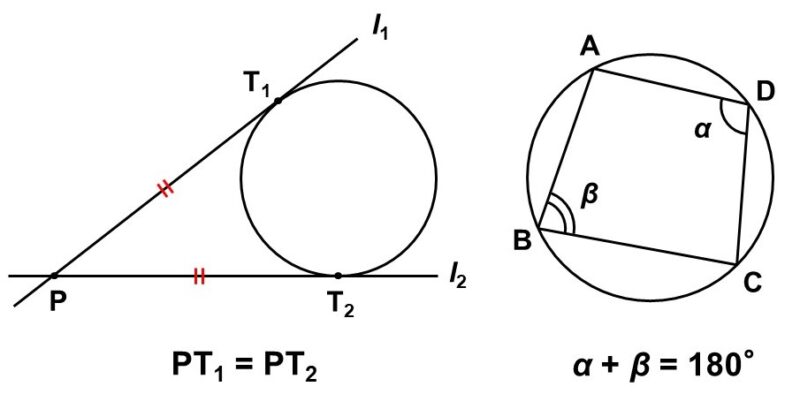
よく使う重要な性質だけにしぼっても、内容がかなり盛りだくさんなので、前編（この階）では「円の外側」、後編（36F）では「円の内側」に注目して、その図形的な性質を学んでいくことにします。
さて、今回は「円の外側」に注目していくわけですが、この時カギとなるのが31Fで学んだ「合同」です。
確かに円は三角形と見た目も形も異なる図形ですが、実は「三角形の合同」を通して、今回紹介する「内心」や「傍心」といった形で三角形と密接につながっています。
接線と接点
まずは、円と直線から生まれる関係性について見ていきましょう。
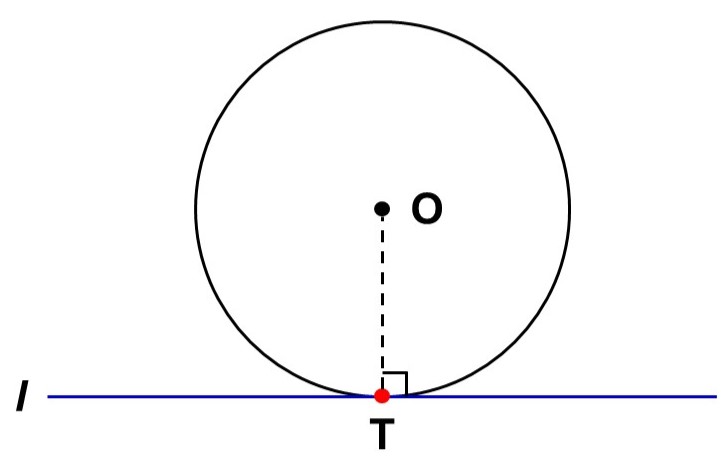
円の中心$\mathrm{O}$から直線$l$までの（最短）距離がちょうど円の半径に等しい時、円と直線はただ1つの共有点$\mathrm{T}$を持ちます。このような時、「直線$l$は円$\mathrm{O}$に接する」といいます。
またこの時、円$\mathrm{O}$に対して、直線$l$を接線（せっせん）、点$\mathrm{T}$を接点（せってん）といい、接線$l$と線分$\mathrm{OT}$は垂直に交わります。
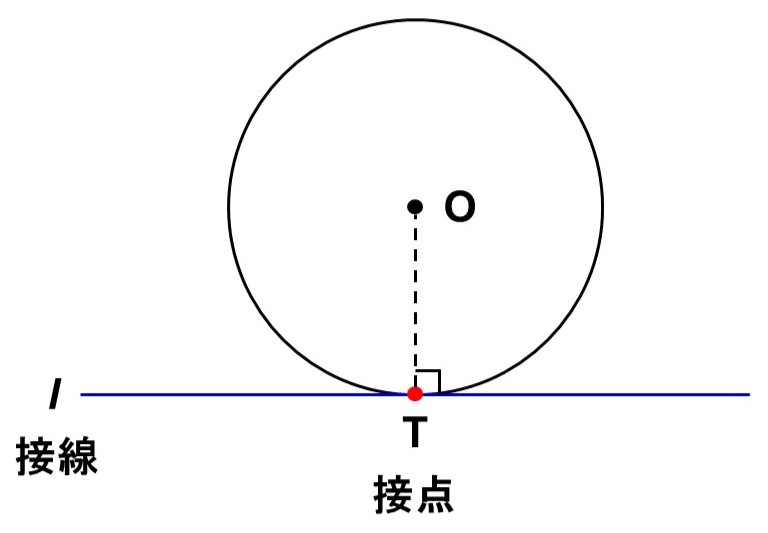
本当に円と直線は「接する」のか？
図を見れば、多くの方が「確かに円と直線は接する場合があるな」と納得してくれるはずです。しかし、まてがめは心配性なので、こんな疑問が出てきます。
「円の中心と直線の距離が半径に等しいとして、本当に円と直線は1点だけで交わる（接する）のか？」
そこで、これをきちんと証明してみようと思います。今回は背理法（誤った仮定から出発して矛盾を示す証明方法）を用いた方法を紹介します[1]。
（命題）
円の中心$\mathrm{O}$から直線$l$までの距離が半径に等しい時、円$\mathrm{O}$と直線$l$はただ一つの共有点$\mathrm{T}$を持つ（接する）。
（証明）
円$\mathrm{O}$と直線$l$が点$\mathrm{T}$の他に、もう一つの共有点$\mathrm{T’}$を持つと仮定する。
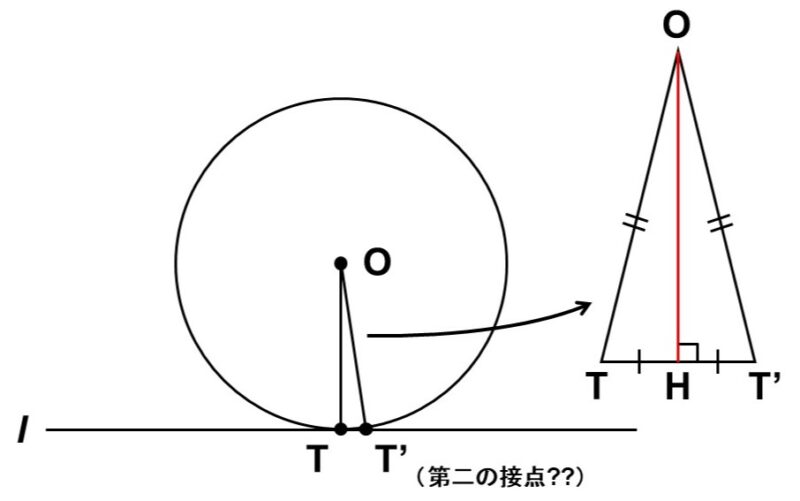
この時、$\mathrm{T}$, $\mathrm{T’}$はどちらも円$\mathrm{O}$上の点なので、
$\mathrm{OT} = \mathrm{OT’}$
したがって、$\triangle \mathrm{OTT’}$は二等辺三角形なので、頂点$\mathrm{O}$から底辺$\mathrm{TT’}$に向かって垂直二等分線$\mathrm{OH}$を引くことができる。
一方、$\mathrm{T}$, $\mathrm{T’}$はどちらも直線$l$上の点であり、線分$\mathrm{TT’}$は直線$l$の一部である。つまり、線分$\mathrm{TT’}$上の点$\mathrm{H}$もまた直線$l$上の点である。
ここで$\triangle \mathrm{OTH}$に注目すると、これは$\angle \mathrm{THO} = 90^{\circ}$の直角三角形である。よって、角と対辺の大小関係から
$\angle \mathrm{THO} > \angle \mathrm{OTH} \iff \mathrm{OT} > \mathrm{OH}$
すなわち、直線$l$上の点$\mathrm{H}$は円$\mathrm{O}$の内部にあることになる。しかしこれは、円の中心$\mathrm{O}$と直線$l$の距離が半径に等しいことに矛盾する。
よって、仮定は誤りであり、円$\mathrm{O}$と直線$l$はただ一つの共有点$\mathrm{T}$のみを持つ。
（証明終）
こうして円と直線が「接する」という状況を正しく理解することができました。
本当に接線は半径に対して垂直？
これでもう安心…かと思ったのですが、それもつかの間。新たな不安がわいてきました。それは「直線$l$と線分$\mathrm{OT}$は本当に垂直なのか？」ということです。
「そんなのどう見てもそうだろ！」といろんな方からツッコまれそうですが、章の初めでも言ったように幾何学は理論の積み上げがかなめですから、一応これも証明しておきましょう。こちらも背理法を使った証明が知られています[1]。
（命題）
半径$r$の円$\mathrm{O}$と直線$l$が点$\mathrm{T}$で接する時、$l \perp \mathrm{OT}$が成り立つ。
（証明）
直線$l$と線分$\mathrm{OT}$は垂直に交わっていないと仮定する。
この時、$\mathrm{O}$から直線$l$に向かって垂線$\mathrm{OH}$を下ろすことができる。また、直線$l$上に、$\mathrm{HT} = \mathrm{HT’}$となるように点$\mathrm{T’}$をとることができる。
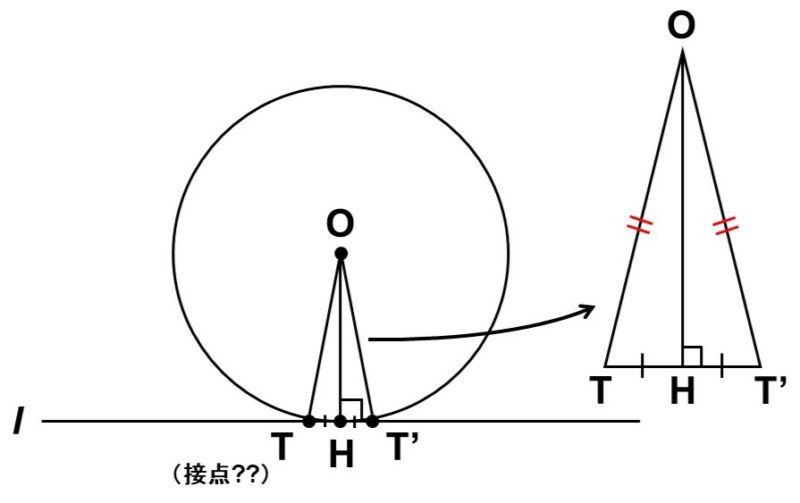
すると、線分$\mathrm{OH}$は線分$\mathrm{TT’}$の垂直二等分線になっているので、$\triangle \mathrm{OTT’}$は$\mathrm{OT} = \mathrm{OT’}$の二等辺三角形である。
しかし、これは点$\mathrm{T’}$も円$\mathrm{O}$上にあることを意味しており、$\mathrm{T}$が接点（円$\mathrm{O}$と直線$l$のただ一つの共有点）であることに矛盾する。
よって、仮定は誤りであり、$l \perp \mathrm{OT}$が成り立つ。
（証明終）
長くなりましたが、これでようやく円と直線が「接する」ということの意味を確認できました。当たり前に思えることほど証明するのも難しい…！
内心と傍心
円外の点を通る接線
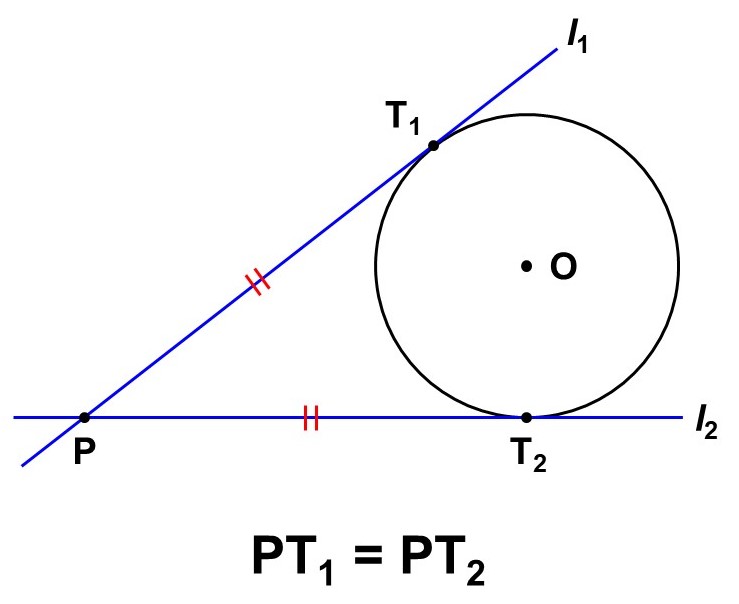
ここまでは円と1本の直線が接する場合を見てきましたが、円$\mathrm{O}$の外にある点$\mathrm{P}$を通るような接線を引く場合、接線は最大で2本（$l_1$, $l_2$）引くことができます。
この時の接点をそれぞれ$\mathrm{T_1}$, $\mathrm{T_2}$とすると、実は点$\mathrm{P}$からこれら2点までの距離は等しくなります。
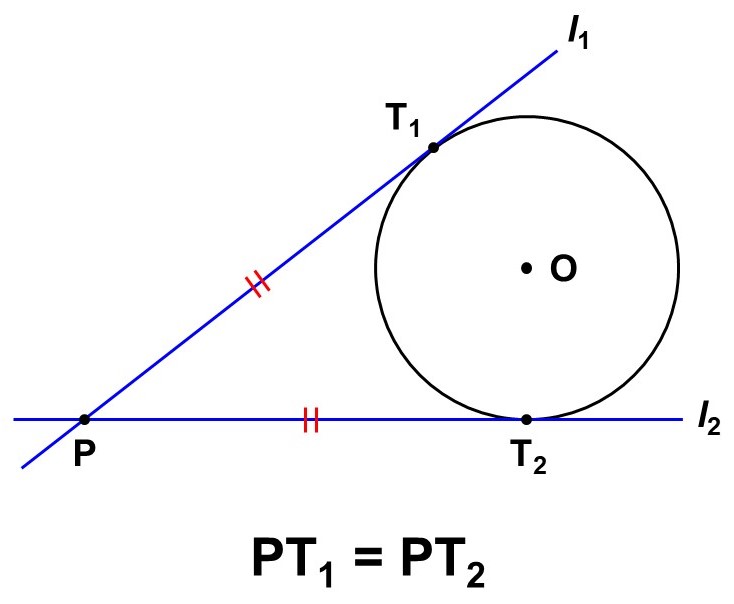
なぜこんなことが成り立つのでしょうか？これは「三角形の合同」を使うと簡単に確かめることができます。
（命題）
円$\mathrm{O}$の外にある点$\mathrm{P}$から接線$l_1$, $l_2$を引き、接点をそれぞれ$\mathrm{T_1}$, $\mathrm{T_2}$とする。この時、$\mathrm{PT_1} = \mathrm{PT_2}$が成り立つ。
（証明）
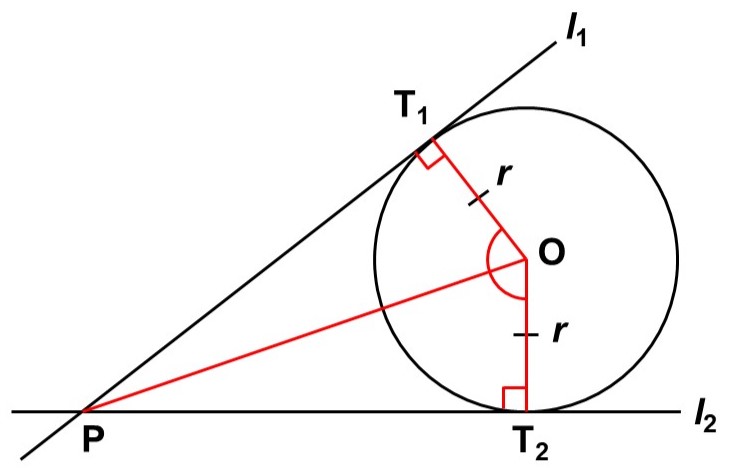
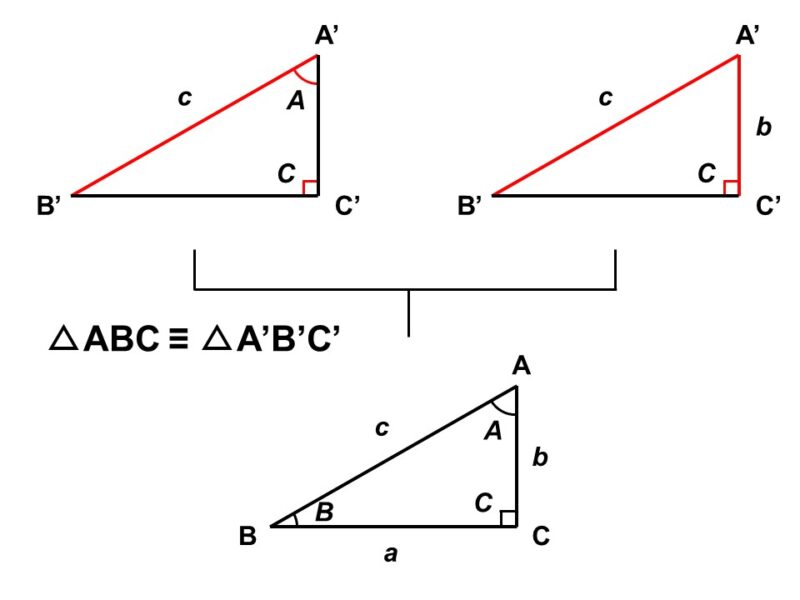
$\triangle \mathrm{OPT_1}$と$\triangle \mathrm{OPT_2}$に注目すると、次のことが言える。
- $\mathrm{OP}$が共通している …<1>
- $\mathrm{T_1O} = \mathrm{T_2O}$（半径） …<2>
- $\angle \mathrm{PT_{1}O} = \angle \mathrm{PT_{2}O} = 90^{\circ}$ …<3>
- 円$\mathrm{O}$の半径を$r$とすると、<1>, <2>, <3>より、
$\begin{align}
&\hspace{27pt} \sin \angle \mathrm{OPT_1} = \sin \angle \mathrm{OPT_2} = \dfrac{r}{\mathrm{OP}} \\[1.5ex]
&\iff \angle \mathrm{OPT_1} = \angle \mathrm{OPT_2}
\end{align}$
…<4>
<1>, <2>, <4>より、2辺とその間の角がそれぞれ等しいので、$\triangle \mathrm{OPT_1} \equiv \triangle \mathrm{OPT_2}$である。
よって対応する辺は等しいので、$\mathrm{PT_1} = \mathrm{PT_2}$が成り立つ。
（証明終）
三角形の合同条件については31Fで解説しましたが、ここで一度おさらいしておきます。
- 1辺とその両端の角がそれぞれ等しい
- 2辺とその間の角がそれぞれ等しい
- 3辺がそれぞれ等しい
合同が成り立つ時は必ずこれらのいずれかに当てはまるのですが、今回のように直角三角形について考える場合、すでに1つの角が90°と決まっているため、もっとシンプルな条件で合同を判断することができます。
2つの直角三角形が合同である時、次のどちらかが成り立っています。
- 斜辺と1つの角がそれぞれ等しい
- 斜辺と他の1辺がそれぞれ等しい
三角形の内角の和は180°ですから、1つ目の条件は「1辺とその両端の角がそれぞれ等しい」と中身は同じです。
一方、2つ目の条件は先ほどの証明で用いた「2辺とその間の角がそれぞれ等しい」に対応しています（三角比から示すことができます）。
ここで用いた「三角形の合同」は、次に説明する内心の理解にそのままつながっていきます。
内心
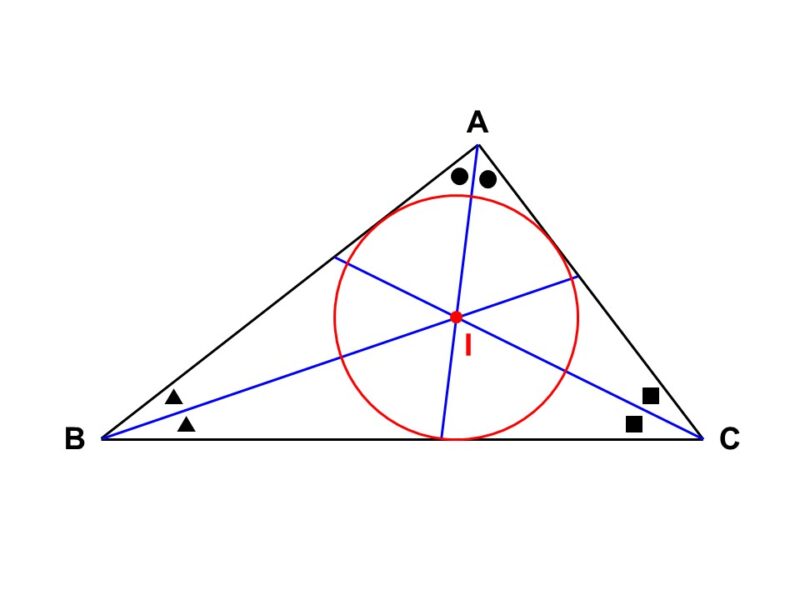
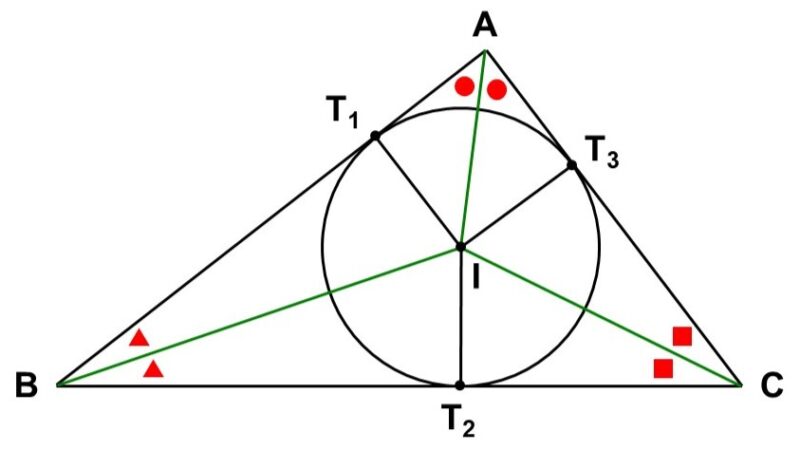
円$\mathrm{O}$に2本の直線$l_1$, $l_2$が接している先ほどの図において、第3の接線$l_3$を引くと、円$\mathrm{O}$を$\triangle \mathrm{ABC}$の中に閉じこめることができます。
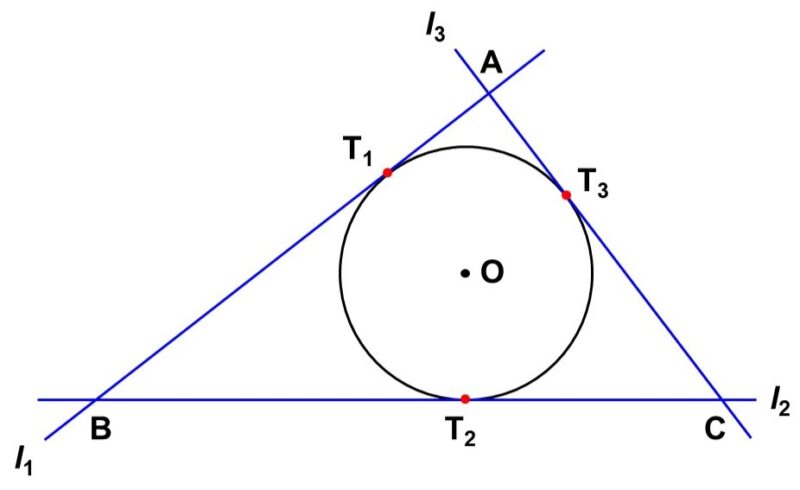
このように三角形の内側で接している（内接している）円を内接円（ないせつえん）といいます。また、内接円の中心は内心（ないしん）とも呼ばれ、「内側」を意味する”IN”の頭文字$\mathrm{I}$で表されることが多いです。
先ほどの証明で確認したように、円の外にある点から接線を引くと合同な三角形があらわれます。そのため、三角形に円が内接している場合においても、合同な三角形の組合せを見つけることができます。
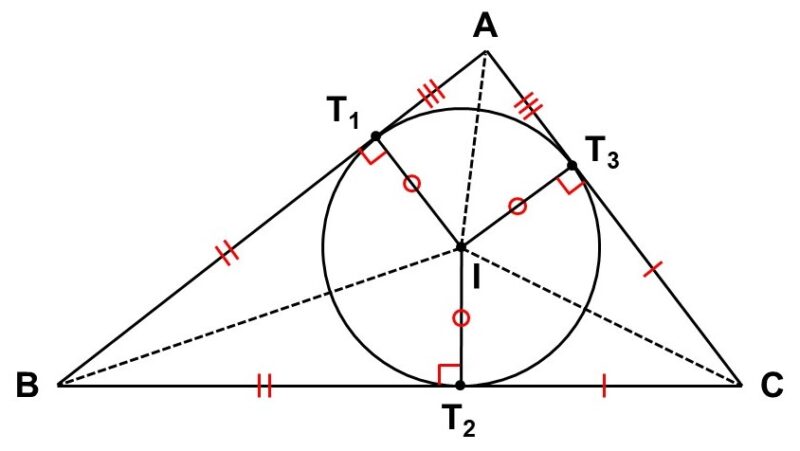
この図では、次の3組の合同を見出すことができます。
- $\triangle \mathrm{AT_{1}I} \equiv \triangle \mathrm{AT_{3}I}$
- $\triangle \mathrm{BT_{1}I} \equiv \triangle \mathrm{BT_{2}I}$
- $\triangle \mathrm{CT_{2}I} \equiv \triangle \mathrm{CT_{3}I}$
ところで、合同な三角形においては対応する角が等しいですから、$\mathrm{AI}$, $\mathrm{BI}$, $\mathrm{CI}$はちょうど角の二等分線になっていることもわかります。
ということは逆に、「$\triangle \mathrm{ABC}$の頂点で角の二等分線を引けば、内心$\mathrm{I}$を見つけることができる」とも考えることができないでしょうか？
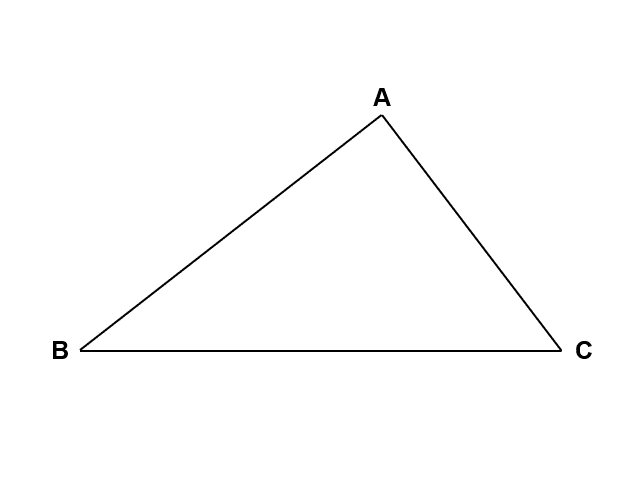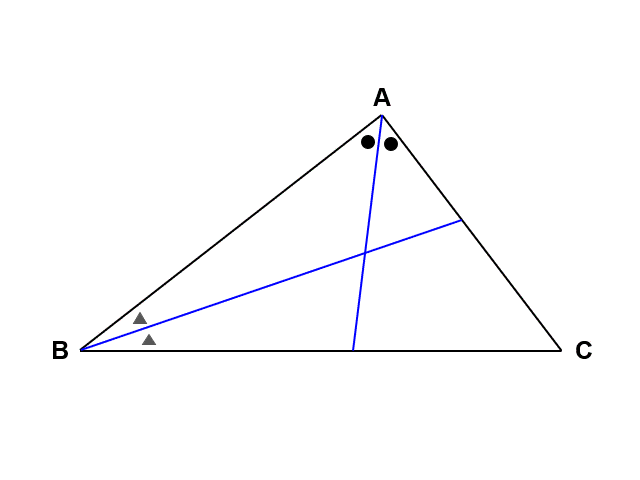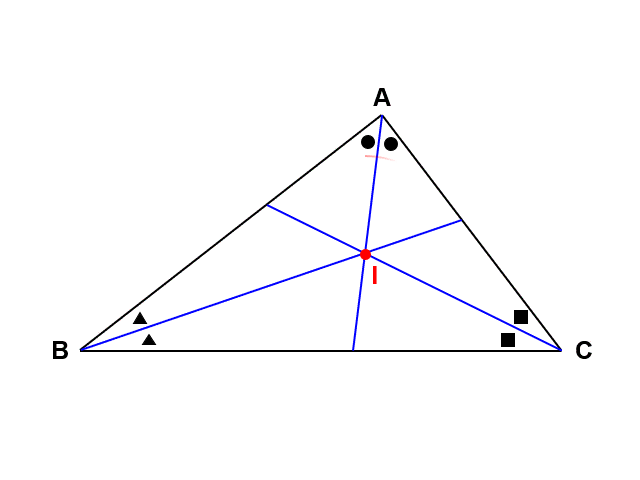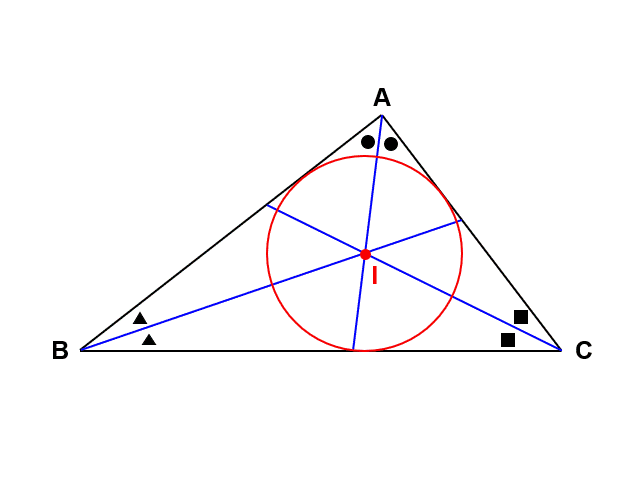
これはつまり、あらゆる三角形において内接円を作ることができるということです。三角形と円がまったく異なる図形なだけに、このようにつながるのは非常に面白いですね。
（例）
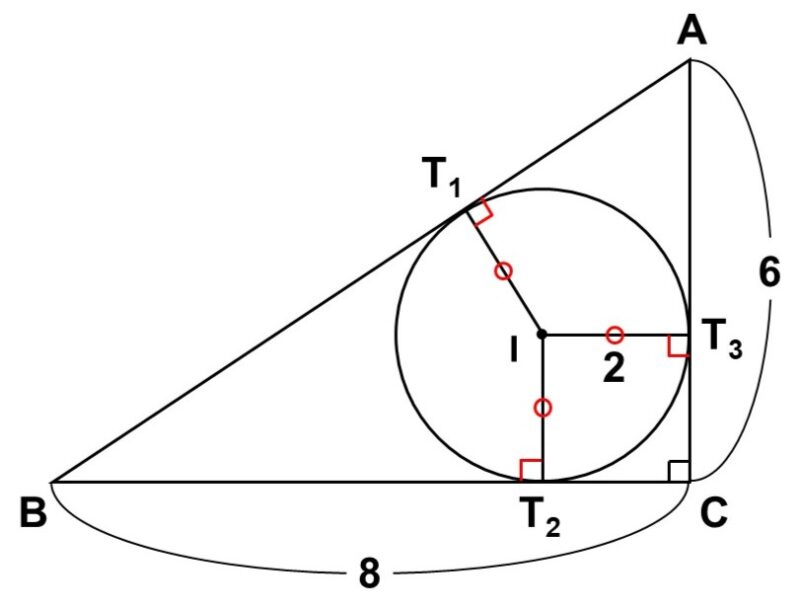
$\mathrm{BC} = 8$, $\mathrm{CA} = 6$, $\angle \mathrm{C} = 90^{\circ}$の直角三角形において、半径2の円$\mathrm{I}$が内接している。
この時、$\mathrm{AB}$の長さを求めてみよう。
四角形$\mathrm{IT_{2}CT_{3}}$に注目すると、
$\mathrm{IT_2} = \mathrm{IT_3} = 2$
$\angle \mathrm{IT_{2}C} = \angle \mathrm{IT_{3}C} = \angle \mathrm{T_{2}CT_{3}} = 90^{\circ}$
なので、この四角形は1辺の長さが2の正方形である。
また、接線の性質から、$\mathrm{AT_1} = \mathrm{AT_3}$, $\mathrm{BT_1} = \mathrm{BT_2}$なので、
$\begin{align}
\mathrm{AT_1} &= \mathrm{AT_3} \\[1.5ex]
&= \mathrm{AC}-\mathrm{T_{3}C} \\[1.5ex]
&= 6-2 = 4
\end{align}$
$\begin{align}
\mathrm{BT_1} &= \mathrm{BT_2} \\[1.5ex]
&= \mathrm{BC}-\mathrm{T_{2}C} \\[1.5ex]
&= 8-2 = 6
\end{align}$
よって、$\mathrm{AB}$の長さは
$\begin{align}
\mathrm{AB} &= \mathrm{AT_1}+\mathrm{BT_1} \\[1.5ex]
&= 4+6 =10
\end{align}$
傍心
内心は、三角形の「内角」に対して二等分線を引くことで作ることができます。その一方、三角形の「外角」に対して二等分線を引くことによっても、三角形に接するような円の中心を作ることができます。
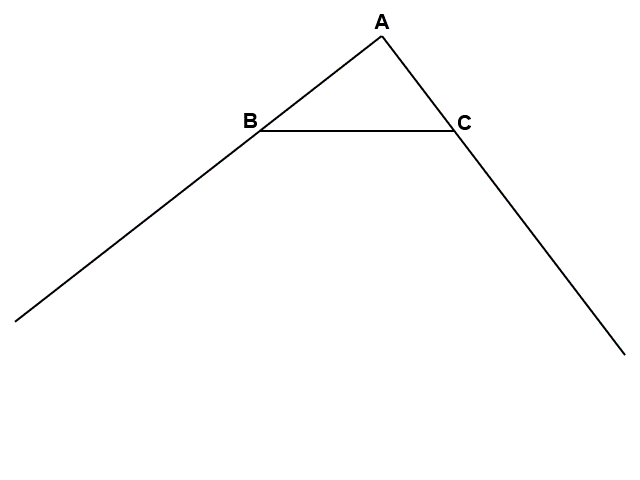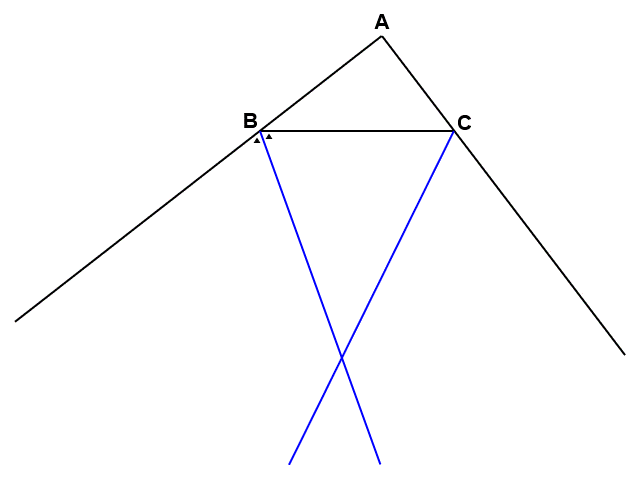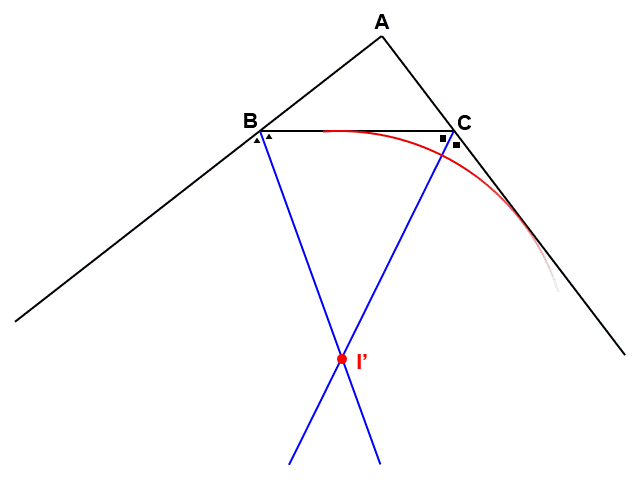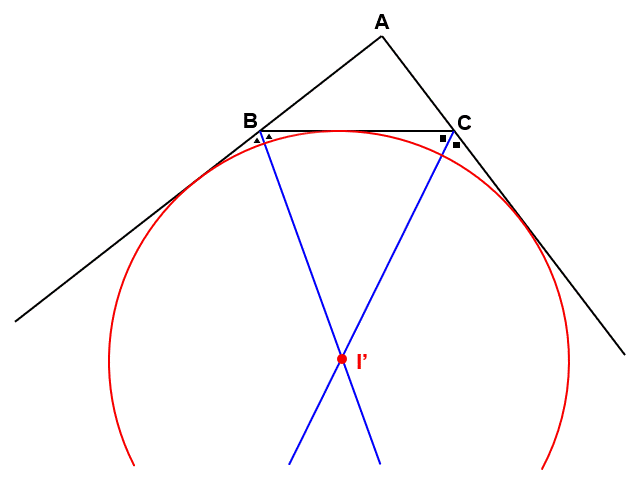
このような円は三角形の傍（そば）にできるので、傍接円（ぼうせつえん）といい、外角の二等分線が作るその中心を傍心（ぼうしん）といいます。
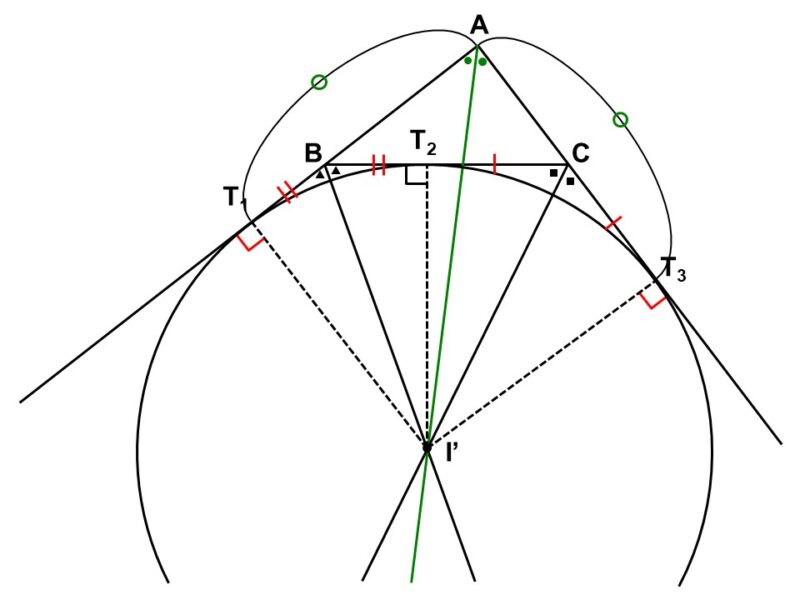
内心の時と同じように、傍心においても合同な三角形の組を見つけることができます。また、合同を利用することで、$\angle \mathrm{A}$の二等分線がちょうど傍心$\mathrm{I’}$を通ることも確かめられます（ヒントは緑の部分）。
まとめ
今回は、「円の外側」にあらわれる図形の性質について学びました。要点をまとめると次のとおりです。
- 円の中心$\mathrm{O}$と直線$l$の距離が半径$r$に等しい時、円$\mathrm{O}$と直線$l$はただ一つの共有点$\mathrm{T}$を持つ。これを「接する」といい、$l \perp \mathrm{OT}$が成り立つ。
- 円の外にある点$\mathrm{P}$から円$\mathrm{O}$に向かっては、2本の接線$l_1$, $l_2$を引くことができる。また、点$\mathrm{P}$から接点$\mathrm{T_1}$, $\mathrm{T_2}$までの長さは等しい。
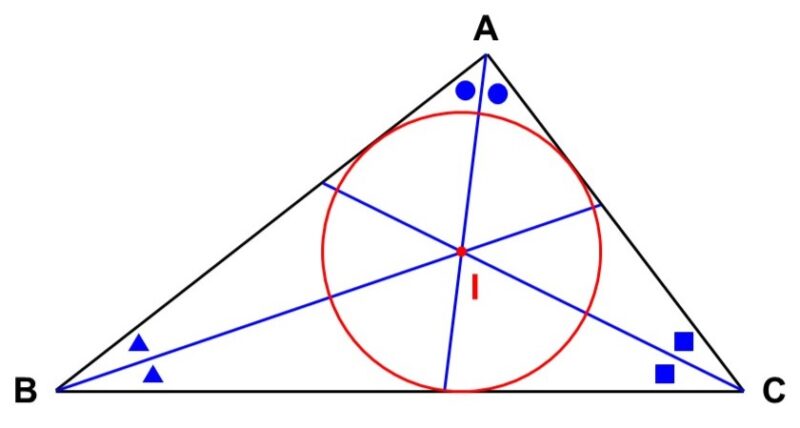
- あらゆる三角形の内角の二等分線は1点で交わり、これを中心とした内接円を描くことができる。内接円の中心を「内心」という。
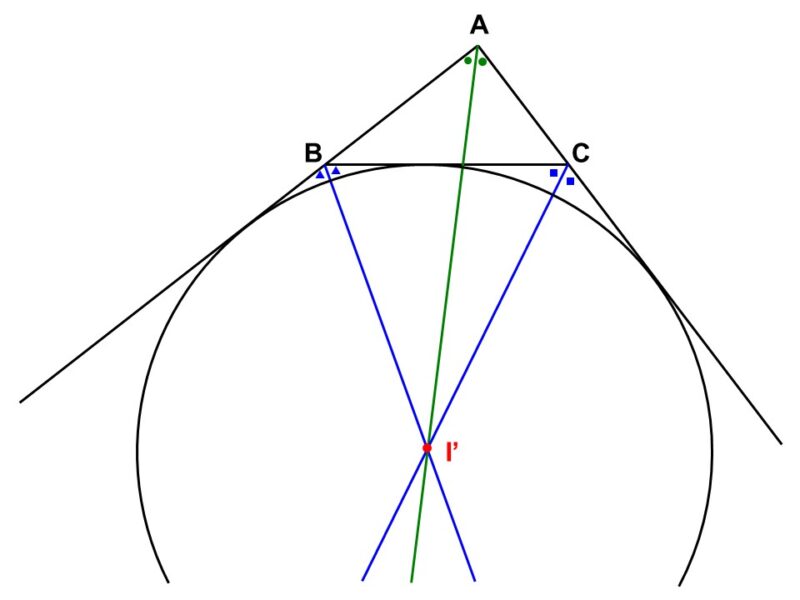
- 三角形の2頂点における外角の二等分線が作る交点を中心として、三角形にとなり合うような円（傍接円）を描くことができる。傍接円の中心を「傍心」といい、残りの頂点における内角の二等分線は傍心を通る。
三角形と円は形こそ違いますが、どちらも図形の基礎であり、ゆえに無関係ではありません。内心や傍心はその代表例だと言えますね。
次回は「円の内側」にあらわれる図形の性質について学んでいきます。こちらでもやはり三角形と円が深くつながっています…！
今回はここまでです。お疲れ様でした！
参考資料
円と接線に関する証明については、以下の動画（Youtube）を参考にさせていただきました。
[1] 円の接線が半径に垂直であることの証明 (チャンネル名：インテグレイリアン)
