こんにちは、まてがめです。
私たちは「四則演算」や「分数と小数」を通して、「数」というものを知りました。そして「場合の数と確率」を通して、人やもの、起こりうる事象を数えたり、そこから未来を予測したりすることを学びました。
つまりこれまでは「数える」という操作に注目してきたわけですが、この章では「対象物(自分が目にしているもの)について考える」ということに注目していきます。それが平面図形(へいめんずけい)と呼ばれる単元です。
この記事では、平面図形のルールとも言える5つの公理について学んでいきます。
平面図形を学ぶ意味とは?
そもそも「平面図形」という単元を学ぶ意味は、次の2つが挙げられます。
- 最終的には、私たちが普段扱う立体(3次元)について理解ができるようになる
- 論理的な思考力が身につく
1つ目はイメージしやすいでしょうか。そもそも平面図形という学問は「土地をどう分けたらよいか?」や「どうやって測量すればよいか?」といった、人間社会でよく起こる問題を解決する手段として発展してきたという歴史があります。
もちろん、現代でも建築や測量には欠かせないものですし、3DプリンターやVR・ARといった最新技術を使いこなすにも、平面図形についての理解が必要です。
2つ目はピンとこない人もいるかもしれませんが、実は平面図形という単元は「論理的思考」と深い関わりがあります。
平面図形に関する内容は、古代の数学者ユークリッド(エウクレイデス)によって初めて体系的にまとめられました。その時、彼が大切にしていたのが「論理性」でした。
すなわち、初めに前提(公理や定義)を決め、それを基にして成り立つこと(定理)を積み重ねるようにしたわけです。こうしてユークリッドは、自分の主観や思いこみから誤りが生まれることを防ぎ、論理的で間違いのないものとして平面図形の内容をまとめあげました[1]。
論理的な思考力は、文章を書いたり議論を行ったりする上で重要なスキルですが、論理性を意識して作られている「平面図形」という単元は、まさにこの力をきたえるのに適していると言えるでしょう。
平面図形におけるルール ― 公理
最初にお話ししたように、平面図形ではすべての前提となる公理(こうり)があります。これはスポーツやゲームで言うところのルールであり、これをスタート地点にしていろいろな図形の性質(定理)を導いていきます[1]。
ルールとなる公理は次の5つしかありません。
- 異なる2点に対して、これらを通る直線を引くことができる
- 直線の両端は限りなく伸ばすことができる
- すべての直角は互いに等しい
- 任意の中心と半径に対して円を描くことができる
- ある直線$l$に対して、直線$l$上にない点を通り、かつ直線$l$と交わらない直線は1本のみ引ける
前提となる事柄なので、当たり前のように感じるものが多いですが、一つずつ中身を見ていきましょう。
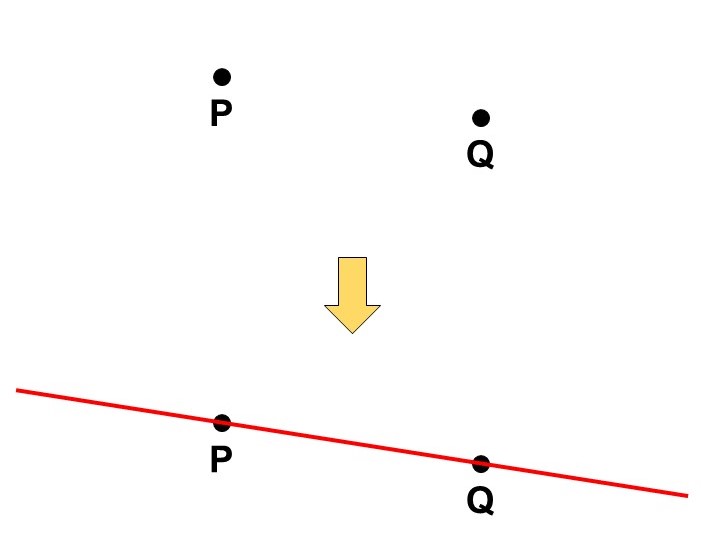
1. 異なる2点に対して、これらを通る直線を引くことができる
点とは「大きさ(面積)を持たない図形」のことを指します。点は英語でPointなので、記号でP, Q, R…と名付けられることが多いです。
1つ目の公理が言っているのは、「2点$\mathrm{P}$, $\mathrm{Q}$がある時に、$\mathrm{P}$, $\mathrm{Q}$を通る直線が引ける」ということです。そのままですね。なお、このような直線は1本しか引くことができません。
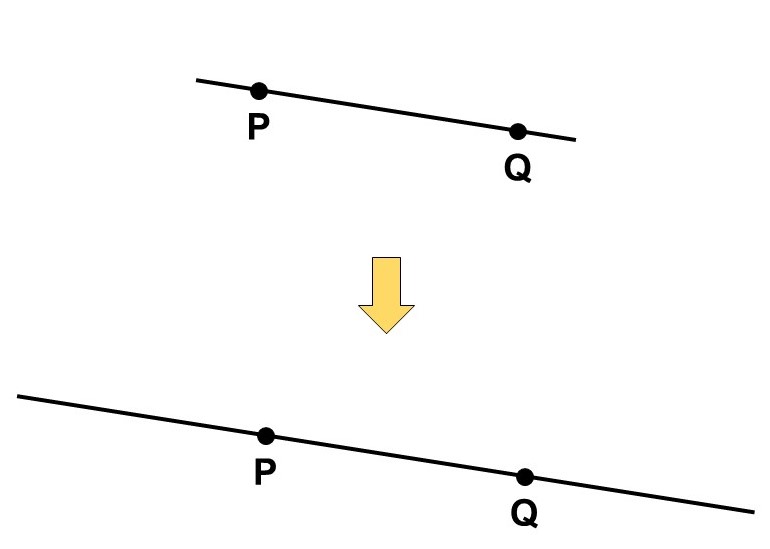
2. 直線の両端は限りなく伸ばすことができる
2つ目の公理についても言葉通りです。図形について考える時は、必要に応じて直線はいくらでも長くすることができます。例えば「与えられた直線は5 cmで描いてあるから、これで考えないといけない」なんてことはないということですね。
ちなみに、平面図形で出てくる「線」は次の3種類があります。この機会に覚えてしまいましょう。
- 線分(せんぶん):両端が決まっている線

- 半直線(はんちょくせん):片端が決まっていて、もう片端が無限に続く線

- 直線(ちょくせん):両端が無限に続く線

3. すべての直角は互いに等しい
この公理を理解するために、先に角度(かくど)について簡単に説明しておきましょう。
例えば、2つの直線$l$, $m$が交わっているとします(直線は英語でlineなので、$l$, $m$, …と記号をふります)。この時、「2つの直線がどのくらい開いているか」を角度といい、図のように左側と右側で2種類考えることができます。
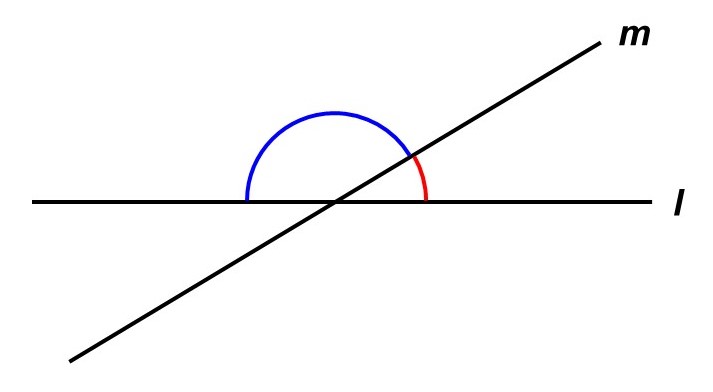
特に、左側の角度と右側の角度が等しい時、直線$l$, $m$は垂直(すいちょく)であるといい、$l \perp m$と表します。また、この時の角度を直角(ちょっかく)といいます。
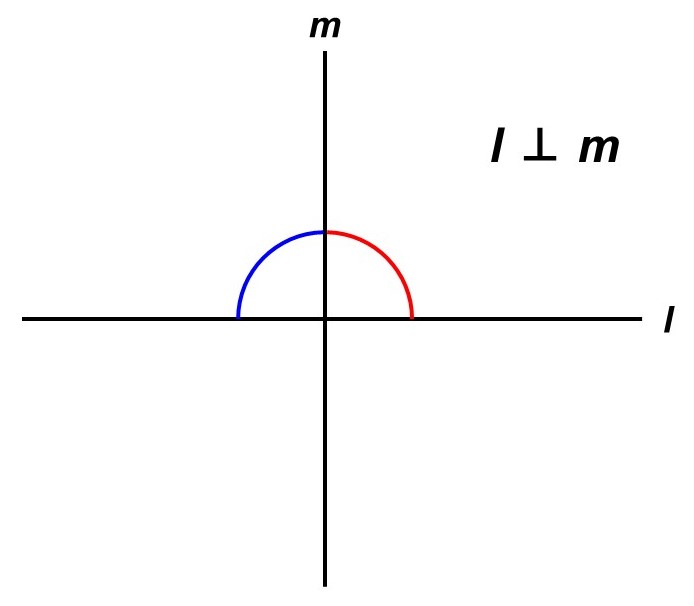
3つ目の公理が言っているのは、この「直角」がどんな作られ方であっても角度としてはすべて等しいということです。直角の意味がわかれば、そこまで不思議ではないですね。
4. 任意の中心と半径に対して円を描くことができる
まず円の定義ですが、これは「中心となる点から等しい距離にある点が集まってできた図形」を表します。コンパスで円を描いたことがあればわかりますね。
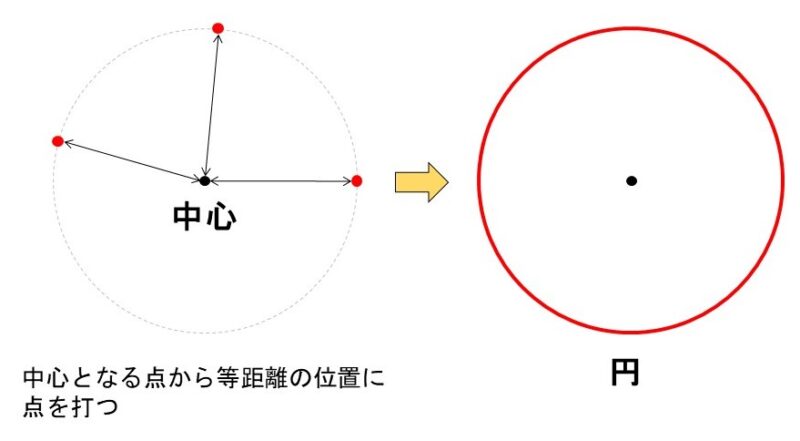
任意(にんい)という言葉は数学においてよく出てくる言葉で、「好きなように、自由に」という意味です。すなわち4つ目の公理が言っているのは、「中心となる点とそこからの距離を自由に決めて円を描くことができる」ということです。
コンパスの大きさには限りがありますが、2つ目の公理における直線と同じく、頭で考える分には円の大きさは自由です。
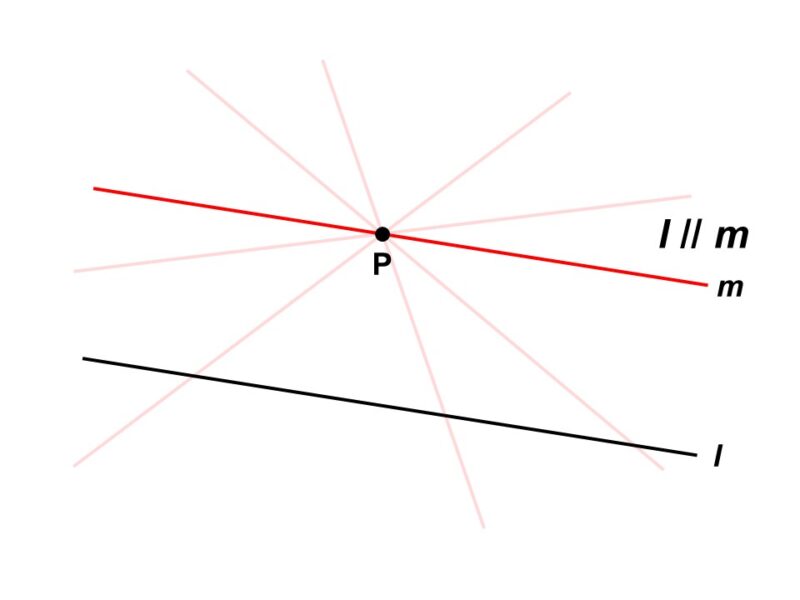
5. ある直線$l$に対して、直線$l$上にない点を通り、かつ直線$l$と交わらない直線は1本のみ引ける
この公理は今までの4つと比べると、言葉だけでは少しピンとこないかもしれませんが、図を描いてみるとよく理解できます。まず、適当な直線$l$と直線$l$上でない場所に点$\mathrm{P}$を用意します。
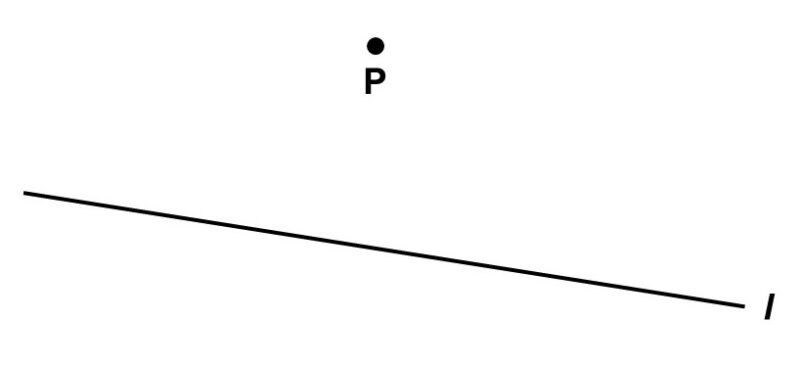
さて、点$\mathrm{P}$を通って直線$l$と交わらないような直線$m$はいくつあるでしょうか?いろいろな直線を描いてみれば気がつきますが、そのような直線は1本しか引けません。それ以外だと、必ずどこかで$l$と交わってしまいます。
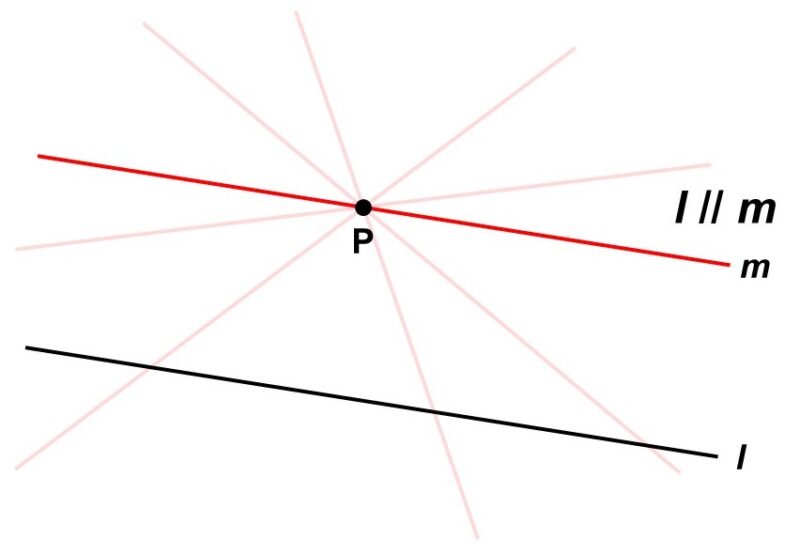
5つ目の公理が言っているのは、まさにこのことです。直線$l$, $m$が交わらない時、直線$l$, $m$は平行(へいこう)であるといい、$l / \! / m$と表します。
まとめ
今回は平面図形を学ぶ準備として、前提となる5つの公理を学びました。
これから学んでいく図形の性質(定理)には、一目見ただけでは思いつかないようなものもありますが、すべてこの公理が出発点になっています。公理から定理が、定理から別の定理が導かれていく様を楽しみながら学んでいきましょう!
今回はここまでです。お疲れさまでした!
参考資料
[1] ビジュアルガイド もっと知りたい数学 深遠なる「幾何学」の世界 (マイク・ゴールドスミス(訳:緑慎也) / 創元社 2021)