こんにちは、まてがめです。
この階では、これまで学んできた場合の数と確率についての内容を総復習していきます。細かく見れば内容の多かった章ですが、次の大きな流れがわかっていれば大丈夫です。
- 場合の数を数える時の基本は「樹形図」
- 場合の数の中でもシンプルで計算しやすく、もっとも応用しやすいのが「順列」
- 順列をベースにすると、いろんな場面で登場する「組合せ」を数えることができる
- 必要に応じて「集合(ベン図)」を活用すると、複雑な場合の数も数えやすくなる
- 場合の数から「確率」、確率から「期待値」を考えることで、未来を予測できる
逆にこれがわかっていると、細かい部分の理解もしやすくなります。なので、これを意識しながら復習していきましょう。
場合の数
場合の数とは、「起こりうる場合(事象)の数」です。場合の数をもれなく数えることは、物事を正しく理解するのに欠かせません。そのため、この章に限らず、数学(理学)における大切な操作だと言えます。
場合の数を正しく数えるための方法は大きく分けて4つあります。それが「樹形図・順列・組合せ・集合」です。状況に応じてこれらを使い分けたり、あるいは組み合わせたりして、場合の数を数えていくことになります。
樹形図
場合の数を数える上で、一番基礎的な方法が「樹形図」です。その名前の通り、起こりうる場合を木の枝のような図にすることで場合の数を数えます。
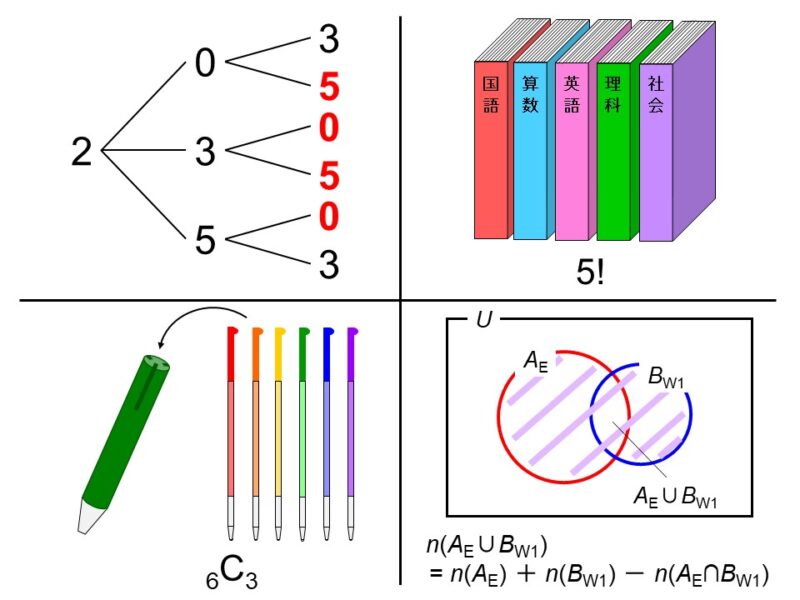
(例1)
0, 2, 3, 5の4つの数字のうち、3つの数字を使って3桁の数を作る。この時、5の倍数となる数の作り方は、樹形図から10通り。
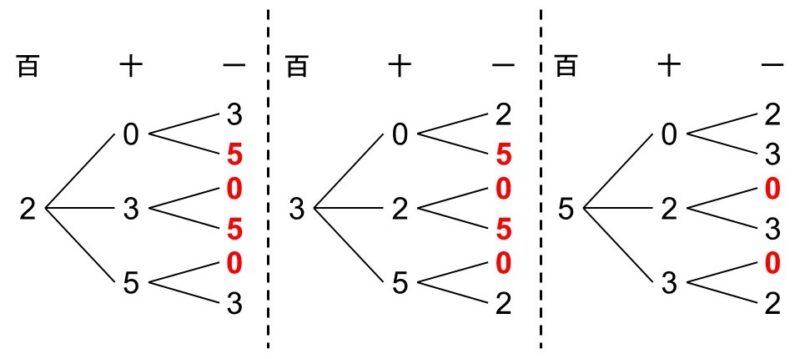
樹形図はあらゆる場面において使える方法なので、考えられる場合の数が少ない時や場合の数をうまく数える方法が思いつかない時には、まず試したい方法です。
ただし、場合の数が多くなってくると図を描くのも難しくなります。したがってその際は、他の3つの方法も使う必要があります。
詳しい解説はこちら↓
順列
「順列」とは「人やものを順番に並べた列」のことです。順列における場合の数は、次の例のように掛け算で簡単に求めることができます。
(例2)
ここに国語、算数、英語、理科、社会の5冊の教科書がある。

これらの教科書すべてを本棚に並べる場合、その並べ方は
$5! = 5 \times 4 \times 3 \times 2 \times 1 = 120$
すなわち、120通り。
しかし、教科書はそれぞれがかなりの厚さだったため、3冊のみ本棚にしまうことにした。この場合、その並べ方は
${}_5 \mathrm{P}_3 = 5 \times 4 \times 3 = 60$
すなわち、60通り。
(例3)
Aさんは友人のBさんから、旅行のおみあげとしてチョコをもらった。箱にはプレーン味、いちご味、抹茶味の3種類の味がそれぞれ2個ずつ入っている。

Aさんは、最後の1個がいちご味のチョコになるように食べていくことにした。この場合、食べ方のパターンは
$\begin{align}
& \hspace{13pt} \dfrac{5!}{2! \times 2!} \\[1.5ex]
& = \dfrac{5 \times 4 \times 3 \times 2 \times 1}{(2 \times 1) \times (2 \times 1)} \\[1.5ex]
& = 30
\end{align}$
すなわち、30通り。
順列の良いところは、一見するとものや人の並び順を考えていないような状況でも、順列の問題に置きかえることで、簡単に答えが求まる点です。積極的に使っていきたい方法の1つですね。
詳しい解説はこちら↓
組合せ
「組合せ」はいろんな場面で登場するので、一番よく使う方法かもしれません。
順列との大きな違いは「並び順を考えなくてよい」という点です。しかし裏を返せば、順列として考えた後、並び順の区別をなくすことで場合の数を数えることができます。
(例4)
Aさんは自分で色をカスタマイズできるボールペンを買ってきた。芯の取り付け枠は3つあり、Aさんは今回、6種類の色をそれぞれ1本ずつ用意した。
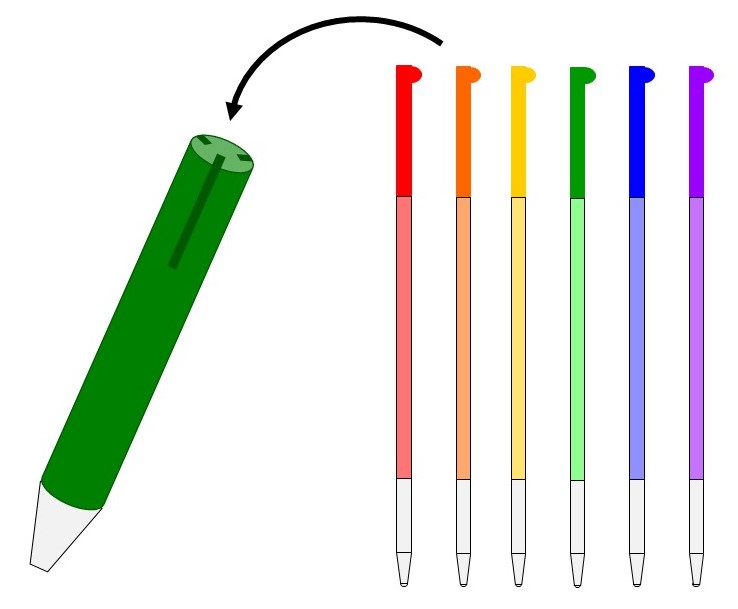
芯の取り付け枠をすべて使うものとすると、カスタマイズの方法は
$\begin{align}
{}_6 \mathrm{C}_3 & = \dfrac{{}_6 \mathrm{P}_3}{3!} \\[1.5ex]
& = \dfrac{6 \times 5 \times 4}{3 \times 2 \times 1} \\[1.5ex]
& = 20
\end{align}$
すなわち、20通り。
詳しい解説はこちら↓
集合(ベン図)
「集合」とは、それぞれの場合(事象)ごとに1つの「集まり」とみなし、その集まり同士の関係を考える方法です。基本的にはベン図と呼ばれる図を用いて考えます。
(例5)
Aさんの学校では今日、文化祭が行われている。Aさんは自分のクラスの出し物を宣伝しようと、同じクラスのBさん、Cさん、Dさん、Eさん、Fさんと協力して学校中を回ることにした。校舎は3階建てで、東校舎と西校舎に分かれているため、東西で二手に分かれ、1人1フロアを担当するとする。
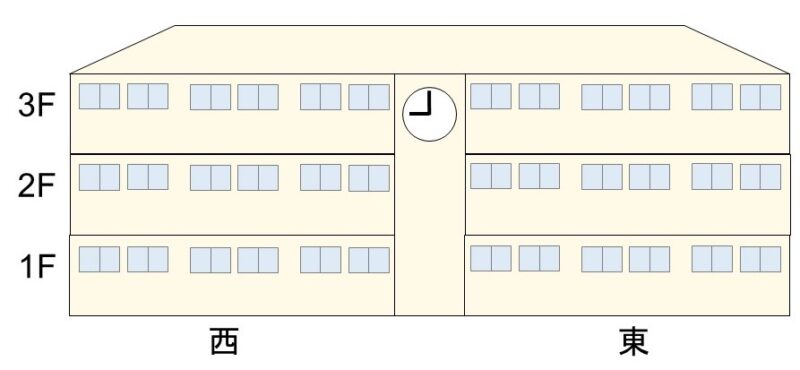
この時、「Aさんが東校舎を担当する」または「Bさんが西校舎の1階を担当する」場合の数を計算してみよう。東校舎を担当する場合を$A_{\mathrm{E}}$、西校舎の1階を担当する場合を$B_{\mathrm{W1}}$とすると、次のようなベン図が描ける。
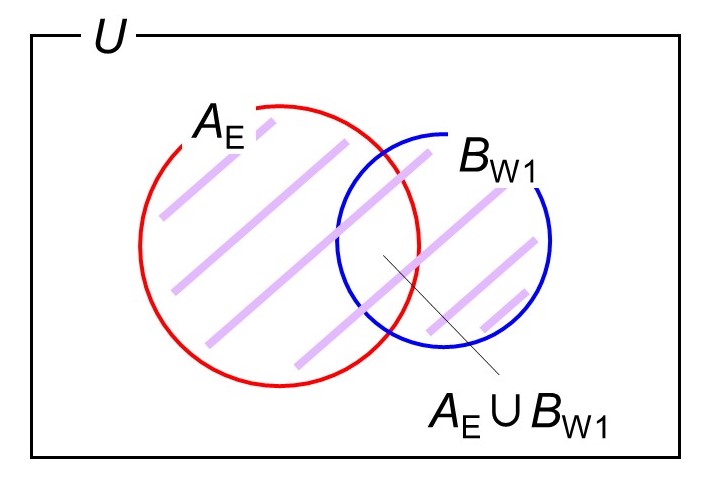
Aさんが東校舎を担当する場合、残り5人から東校舎の担当2人を選び(選ばれなかった3人が自動的に西校舎)、各校舎で割りふりを決めればよいので、
$n(A_{\mathrm{E}}) = {}_5 \mathrm{C}_2 \times 3! \times 3! = 360$
Bさんが西校舎の1階を担当する場合、残り5人については順番に担当を決めればよいので、
$n(B_{\mathrm{W1}}) = 5! = 120$
Aさんが東校舎を担当し、かつBさんが西校舎の1階を担当する場合、残り4人から東校舎の担当2人を選び(選ばれなかった2人が自動的に西校舎)、各校舎で割りふりを決めればよいので、
$n(A_{\mathrm{E}} \cap B_{\mathrm{W1}}) = {}_4 \mathrm{C}_2 \times 3! \times 2! = 72$
以上より、求める場合の数$n(A_{\mathrm{E}} \cup B_{\mathrm{W1}})$は、
$\begin{align}
n(A_{\mathrm{E}} \cup B_{\mathrm{W1}}) & = n(A_{\mathrm{E}})+n(B_{\mathrm{W1}})-n(A_{\mathrm{E}} \cap B_{\mathrm{W1}}) \\[1.5ex]
& = 360+120-72 \\[1.5ex]
& = 408
\end{align}$
(例7に続く)
複雑な場合の数を数える時には集合(ベン図)の考え方を使う必要があります。また、確率を考える際にも大きなよりどころになります。
詳しい解説はこちら↓
確率
確率とは?
「コインを投げる」や「サイコロを振る」のように、「同じ操作として何回でもくり返すことができ、得られる結果は偶然である」ような操作を試行といいます。このような試行に対し、割合を表す量として「確率」を考えることができます。
$\dfrac{\text{ある場合の数}}{\text{起こりうるすべての場合の数}}$
言いかえれば、確率は「ある事象が、起こりうるすべての事象のうち、どのくらいの割合を占めているか」を表しています。したがって、求めた確率が大きければ、その事象が起こる可能性も大きいと考えることができます。
(例6)
今からAさん、Bさん、Cさんの3人でジャンケンを行う。この時、1回で勝負が決まらない(あいこになる)確率を計算してみよう。
起こりうる場合の数は、3人おのおのでグー・チョキ・パーの3通りの出し方があるので、
$3 \times 3 \times 3 = 27$通り
一方、あいこになる場合の数は、
- 3人全員が同じ手を出す場合 … 3通り
- 全員が相異なる手を出す場合 … $3! = 6$通り
の合わせて9通り。
よって、その確率は
$\dfrac{9}{27} = \dfrac{1}{3}$
1つ注意したいのが、確率を計算する時に考えるすべての事象は、同様に確からしい(等しく起こる可能性がある)ものでなければならないという点です。
例えば、くじで1等が当たる確率を考えるとします。この時、「起こりうる場合の数は【当たる】と【当たらない】の2通りだから、その確率は$\frac{1}{2}$」とはなりません。
これは、【当たる】という事象と【当たらない】という事象が同様に確からしくないからです。実際には、1等のくじの数に対してそれ以外のくじがたくさんあるわけですから、引き当てうるくじの一つ一つ(=同様に確からしい事象)を考えて初めて正しく確率が計算できることになります。
詳しい解説はこちら↓
確率の特性
確率においては、状況次第で四則演算(足し算・引き算・掛け算・割り算)を行うことができます。
確率の足し算・引き算(ベン図の利用)
確率では、同じ試行について考えている限り、その分母となる「起こりうる場合の数」は変わりません。したがって、場合の数と同じように、確率でも集合(ベン図)を用いた計算(足し算・引き算)を行うことができます。特に、ある2つの事象が同時に起こらない場合を排反といい、2つのどちらかが起こる確率(和事象の確率)については、足し算だけで計算できます。
(例7)
例5において、校舎の分担をくじ引きで決めることにした。この時、Aさんが東校舎または西校舎の1階を担当する確率$P(A_{\mathrm{E}} \cup A_{\mathrm{W1}})$を計算してみよう。
「東校舎」に対応するくじは、6本中3本あるので、
$P(A_{\mathrm{E}}) = \dfrac{1}{2}$
「西校舎の1階」に対応するくじは、6本中1本あるので、
$P(A_{\mathrm{W1}}) = \dfrac{1}{6}$
事象$A_{E}$、$A_{W1}$は排反なので、求める確率は
$\begin{align}
P(A_{\mathrm{E}} \cup A_{\mathrm{W1}}) & = P(A_{\mathrm{E}})+P(A_{\mathrm{W1}}) \\[1.5ex]
& = \dfrac{1}{2}+\dfrac{1}{6} \\[1.5ex]
& = \dfrac{2}{3}
\end{align}$
確率の掛け算(独立)
例えば、コインを投げるという試行をくり返し行うとします。この時、表裏のどちらが出るかというのは、前の結果には左右されませんし、後の結果に影響することもありません。このような場合、それぞれの試行は独立であるといいます。
互いに独立な試行について確率を考える場合、その確率は掛け算で計算することができます。
(例8)
コインを4回投げ、その表裏を確認する。
この時、表が2回、裏が2回出る確率を計算してみよう。
1回の試行において表が出る確率、裏が出る確率はともに
$\dfrac{1}{2}$
また、試行は互いに独立なので、表裏が出る順番にかかわらずその確率は
$(\dfrac{1}{2})^2 \times (\dfrac{1}{2})^2 = \dfrac{1}{16}$
一方、表裏の出方は、1~4回目のうちどの2回で表が出るかを考えればよいので、
${}_4 \mathrm{C}_2 = \dfrac{4 \times 3}{2 \times 1} = 6$
これら6通りの事象は互いに排反なので、求める確率は
$6 \times \dfrac{1}{16} = \dfrac{3}{8}$
(例10に続く)
確率の割り算(条件付き確率)
確率を考える時、その確率にかかわるような情報があらかじめわかっている場合があります。このような状況下で求める確率を条件付き確率といい、確率の割り算で計算できます。
(例9)
とあるお店では、景品がもらえるくじ引きキャンペーンを2日間限定で開催している。くじは全部で20本あり、その中に1等は2本だけ入っている。Aさんが2日目にお店に立ち寄ったところ、残りのくじの本数は5本となっていた。
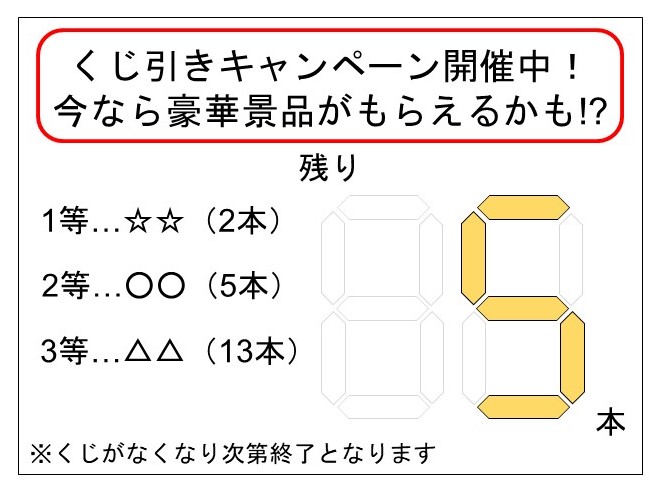
ここで、Aさんがくじ引きに挑戦して1等を引き当てる確率を計算してみよう。
5本のくじの中に1等のくじが残るという事象を$I$、Aさんが1等を引き当てるという事象を$A$とすると、求める条件付き確率は
$P_{I}(A) = \dfrac{P(I \cap A)}{P(I)}$
5本のくじの中に1等のくじが残らない場合(余事象$I^c$)に着目してみると、これはその前に引いた15本のくじに1等のくじがすべて含まれる場合なので、
$\begin{align}
P(I^c) & = \dfrac{{}_2 \mathrm{C}_2 \times {}_{18} \mathrm{C}_{13}}{{}_{20} \mathrm{C}_{15}} \\[1.5ex]
& = \dfrac{{}_{18} \mathrm{C}_5}{{}_{20} \mathrm{C}_5} \\[1.5ex]
& = \dfrac{15 \times 14}{20 \times 19} \\[1.5ex]
& = \dfrac{21}{38}
\end{align}$
よって、確率$P(I)$は
$\begin{align}
P(I) & = 1-P(I^c) \\[1.5ex]
& = 1-\dfrac{21}{38} \\[1.5ex]
& = \dfrac{17}{38}
\end{align}$
Aさんが1等を引き当てる場合は、[1] 5本のくじの中に1等のくじが2本残っており、そのどちらかを引き当てる、[2] 5本のくじの中に1等のくじが1本残っており、それを引き当てる、の2通り。それぞれの場合における確率を計算すると、
[1] 5本のくじの中に1等のくじが2本残っており、そのどちらかを引き当てる場合
$\begin{align}
& \hspace{13pt} \dfrac{{}_{18} \mathrm{C}_{15}}{{}_{20} \mathrm{C}_{15}} \times \dfrac{{}_2 \mathrm{C}_1}{{}_5 \mathrm{C}_1} \\[1.5ex]
& = \dfrac{1}{19} \times \dfrac{2}{5} \\[1.5ex]
& = \dfrac{2}{95}
\end{align}$
[2] 5本のくじの中に1等のくじが1本残っており、それを引き当てる場合
$\begin{align}
& \hspace{13pt} \dfrac{{}_2 \mathrm{C}_1 \times {}_{18} \mathrm{C}_{14}}{{}_{20} \mathrm{C}_{15}} \times \dfrac{{}_1 \mathrm{C}_1}{{}_5 \mathrm{C}_1} \\[1.5ex]
& = \dfrac{15}{38} \times \dfrac{1}{5} \\[1.5ex]
& = \dfrac{3}{38}
\end{align}$
[1]と[2]は排反なので、確率$P(I \cap A)$は
$P(I \cap A) = \dfrac{2}{95}+\dfrac{3}{38} = \dfrac{1}{10}$
以上より、求める確率P_{I}(A)は
$\begin{align}
P_{I}(A) & = \dfrac{P(I \cap A)}{P(I)} \\[1.5ex]
& = \dfrac{\dfrac{1}{10}}{\dfrac{17}{38}} \\[1.5ex]
& = \dfrac{19}{85}
\end{align}$
詳しい解説はこちら↓
確率の特性については、次の練習問題を解くことでも理解を深めることができます。ぜひチャレンジしてみてください!
期待値
確率を考える場面では、試行の結果として、得点や金額のように何かしらの「値」が決まるようなことが多くあります。このような場面では、値とその値が出る確率を掛け合わせることで、「どのくらいの値になることが期待できそうか」を表す量として「期待値」を考えることができます。
(例10)
例8の試行(コイントス)を使って「表 → 10点 / 裏 → 0点」となるゲームを行う。この場合、得点と確率の関係は次の表のようになる。
| 表が出た回数 | 0 | 1 | 2 | 3 | 4 |
| 得点 | 0 | 10 | 20 | 30 | 40 |
| 確率 | $\dfrac{1}{16}$ | $\dfrac{4}{16}$ | $\dfrac{6}{16}$ | $\dfrac{4}{16}$ | $\dfrac{1}{16}$ |
よって、このゲームにおける得点の期待値は
$\begin{align}
& \hspace{13pt} 0 \times \dfrac{1}{16}+10 \times \dfrac{4}{16}+20 \times \dfrac{6}{16}+30 \times \dfrac{4}{16}+40 \times \dfrac{1}{16} \\[1.5ex]
& = \dfrac{0 \times 1+10 \times 4+20 \times 6+30 \times 4+40 \times 1}{16} \\[1.5ex]
& = \dfrac{320}{16} = 20
\end{align}$
ちなみに期待値は、計算の上では平均と同じものです。
詳しい解説はこちら↓
まとめ
場合の数と確率の理解に必要なものは、基本的に四則演算と分数・小数だけです。
ですが、ここで学ぶ「ものの数え方」や「確率・期待値の考え方」は、理学に欠かせないのはもちろんのこと、日常生活や経済にも広く応用されています。つまり、身近な物事にも学術的な問題にも使える方法だと言えます。
ぜひともこの章の考え方を身につけて、学問や生活に役立てていきましょう!
今回はここまでです。また次の階でお会いしましょう!