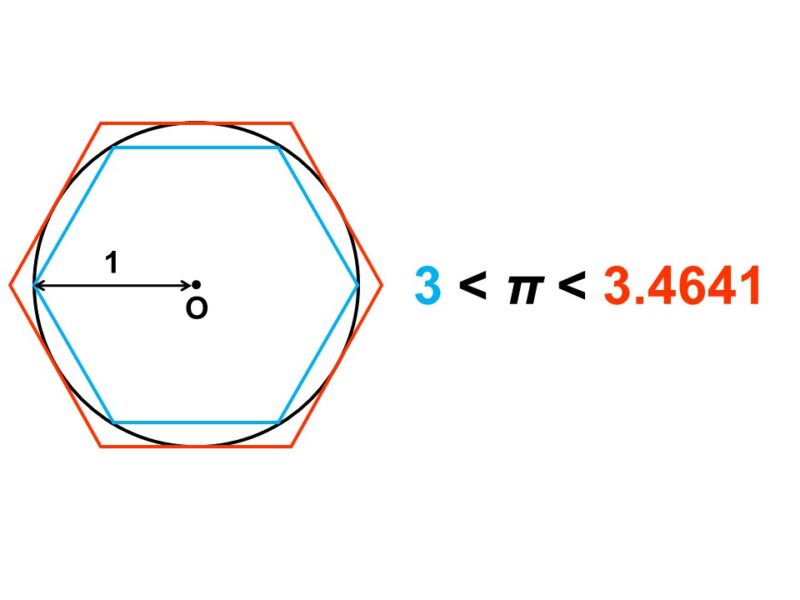こんにちは、まてがめです。
前回までに、平面図形の主役である「三角形」について、その性質や形・大きさに注目しながら学んできました。
- 30F 「三角形が持つ性質とは?」 ― 三角形の内角の和・辺と角の関係・成立条件
- 31F 「同じ三角形を作るための条件とは?」 ― 三角形の合同
- 32F 「小さな三角形からピラミッドの大きさもわかる!?」 ― 相似と三角比
- 33F 「図形の大きさを表す指標」 ― 面積
今回からは、平面図形におけるもう一人の主役「円」について学んでいきます。円はシンプルな図形ですが、とても奥が深く、学ぶ要素の多い図形でもあります。
円の定義
実は、円について話すのはこれが初めてではありません。この章の最初の「平面図形における5つの公理」の中で円が出てきています。
「任意の中心と半径で円を描くことができる」
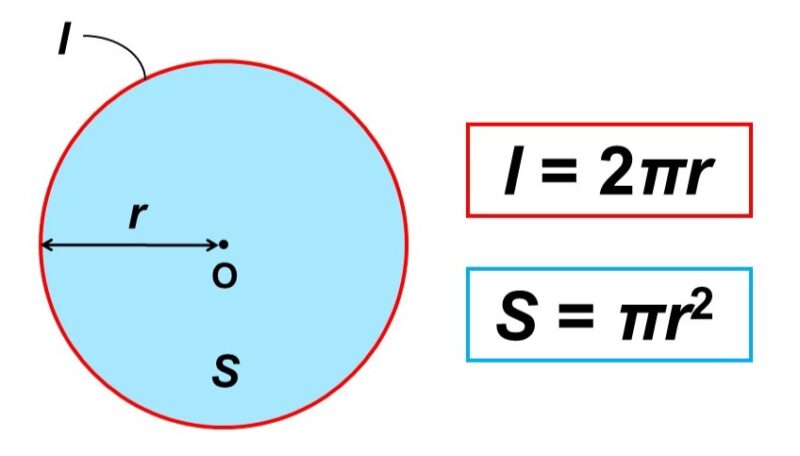
復習ですが、円とは「(中心となる)ある点から一定の距離にある点が集まってできる」図形のことを表します。この時、中心$\mathrm{O}$からの距離を半径(半径を意味するradiusの頭文字$r$で表します)と呼び、円の端から端までの長さ(半径の2倍)を直径と呼びます。
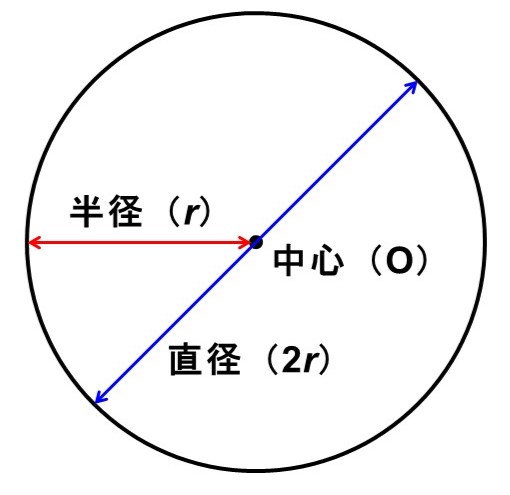
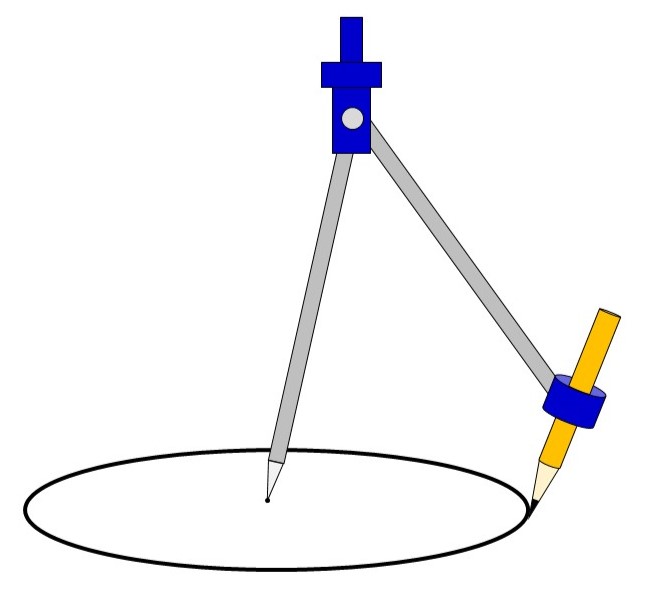
この定義にしたがって円を描くための道具が「コンパス」です。針の部分で中心となる点を決め、針から鉛筆までの距離(半径)を決めることで、好きな大きさの円を描くことができます。
円の対称性
円が他の図形と大きく異なるのが、その対称性(たいしょうせい)です[1]。
対称性とは、図形に対して対称操作(鏡映・回転)を行った時、その前後で図形が変わらないか(=元の図形と重ねられるか)を表すものです。
いくつかの図形を例に、対称性の考え方を理解してみましょう。
二等辺三角形の場合
1つ目の例は二等辺三角形です。この図形は、鏡映(鏡写しにする操作)を行う前後で変わりません。
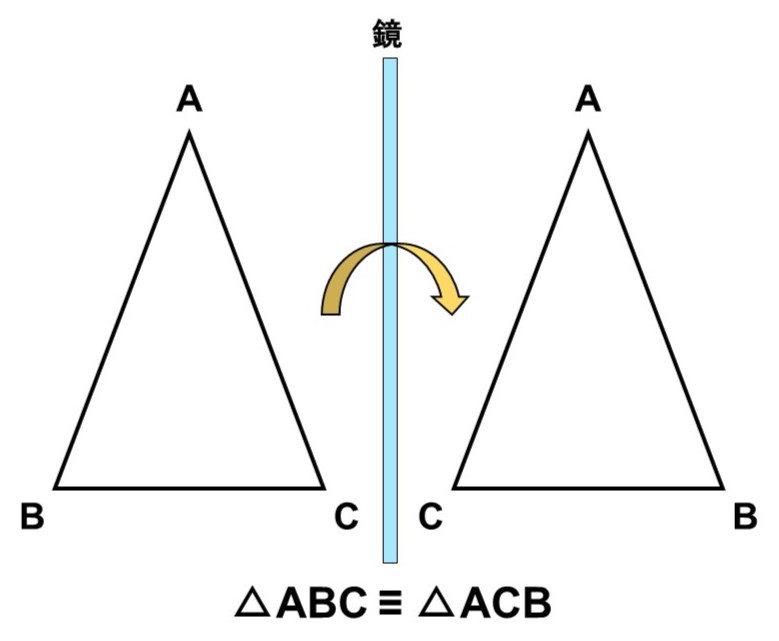
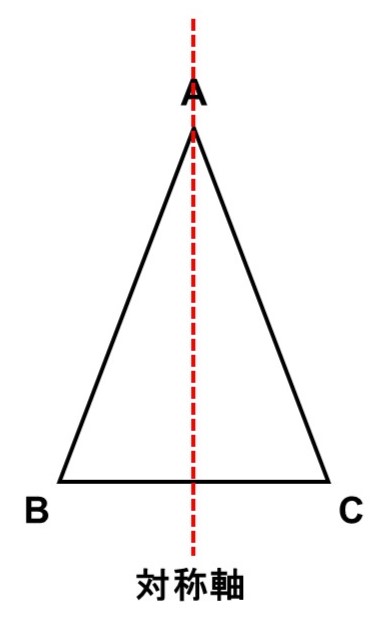
このような図形を線対称(せんたいしょう)といい、その対称性を生み出している対称軸(たいしょうじく)を持っています。二等辺三角形の場合は、対称軸を1本持っています。
平行四辺形の場合
2つ目の例は平行四辺形です。この図形は、180°回転させる前後で変わりません。
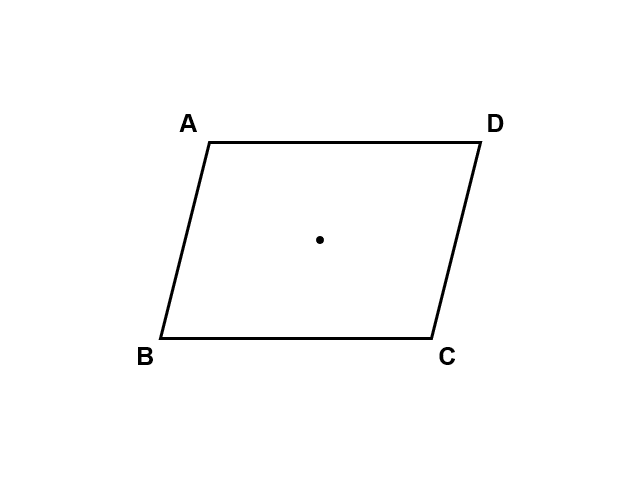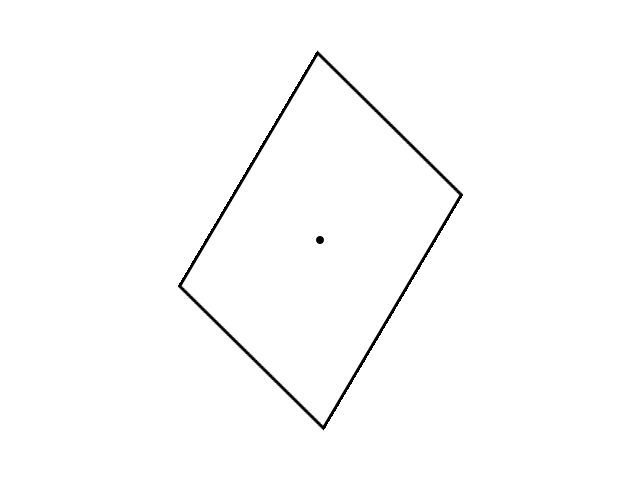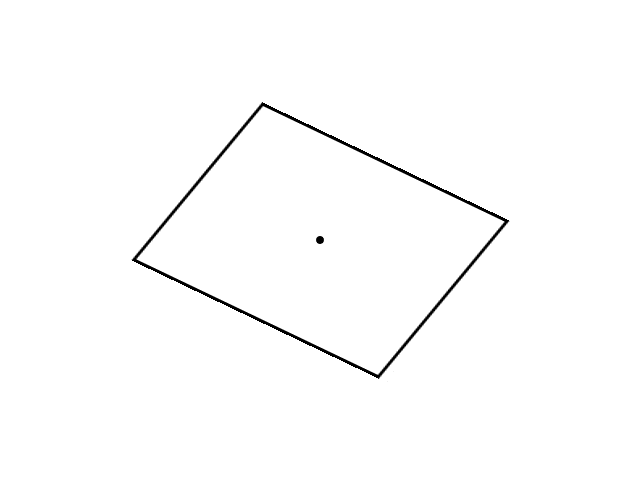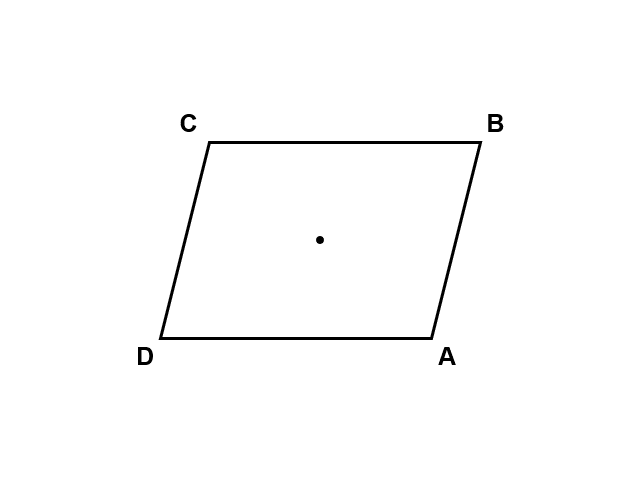
このような図形を点対称(てんたいしょう)といいます。ただし、どんな図形も1回転(360°)させれば元の図形と重なってしまうので、点対称な図形に分類するのは180°以下の回転によって元の図形と重なる場合が普通です。
正方形の場合
3つ目の例は正方形です。この図形には、元の正方形と重なる鏡映のパターンが4つあり、加えて180°回転または90°回転で元の図形と重ねることができるため、線対称かつ点対称な図形です。
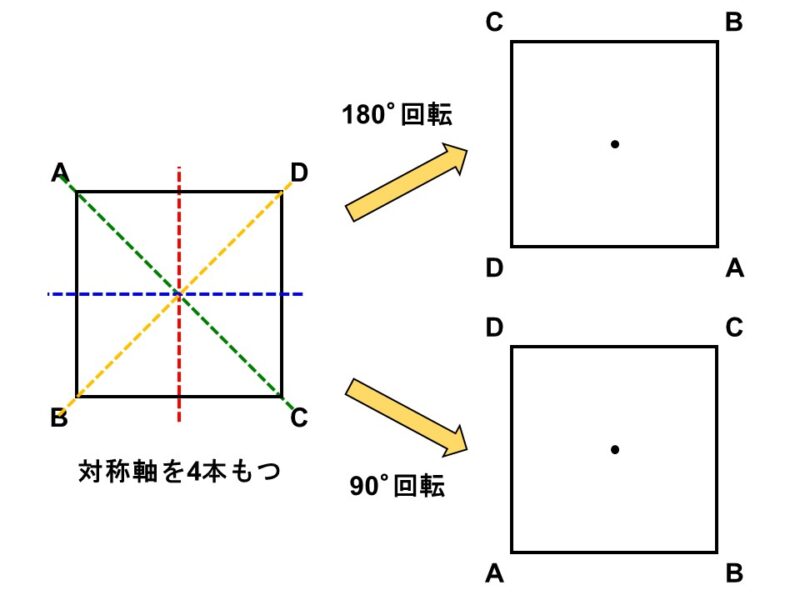
対称操作のパターンが多ければ多いほど、その図形は「対称性が高い」図形ということになります。つまり、正方形は二等辺三角形や平行四辺形よりも対称性が高い図形です。
円の場合
以上をふまえて、円の対称性について考えてみます。
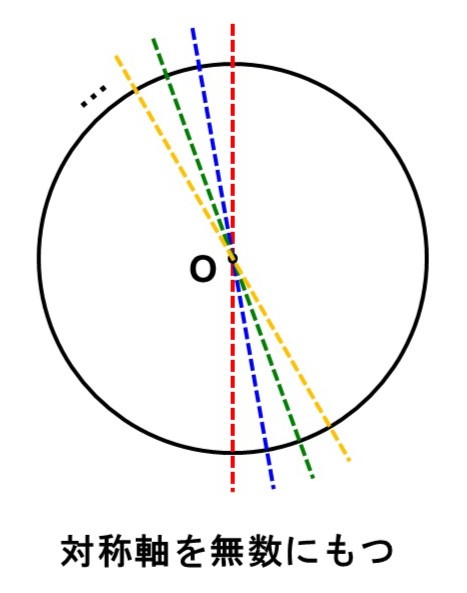
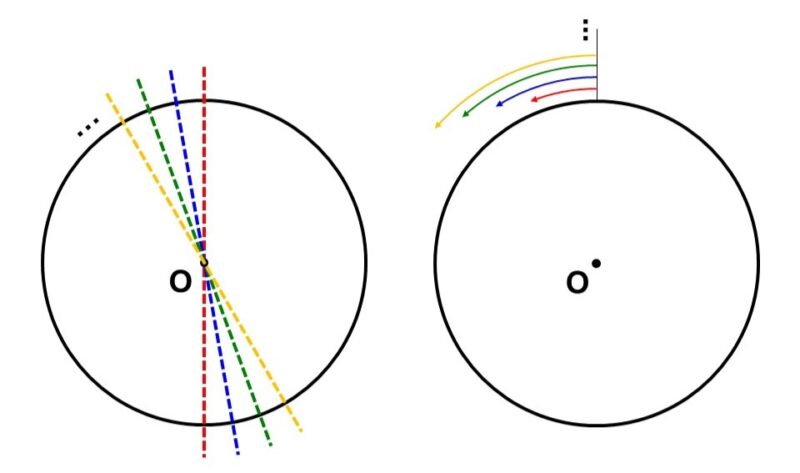
まずは「鏡映」。円の場合、どんな方向で鏡写しにしても元の円と重なるので、対称軸を無数にもつ線対称な図形であることがわかります。
次に「回転」。円の場合は回転させる角度にかかわらず元の円と重なるので、回転パターンを無数にもつ点対称な図形であることがわかります。
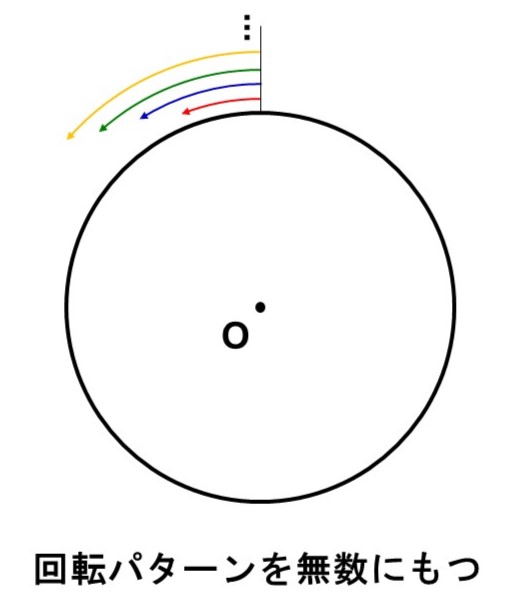
このように円は、無数の対称軸と回転パターンをもっているため、平面図形としてはもっとも対称性が高い図形であるといえます。そのため、車のタイヤをはじめ、様々なところで「円」が活用されています。
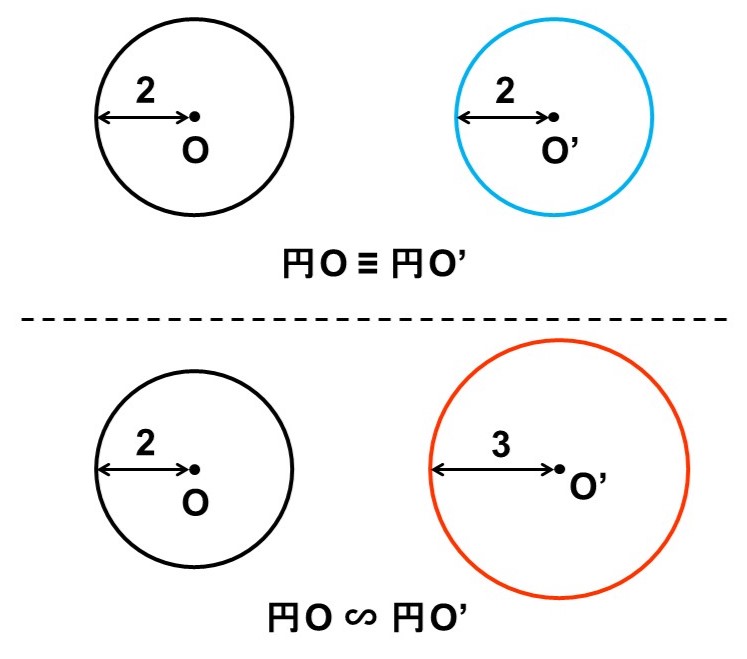
この対称性の高さゆえに、円については半径が同じなら「合同」、半径が異なっても「相似」の関係となります。
円から生まれる数 ― 円周率
円周率の定義
最高の対称性をもつ「円」は、その美しさから多くの人を魅了してきました。そして、円が人々を夢中にさせたもう一つの理由が、円周率(えんしゅうりつ)です。
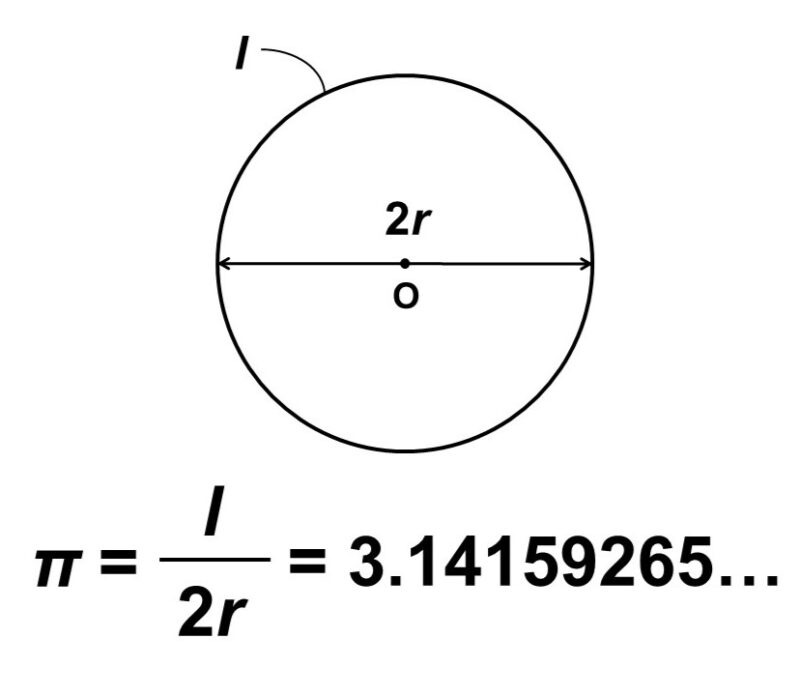
円周率とは、「直径の長さに対する円周の長さ」として定義される比率のことで、ギリシャ文字の$\pi$で表されます。
$\pi = \dfrac{\text{円周の長さ}}{\text{直径}}$
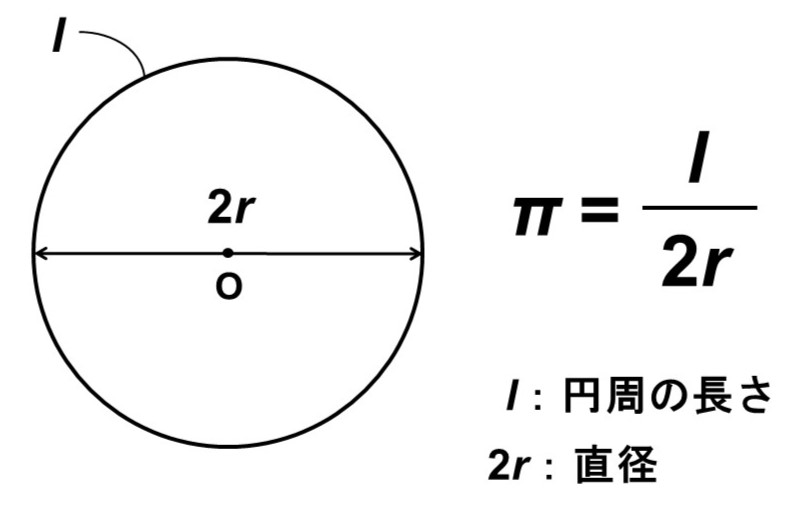
先に述べたように、円は大きさ(半径・直径)にかかわらず相似なので、この比率は円であれば必ず同じ値になります。
円周率$\pi$がもつ最大の特徴が「小数点以下の数に規則性がなく、どこまでも続いていく」ことです。
$\pi = 3.14159265…$
ランダムかつ絶えず数が続くということは、あなたの誕生日や電話番号の並びもどこかのタイミングで出てくるということでもあります[1]。これは驚きですよね。
自分で円周率を求めてみよう
円周率の定義は(円周の長さ)÷(直径)ですから、これにしたがって計算すれば、自分で円周率の値を求めることができるはずです。そこで、まてがめ自ら一つ実験をしてみました。
用意するのはトイレットペーパーの芯です。上から見るとちょうど円形になっているので、これを使えば円周率を計算できます[2]。

まずは直径を測定します。ちなみに今回は、「ノギス」と呼ばれる、円の外径や内径を測ることができる特殊な定規を使っています。

つづいて、円周の長さを測定します。これは、芯を切り開くことで簡単に測れます。

あとは、定義にしたがって計算するだけです。トイレットペーパーの芯7本分を測定した結果、次のようになりました。
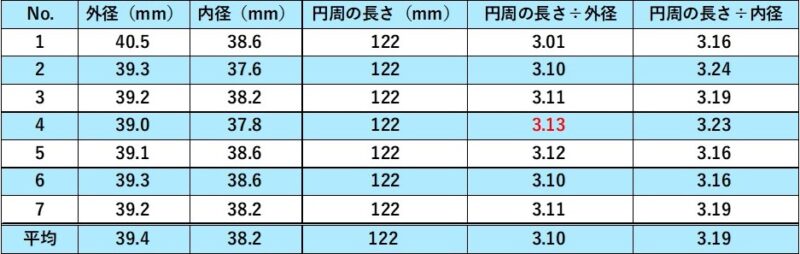
外径の値を使った場合と内径の値を使った場合の両方で計算してみましたが、小数点第1位(3.1)までは難なく求めることができました。円周率が「3よりも大きい値である」ということがよくわかります。
芯のゆがみや測定の誤差、測れる値の桁数が少ないこともあり、小数点第2位以下の算出にはいたりませんでした(もっとも近い値では3.13という値が出ました)。
アルキメデスの方法
一方、古代ギリシャ人のアルキメデスは全く別の方法で円周率を見積もろうとしました[1]。
例えば、半径1の円に対して、2つの正六角形を内側と外側に接するようにおきます。
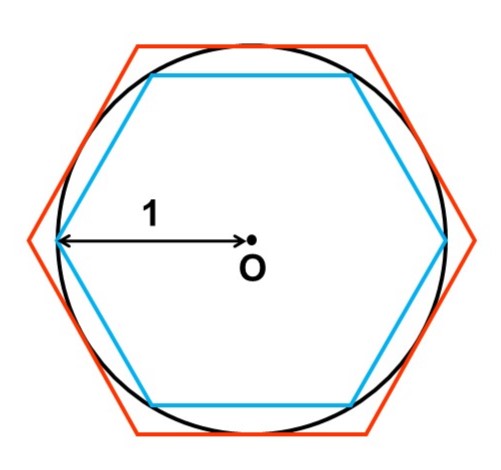
すると、周の長さは
内側の正六角形 < 円 < 外側の正六角形
という大小関係になります。
円周率の定義から、円周の長さは(円周率)×(直径)と書ける(後ほど改めて解説)ので、半径1の円周の長さは次のように計算できます。
$\pi \times (1 \times 2) = 2 \pi$
一方、内側の正六角形の周の長さを$l_\text{in}$、外側の正六角形の周の長さを$l_\text{out}$と表すことにすると、先ほどの大小関係は次のように簡単に表せます。
$l_\text{in} < 2 \pi < l_\text{out}$
この関係は、それぞれを÷2しても保たれますから
$\dfrac{l_\text{in}}{2} < \pi < \dfrac{l_\text{out}}{2}$ <*>
となり、円周率$\pi$の値が上と下でおさえられます。
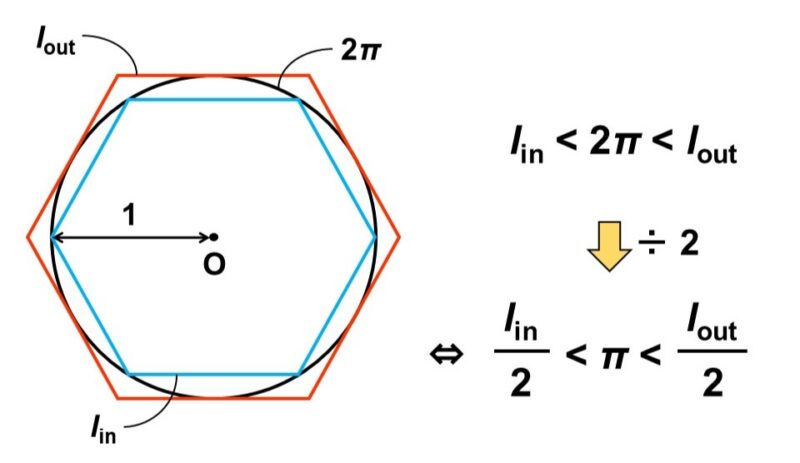
ところで、正多角形は同じ長さの辺からなる図形なので、その周の長さは図形的に求めることができます。つまり、2つの正六角形の周の長さ$l_\text{in}$, $l_\text{out}$は次のようにして計算できます。
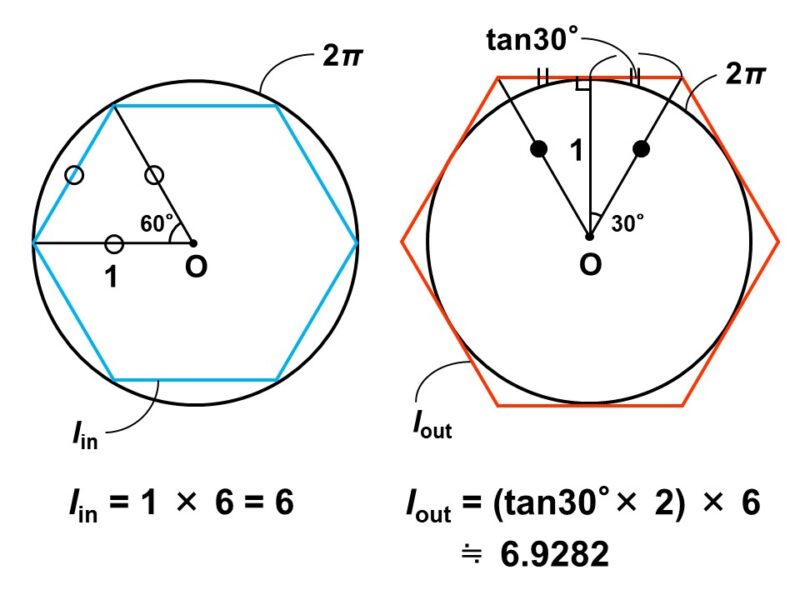
これより<*>は
$\dfrac{6}{2} = 3 < \pi < 3.4641 = \dfrac{6.9282}{2}$
となり、円周率$\pi$は3よりも大きい($\pi$ = 3.〇〇…)であることが決まります。
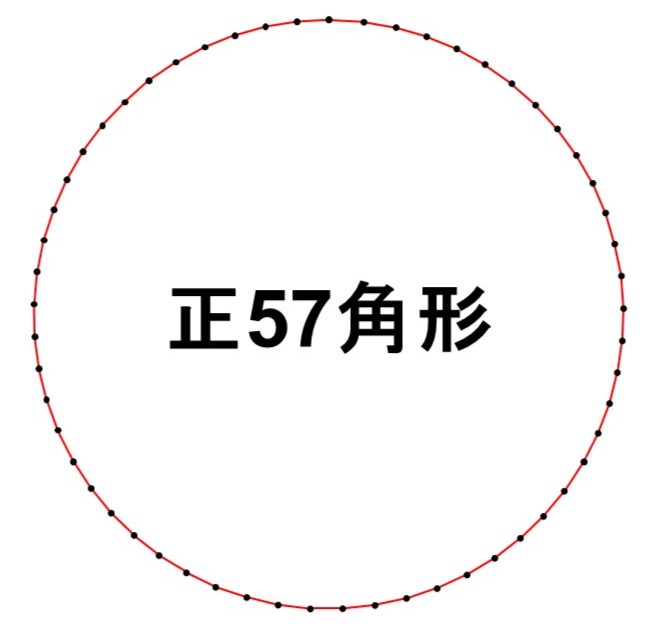
あとは、正多角形の角を増やしていき(正六角形 → 正七角形 → 正八角形 → …)、上と下からおさえる値の桁数を上げていけば、より正確に円周率の値を見積もることができます。この考え方、練習問題T8でも出てきましたね。
この方法は「測る」という操作がなく、理論上何桁でも調べることができるという点で最初の方法よりも優れています。
円周率を使って円を調べよう
ここまで円周率$\pi$については長々と話してきましたが、結局のところ、円周率=円という図形を形作るための情報がつまった数とイメージしておいてください。つまり、円周率を使えば、円についていろいろなことがわかるわけです。
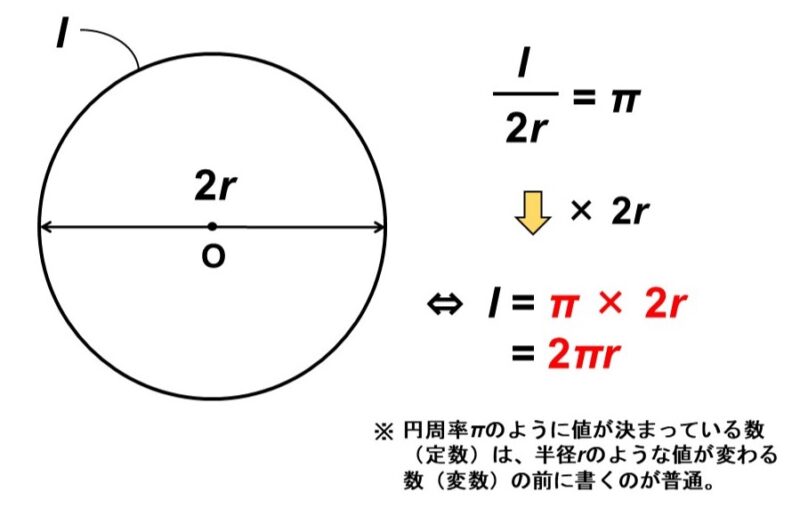
円周の長さ
円周率$\pi$の定義は
$\pi = \dfrac{\text{円周の長さ}}{\text{直径}}$
なので、逆に円周の長さは(円周率)×(直径)で求めることができます。
(例)
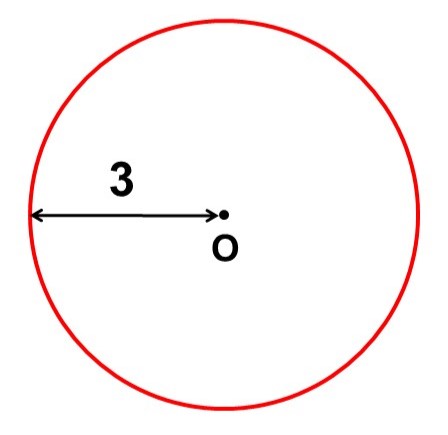
半径3の円Oの周の長さは、
$\begin{align}
\pi \times (2 \times 3) &\fallingdotseq 3.14 \times 6 \\[1.5ex]
&= 18.84
\end{align}$
円の面積
33Fで面積について学んでいますが、円の面積についてはどう考えればよいでしょうか?
一番問題なのが、円が「曲線でできた図形」であるということです。このままでは前回学んだことが使えそうにありません。
そこで、次のような工夫をしてみましょう[1]。まず、円をケーキのように8等分します。
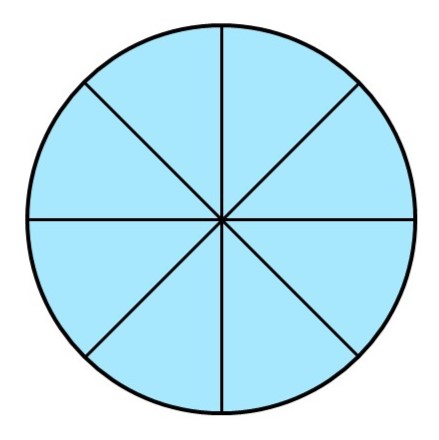
すると、分けた部分が二等辺三角形のように見えますね。続いて、分けた部分を次のように並べてみます。
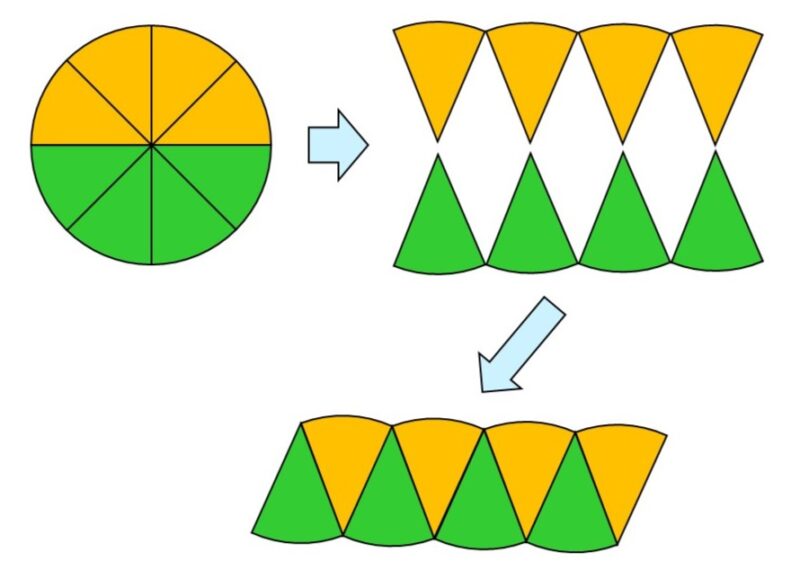
「合同な三角形が組み合わさると平行四辺形になる」という話を31Fでしましたが、同じようにして平行四辺形のような図形を作ることができるわけです。
これをもっと平行四辺形に近づけるには、初めに円をもっと細かくすればよいですね。
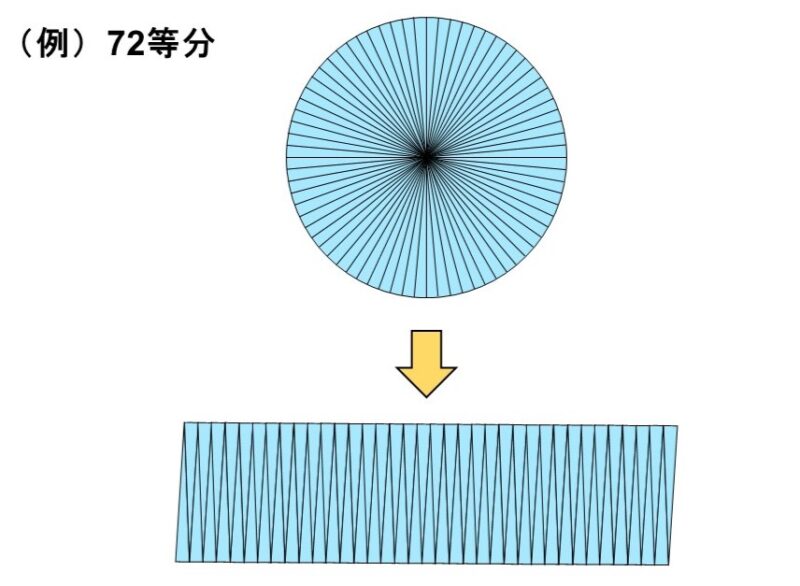
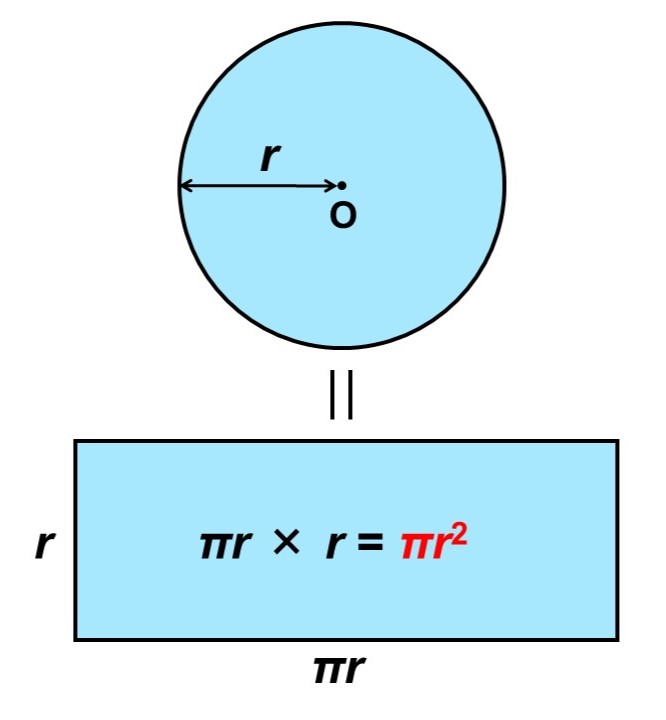
平行四辺形をへて、少しずつ長方形に近づいてきていることもわかりますね。このようにして、円を限りなく細かくしていくと、最終的には次のような長方形になります。
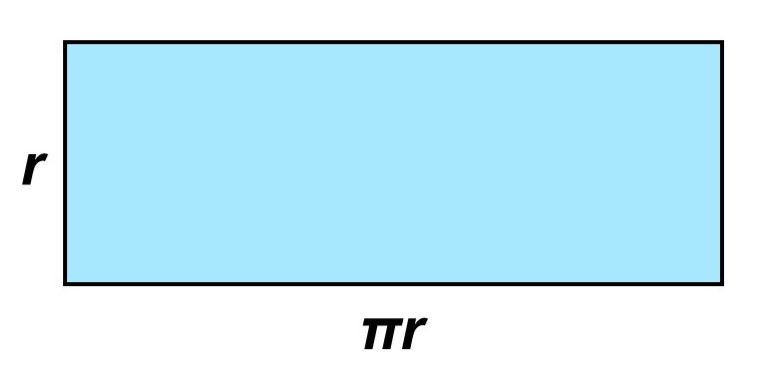
この長方形は底辺が円周の半分($\pi r$)、高さが半径($r$)になっているので、面積は
$\pi r \times r = \pi r^2$
となります。つまり、円の面積は(円周率)×(半径)2で求めることができます。
(例)
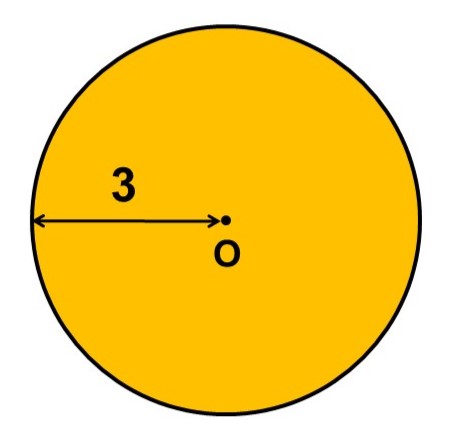
半径3の円Oの面積は
$\begin{align}
\pi \times 3^2 &\fallingdotseq 3.14 \times 9 \\[1.5ex]
&= 28.26
\end{align}$
まとめ
今回は円についての基本を学びました。最後に大切なポイントだけ簡単にまとめておきます。
- 円はもっとも対称性の高い図形である。
- 円周率$\pi$は(円周の長さ)÷(直径)で定義される比率で、小数点以下が不規則に続いていく数である。
- 円周率は「円についての情報がつまった数」であり、円周の長さや円の面積を求めるのに使うことができる。
円は、三角形と並んで平面図形の基礎となる図形であり、数学の面白さがたくさんつまった図形でもあります。
特に円周率に関する話は、ここに紹介した内容以外にも興味深いものがまだまだあるので、ぜひ自分で調べてみて、数学を楽しむきっかけにしてもらえればと思います。
今回はここまでです。お疲れ様でした!
参考資料
[1] Newton別冊 奥深き「カタチ」をめぐる数学 数学の世界 図形編 改訂第2版 (荒木義明, 市原一裕, 木村俊一, 河野俊丈, 笹川崇男, 下川航也, 杉原厚吉, 杉本晃久, 高橋大介, 高安秀樹, 徳山豪, 野老朝雄, 中村誠, 鳴川肇, 根上生也, 藤田伸, 松原隆彦)
[2] トイレットペーパーの芯を用いて円周率を求める実験については、横山明日希先生(@asunokibou)のツイートを参考にさせていただきました。
[3] Google Cloud上で100兆桁の円周率を計算 (Google Cloud 公式ブログ)