こんにちは、まてがめです。
前回は、分数の大小を比べるために必要な道具である「素因数分解」と「約分・通分」について学びました。
分数を扱っていくために必要なものはそろったので、今回から分数の計算に入っていきましょう。まずは分数の足し算・引き算について学びます。
分数の足し算・引き算でよくある間違いの一つに「分母同士と分子同士を計算してしまう」というものがありますが、今回の内容を見てもらえば「分母をそろえた上で分子同士を計算する」理由がわかってもらえるはずです。
分数の足し算
分母が同じ場合
具体例を考えてみましょう。
$\frac{2}{5}$ Lの水が入っているペットボトルと$\frac{3}{5}$ Lの水が入っているペットボトルがあったので、中身をじょうろに入れて使うことにした。
この時、じょうろに入る水は何Lになるか?
式を立てると、次のようになりますね。
$\dfrac{2}{5} + \dfrac{3}{5}$
さて、これはどう計算すればよいでしょうか?ここで分数が「数」であり「割り算」でもあることを使ってみます。この式を「割り算」に書きかえると、
$2 \div 5 + 3 \div 5$
となります。もしここで「計算できそう!」と思えた方は、四則演算がかなり身についてきています。
この式、分配法則が使えそうな気がしませんか?(「11F 四則演算(加減乗除)のまとめ」では、掛け算・割り算における分配法則の使い方を解説しているので、ぜひチェックしてみてください。)
もう一度おさらいしておくと、掛け算や割り算において同じ数が散っているような時は、分配法則を使うことでまとめることができます。すなわち、今回は次のように変形できます。
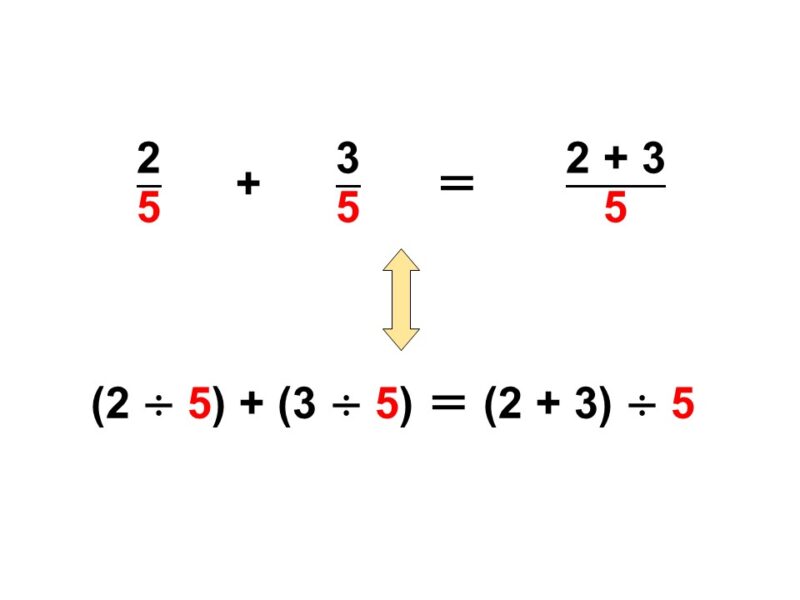
$2 \div 5+3 \div 5 = (2 + 3) \div 5$
よって、
$\begin{align}
2 \div 5 + 3 \div 5 & = (2 + 3) \div 5 \\[1.5ex]
& = 5 \div 5 \\[1.5ex]
& = 1
\end{align}$
なので、答えは1 Lとなります。
ここまでの話を踏まえ、分数に戻って考えてみると、次のような計算ができることになります。
$\begin{align}
\dfrac{2}{5} + \dfrac{3}{5} & = \dfrac{2 + 3}{5} \\[1.5ex]
& = \dfrac{5}{5} \\[1.5ex]
& = 1
\end{align}$
つまり分数の足し算は、分母がそろっていれば分子同士を足せばよく、それは分配法則が基になっているということです。
分母が異なる場合
分母が異なる場合ではどうでしょうか?次の例を見てみましょう。
ある学校には運動系の部活と文化系の部活がある。運動系の部活に入っている学生は全体の$\frac{3}{5}$、文化系の部活に入っている学生は全体の$\frac{2}{7}$だという。
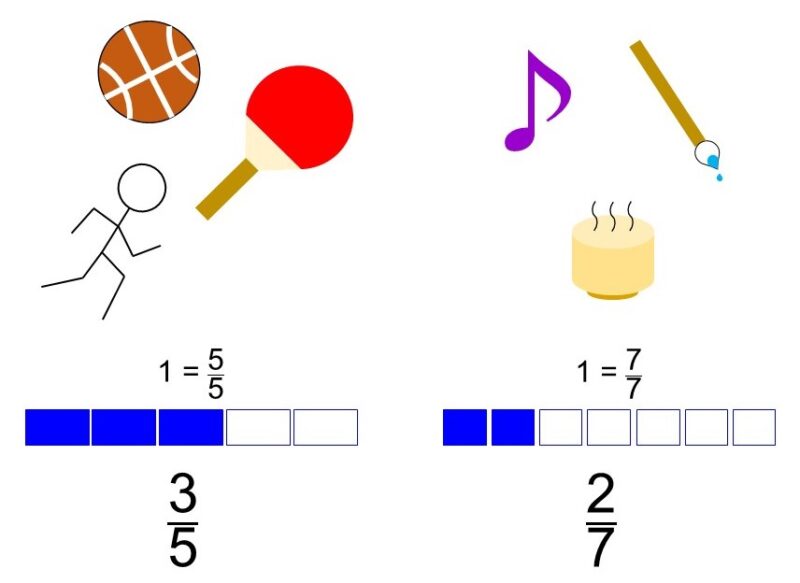
この時、部活に入っている学生は全体のいくらでしょうか?
部活には運動系と文化系があり、それぞれの割合が分かっているので、ひとまず足し算として式を立てることができます。
$\dfrac{3}{5} + \dfrac{2}{7}$
さっそく計算していきたいのですが、今度は分母がそろっていません。そこで、先ほどと同じ話にするため、分母を同じにする必要があります。
こんな時に役立つのが前回学んだ通分です。通分はまさしく「分数の分母をそろえる操作」ですから、こういった分数の足し算を行うには欠かせません。
通分を行うには「分母を見比べてお互いに足りていないものを補う」のがコツでした。見てみると、$\frac{3}{5}$の分母には7が、$\frac{2}{7}$の分母には5が足りていません。
そして分数は「分母と分子に同じ数を掛けても変わらない」という性質があります。なので、足りないものを分母に掛ける時は、忘れずに分子にも掛けましょう。$\frac{3}{5}$の分母と分子に7を、$\frac{2}{7}$の分母と分子に5を掛けると次のようになります。
$\begin{align}
\dfrac{3}{5} + \dfrac{2}{7} & = \dfrac{3 \times 7}{5 \times 7} + \dfrac{2 \times 5}{7 \times 5} \\[1.5ex]
& = \dfrac{21}{35} + \dfrac{10}{35}
\end{align}$
分母が35($= 5 \times 7$)にそろいました。これで、じょうろの時と同じように計算できますね。
$\begin{align}
\dfrac{3}{5} + \dfrac{2}{7} & = \dfrac{21}{35} + \dfrac{10}{35} \\[1.5ex]
& = \dfrac{21 + 10}{35} \\[1.5ex]
& = \dfrac{31}{35}
\end{align}$
よって、答えは全体の$\frac{31}{35}$となります。これはすなわち「全校生徒数を35等分したうちの31個分の割合で」学生は部活に入っていることになります(結構な割合ですね)。
分数の引き算
分数の引き算についても、基本的なやり方は足し算と同じですが、念のため例を使って確認しておきましょう。
手元にひもが$\frac{5}{6}$ m分があったので、このうち$\frac{3}{4}$ mを工作に使った。
この時、残ったひもは何mになるか?
式は次のようになりますね。
$\dfrac{5}{6}-\dfrac{3}{4}$
計算の手順は先ほどと同じく、「通分 → 分配法則を使って分子同士を計算」でOKです。
最初は通分です。ここは先ほどと違って分母がどちらも素数ではないので、まず素因数分解(素数の積に直すこと)を行った上でお互いの足りない分を確認するようにしましょう。分母の6と4をそれぞれ素因数分解します。
$6 = 2 \times 3$ $4 = 2 \times 2$
見比べてみると、$\frac{5}{6}$の分母には2が1つ、$\frac{3}{4}$の分母には3が1つ足りないので、$\frac{5}{6}$の分母・分子に2を、$\frac{3}{4}$の分母・分子に3を掛けると、
$\begin{align}
\dfrac{5}{6}-\dfrac{3}{4} & = \dfrac{5 \times 2}{6 \times 2}-\dfrac{3 \times 3}{4 \times 3} \\[1.5ex]
& = \dfrac{10}{12}-\dfrac{9}{12}
\end{align}$
分母が12($= 2 \times 2 \times 3$)にそろったので、分子をまとめて計算しましょう。
$\begin{align}
\dfrac{5}{6}-\dfrac{3}{4} & = \dfrac{10}{12}-\dfrac{9}{12} \\[1.5ex]
& = \dfrac{10-9}{12} \\[1.5ex]
& = \dfrac{1}{12}
\end{align}$
よって、答えは$\frac{1}{12}$ mですね。
計算に自然数が出てきた時は?
状況によっては自然数(1, 2, 3, …)と分数の計算になることもあります。その場合は一度自然数を分数に直してから計算するようにしましょう。
例として、次の式を計算してみます。
$5 + \dfrac{2}{3}$
この場合、自然数である5を一度分数にします。相手の分数は分母が3なので、分母は3にします。
分子はというと、(自然数)×(そろえる分母)で求まります。分数は「割り算」であり、割り算 ⇔ 掛け算だからですね。つまり、15($= 5 \times 3$)です。
ということで、式は次のようにできます。
$5 + \dfrac{2}{3} = \dfrac{15}{3} + \dfrac{2}{3}$
すでに分母はそろえてあるので、あとは同じように計算すれば大丈夫です。
$\begin{align}
5 + \dfrac{2}{3} & = \dfrac{15}{3} + \dfrac{2}{3} \\[1.5ex]
& = \dfrac{15 + 2}{3} \\[1.5ex]
& = \dfrac{17}{3}
\end{align}$
まとめ
今回は「分数の足し算・引き算」について学びました。計算の仕方をまとめると次のようになります。
- 通分する(必要であれば分母は素因数分解して備える)
- 分子同士をまとめる(=分配法則)
- 分子を計算する
この手順を覚えておいた上で、ちゃんと足し算・引き算ができれば、必ず答えにたどり着けます。
2番目にも書いたように、分配法則が使われているというのがポイントです。だからこそ、最初に「分母をそろえよう(通分しよう)」と思うわけですね。
今回はここまでです。お疲れさまでした!