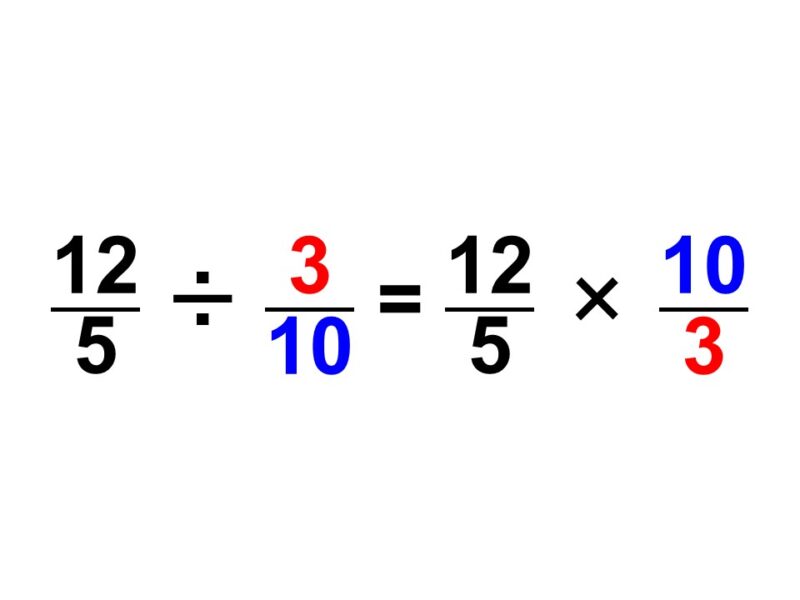こんにちは、まてがめです。
前回は、「分数の足し算・引き算」について学びました。分母をそろえて分子を計算する理由は分配法則を使いたいからでしたね。
前回に続き、今回は分数の掛け算・割り算について学んでいきます。
ここも多くの方がつまづきやすいところです。特に割り算では、突然「分母と分子を入れかえる」という奇妙な技が出てくるので混乱しやすいです(まてがめも小学生の時に先生を質問攻めにしました)。
この部分についてもしっかり説明していきますので一緒に頑張りましょう!
分数と自然数の掛け算・割り算
分数同士の計算に入る前に、準備として先に分数と自然数の計算を考えてみます。
分数に「ある数を掛ける」ということ、分数を「ある数で割る」ということが何を意味しているのか一度確認しておきましょう。
分数と自然数の掛け算
次の式を計算してみましょう。
$\dfrac{2}{5} \times 2$
これを図にしてみると次のようになりますね。
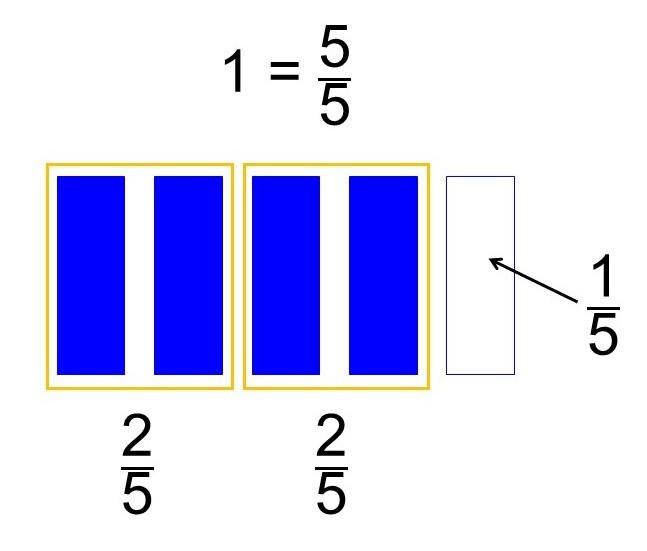
答えが$\frac{4}{5}$になるというのは図を見ればわかりますが、式と図をどう理解するのかが大切です。
最初の式をそのまま言葉で表すならば、「$\frac{2}{5}$が2個ある」ということになります。そして、その答えが$\frac{4}{5}$になるということは、次のような計算を行っていることになりそうです。
$\dfrac{2}{5} \times 2 = \dfrac{2 \times 2}{5} = \dfrac{4}{5}$
この真ん中の式を言葉で表すならば、「5等分したものが2×2個だけある」という言い方ができますね(前回学んだ割合の考え方を思い出してみてください)。確かに図を見てもそういう考え方ができそうです。
このように分数と自然数の掛け算では、(分子)×(自然数)の形で計算できます。
分数と自然数の割り算
次の式を計算してみましょう。
$\dfrac{3}{5} \div 2$
こちらも図にしてみると次のようになります。
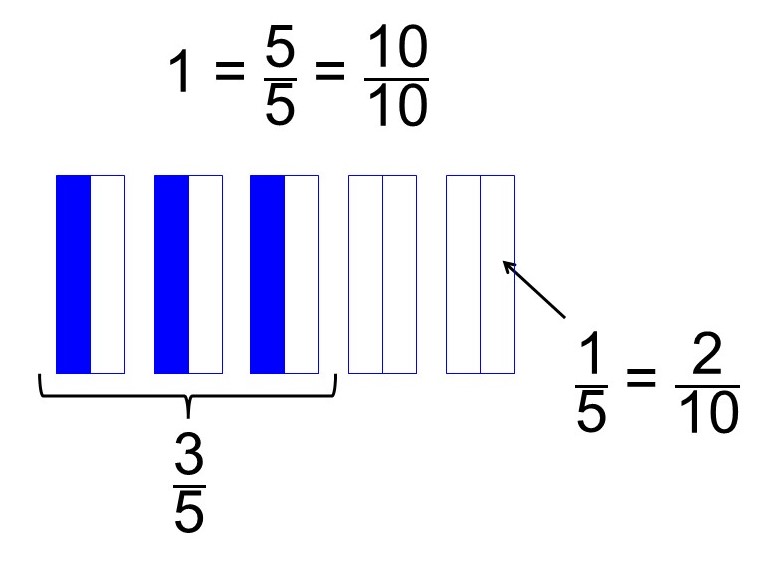
図からこの答えは$\frac{3}{10}$とわかりますが、ここでも式と図の意味を考えてみます。
まず最初の式はそのまま「$\frac{3}{5}$を2等分する」と理解できます。その答えが$\frac{3}{10}$ということは、今度は次のような計算になっていると考えられそうです。
$\dfrac{3}{5} \div 2 = \dfrac{3}{5 \times 2} = \dfrac{3}{10}$
この真ん中の式は「5×2等分したものが3個分ある」という言い方ができます。確かに図を見ると、5等分したものをさらに2等分しているので$5\times2=10$等分してから3個数えたという理解もできますね。
このように分数と自然数の割り算では、(分母)×(自然数)の形で計算できます。
- (分数)×(自然数) → (分子)×(自然数)の形で計算できる
- (分数)÷(自然数) → (分母)×(自然数)の形で計算できる
分数同士の掛け算
準備ができたので、まずは分数同士の掛け算について、例を使って見ていきましょう。
$\frac{8}{9}$ L入ったオレンジジュースがあったので、これを遊びに来ていた友達と一緒に飲んだところ、その$\frac{3}{4}$を消費した。
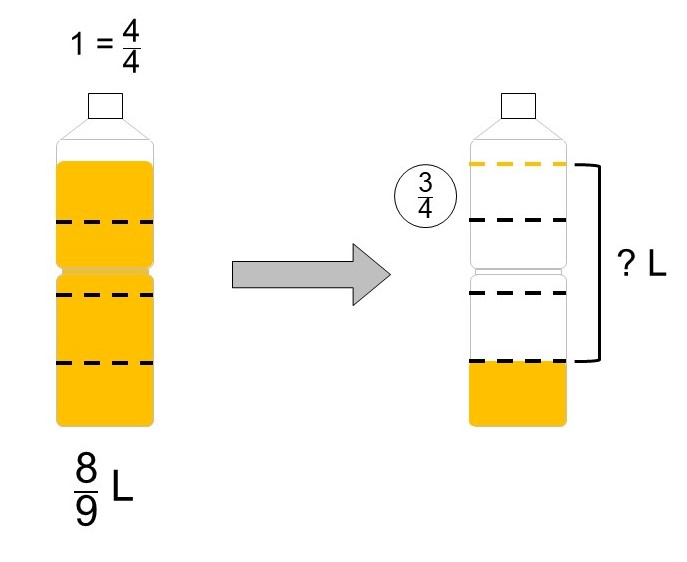
この時、消費したジュースは何Lになるか?
この問題に対する考え方は2通りあります(※本質的にはどちらも同じです)。
(1) 「掛け算」として考える
掛け算は基本的に「同じものがどれだけあるか」という見方で式を立てますよね。この「どれだけ」という言葉が示す範囲を自然数から分数まで広げてあげるわけです。
すると、「($\frac{8}{9}$ Lの)ジュースが$\frac{3}{4}$だけある」というのは掛け算として式が立てられます。
$\dfrac{8}{9} \times \dfrac{3}{4}$
こちらは状況をそのまま式にしているので、とてもシンプルです。あとはこれをどう計算するかですね。
(2) 「割合の考え方」を使う
$\frac{3}{4}$ということは、$\frac{8}{9}$ Lを4等分したうちの3つ分だけジュースを飲んだと考えることができます。
$\dfrac{8}{9} \div4 \times 3$
先ほど分数と自然数の掛け算・割り算について学びましたから、これを使って計算してみましょう。
まず、÷4の部分は(分母)×4の形にできます。
$\dfrac{8}{9} \div 4 \times 3=\dfrac{8}{9 \times 4} \times 3$
続いて、×3の部分は(分子)×3の形にできます。
$\begin{align}
\dfrac{8}{9} \div 4 \times 3 & = \dfrac{8}{9 \times 4} \times 3 \\[1.5ex]
& = \dfrac{8 \times 3}{9 \times 4}
\end{align}$
このまま分母と分子を計算しても良いですが、先に約分しておいた方が楽です(素因数分解してもよいですが、このくらいなら$3 \times 4=12$で分母と分子を割ればよいことに気づけますね)。
$\begin{align}
\dfrac{8}{9} \div 4 \times 3 & = \dfrac{8 \times 3}{9 \times 4} \\[1.5ex]
& = \dfrac{(2 \times 4 \times 3) \div 12}{(3 \times 3 \times 4) \div 12} \\[1.5ex]
& = \dfrac{2}{3}
\end{align}$
よって、消費したジュースは$\frac{2}{3}$ Lです。
さて、2通りの考え方を見てきましたが、これらを踏まえると次の等式が成り立っていることがわかります。
$\dfrac{8}{9} \times \dfrac{3}{4} = \dfrac{8 \times 3}{9 \times 4}(= \dfrac{2}{3})$
このように分数同士の掛け算では、(分母)×(分母)と(分子)×(分子)の形にして計算することができます。
分数同士の割り算
続いて、分数同士の割り算を見ていきます。例を次に示します。
今、長さ$\frac{12}{5}$ mの針金を切り、$\frac{3}{10}$ mの針金を作れるだけ作りたい。
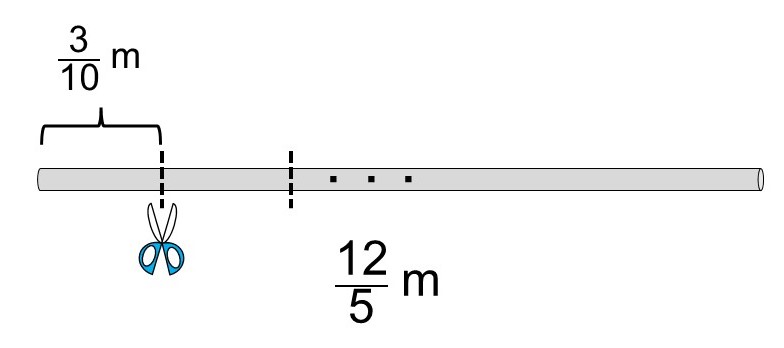
この時、できる針金の本数は何本になるか?
針金を同じ長さで切り出していって小さい針金を作ることになるので、割り算の式で表すことができます。
$\dfrac{12}{5} \div \dfrac{3}{10}$
さっそく計算していくために、これまでに学んだことをうまく使いながら計算できる形にしてましょう。
まず割り算は分数にできるので、これを分数にしてしまいます。
$\dfrac{12}{5} \div \dfrac{3}{10} = \dfrac{\dfrac{12}{5}}{\dfrac{3}{10}}$
見た目はすごいですが、それぞれの分数自体が「数」なので、書き方としては問題ありません。
ただ、このままでは先に進めないので、「分数の分母と分子に同じ数を掛けてもよい」という性質を利用して、1つ細工をします。それは「分母の数の逆数(分母と分子を入れ替えた数)を分母と分子に掛ける」ことです。どういうことかというと、次のような操作を行うということです。
$\dfrac{\dfrac{12}{5}}{\dfrac{3}{10}} = \dfrac{\dfrac{12}{5} \times \dfrac{10}{3}}{\dfrac{3}{10} \times \dfrac{10}{3}}$
するとどうなるでしょうか?先ほど学んだばかりの掛け算を使って、分母を計算してみると、
$\dfrac{3}{10} \times \dfrac{10}{3} = \dfrac{3 \times 10}{10 \times 3} = 1$
となるので、先ほどの大きな分数は
$\dfrac{\dfrac{12}{5}}{\dfrac{3}{10}} = \dfrac{\dfrac{12}{5} \times \dfrac{10}{3}}{1} = \dfrac{12}{5} \times \dfrac{10}{3}$
と簡単な形にすることができます(分母が1ということは1で割ることと同じですからね)。
ここまでの話をまとめると、次が成り立つということになります。
$\dfrac{12}{5} \div \dfrac{3}{10} = \dfrac{12}{5} \times \dfrac{10}{3}$
元々割り算を計算しようとしていましたが、掛け算の形にすることができました。このように、分数で割ることは「その分数の逆数でかけること」と同じことを意味しています。
計算の続きですが、こうなってしまえばあとは分数の掛け算として計算するだけです。
$\begin{align}
\dfrac{12}{5} \div \dfrac{3}{10} & = \dfrac{12}{5} \times \dfrac{10}{3} \\[1.5ex]
& = \dfrac{12 \times 10}{5 \times 3} \\[1.5ex]
& = \dfrac{(3 \times 4 \times 2 \times 5) \div 15}{(5 \times 3) \div 15} \\[1.5ex]
& =\dfrac{8}{1} = 8
\end{align}$
よって、答えは8本となります。
まとめ
今回は分数の掛け算・割り算について学びました。大切な内容がたくさんあったのでまとめておきます。
- (分数)×(自然数) → (分子)×(自然数)の形で計算できる
- (分数)÷(自然数) → (分母)×(自然数)の形で計算できる
- 分数同士の掛け算では、$\dfrac{\text{(分子)×(分子)}}{\text{(分母)×(分母)}}$の形にして計算できる
- 分数で割る時は、その逆数の掛け算にできる
「割り算では分数の逆数を掛ける」というのはもちろん覚えておきたいポイントですが、それを導くために行った「逆数を分母と分子に掛ける」という操作は今後もいろんな場面で役立つので、こちらもぜひテクニックとして覚えておいてください。
今回はここまでです。お疲れさまでした!