こんにちは、まてがめです。
ここまで2階にわたり、「分数の計算」について学んできました。
「これで分数が扱えるようになった!」と喜びたいところなのですが、まだ少し足りません。実際、今のまま分数を使おうとすると、
「あれ、そもそもどうやって分数を使った式を立てればよいのかわからないな…」
ということがよく起こります。これは「どんな時にどんな量を分数として表すことができるのか」について、まだ理解が十分ではないからです。
そこで今回は、「分数がどんな場面で使えるのか」について着目して学んでいきます。
「分数が使える」=「割り算が使える」
ある場面において「分数が使える」ということは「割り算が使える」ということを意味しています。
一方、割り算と分数のそれぞれについて、こんなイメージはないでしょうか?
- 割り算…「個数や人数を等しく分ける」イメージ
- 分数…「小さなかたまり($\frac{1}{\text{○}}$)を数える」イメージ
このイメージの違いは、分数を使った表現や考え方でわからなくなってしまう原因の1つであるように思います。異なるイメージを持つのはよいのですが、割り算も分数も本質は同じです。なので、割り算が出てきた時には分数を、分数が出てきた時には割り算を思い出してあげましょう。
「なぜ分数で表せるのだろう?」と思ったら、「割り算で考えると何を意味しているのだろうか?」と考えてみるといいですね。必要に応じて分数と割り算を行ったり来たりできると理解が深まりますよ。
…と前置きはここまでにして、分数が使える場面をさっそく見ていきましょう!
使い方1 割合
1つ目の使い方は割合(わりあい)です。これまでにも何度か出てきてはいるので、多少はなじみがあるでしょうか。
割合は「全体を1とみなした時に、そのうちのどのくらいを占めるか」考えるものです。一番分数らしい使い方とも言えます。
例を見てみましょう。
全校生徒450人のうち、180人は徒歩で通学しており、残りは自転車で通学している。
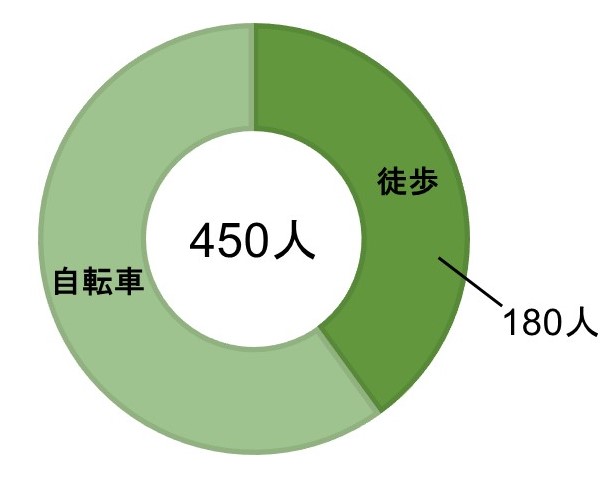
この時、徒歩で通学している生徒の割合は
$\begin{align}
& \hspace{13pt} \dfrac{180}{450} \\[1.5ex]
& = \dfrac{2 \times 2 \times 3 \times 3 \times 5}{2 \times 3 \times 3 \times 5 \times 5} \\[1.5ex]
& = \dfrac{2}{5}
\end{align}$
※今回は90($= 2 \times 3 \times 3 \times 5$)で約分できます。
では、この例における自転車で通学している学生の割合についても考えてみましょう。
この時、その人数を$450-180 = 270$と求めてから、
$\begin{align}
& \hspace{13pt} \dfrac{270}{450} \\[1.5ex]
& = \dfrac{2 \times 3 \times 3 \times 3 \times 5}{2 \times 3 \times 3 \times 5 \times 5} \\[1.5ex]
& = \dfrac{3}{5}
\end{align}$
としてもよいのですが、割合の性質をうまく使って楽をしましょう。
すなわち、全体が1なので、そこから徒歩通学者の割合である$\frac{2}{5}$を差し引きます。すると当然、答えは自転車通学者の割合になりますよね。
$\begin{align}
1-\dfrac{2}{5} & = \dfrac{5}{5}-\dfrac{2}{5} \\[1.5ex]
& = \dfrac{5-2}{5} \\[1.5ex]
& = \dfrac{3}{5}
\end{align}$
ちなみに割合という考え方は、百分率(%)という形でよく使われています。こちらでは、全体を1ではなく100(%)とみなして割合を考えます。
今回の例を百分率で表すと次のようになります。
- 徒歩…$\dfrac{2}{5} \times 100 = \dfrac{200}{5} = 40$%
- 自転車…$\dfrac{3}{5} \times 100 = \dfrac{300}{5}=60$%
使い方2 比率
2つ目の使い方は比率(ひりつ)です。次の例を見てください。
ある料理2人分に使うタレを作るのに、しょうゆを3 g、砂糖を2 g使った。
この時、しょうゆと砂糖の比は
3:2
また、しょうゆに対する砂糖の比率は
$\dfrac{2}{3}$
比または比率がわかっていると、同じものを異なるスケールで作る時に必要な数量を知ることができます。
例えば、この料理を4人分作りたいとします。その場合、もともとの2倍の人数分を作ることになるので、必要なしょうゆと砂糖もそれぞれ2倍すればよいとわかります。
- しょうゆ:$3 \times 2 = 6$ g
- 砂糖:$2 \times 2 = 4$ g
では、しょうゆ5 gを使って同じ料理を作りたい場合、砂糖は何g必要になるでしょうか?
これは比率を使うことで計算できます。今はしょうゆの量がわかっているので、しょうゆに対する砂糖の比率$\frac{2}{3}$を使うことで、
$5 \times \dfrac{2}{3} = \dfrac{10}{3}$ g
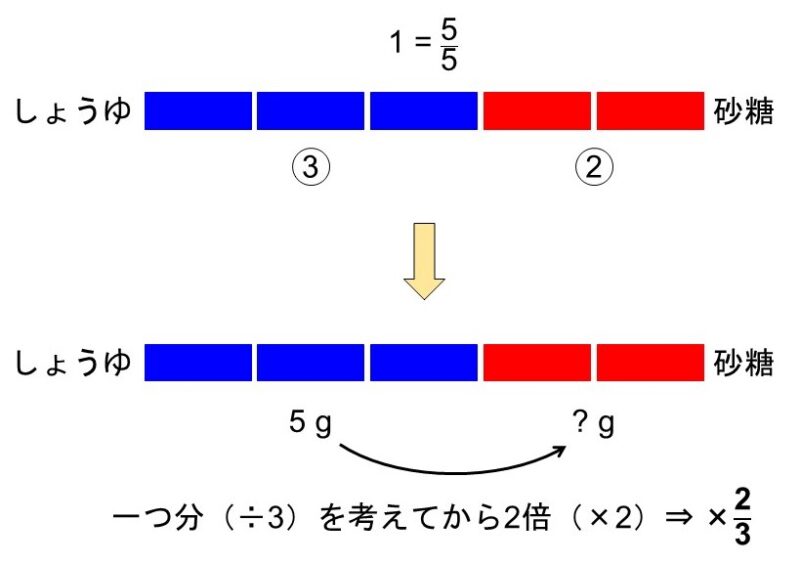
と求まります。「わかっている方を分母に、わからない方を分子に持ってきて比率とする」のがポイントです。
どう考えて計算をしているかというと、「しょうゆを3と見た時に砂糖は2になるから、量がわかっているしょうゆの量を一度3で割ってから2倍(=$\frac{2}{3}$倍)すると砂糖の量がわかる」といった感じです。
使い方3 確率
3つ目の使い方は確率(かくりつ)です。確率については、また別の機会に詳しく説明しますので、ここでは簡単に触れておきます。
確率は「ある出来事(事象)が起こる可能性がどのくらいか」を表したもので、
$\dfrac{\text{ある事象の数}}{\text{全ての事象の数}}$
と表すことができます。ただし、起こりうる全ての事象は、それぞれの起こる可能性が等しい(同様に確からしい)ものでなければなりません。
例を見てみましょう。
ジョーカーの含まれていない計52枚のトランプをよくシャッフルして、上から1枚目をめくって確認する。
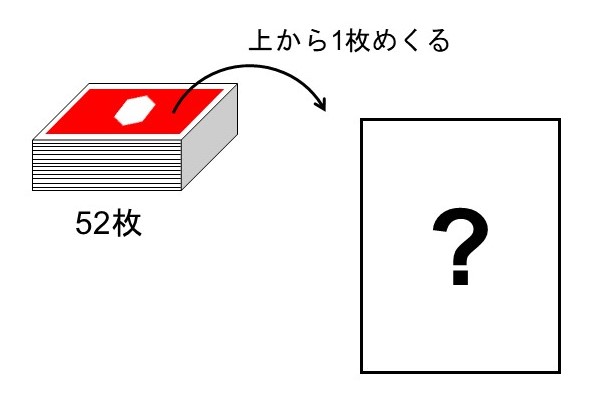
この時、起こりうる全ての事象(どんなカードが表になるか)は52通り。
これを踏まえて、次の確率を考えてみましょう。
(1) めくったカードが2である確率
めくった時に2となるのは、スペードの2・ハートの2・クラブの2・ダイヤの2の4通りなので、その確率は
$\dfrac{4}{52} = \dfrac{1}{13}$
となります。これはすなわち、「13回に1回はめくったカードが2になる可能性がある」ということであり、あくまで可能性の話です。
(2) めくったカードが絵札である確率
めくった時に絵札となるのは、「11~13の3通り」に対して「スペード~ダイヤの4通り」の計12通り($=3 \times 4$)なので、その確率は
$\dfrac{12}{52} = \dfrac{3}{13}$
となります(掛け算のところがわからない方はこちらを復習してみてください)。
今回は考えられる事象の数が多い分、先ほどよりも確率が大きい(起こりうる可能性が高い)ことがわかります。
使い方4 単位あたりの量
単位あたりの量は必ずしも答えが分数になるわけではないですが、分数で考えることが多いです。代表的なものを以下に示します。
速さ
$\dfrac{\text{距離}}{\text{時間}}$
で「単位時間あたりの移動距離(決まった時間でどれだけ移動するか)」を考えます。時間に対して距離を割りふるイメージです。
(例)
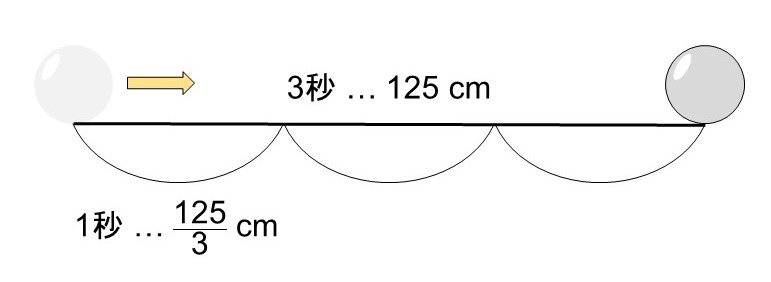
床の上で球を転がしたところ、3秒で125 cm進んだ。
この時の球の速さ(1秒間に進む距離)は
$(125 \div 3 =) \dfrac{125}{3}$ cm/秒
※単位を書く時もこのように / を使って分数のように表します。
密度
$\dfrac{\text{重量}}{\text{体積}}$
で「単位体積あたりの重量(決まった体積でどれだけの重さがあるか)」を考えます。体積に対して重量を割りふるイメージです。
(例)
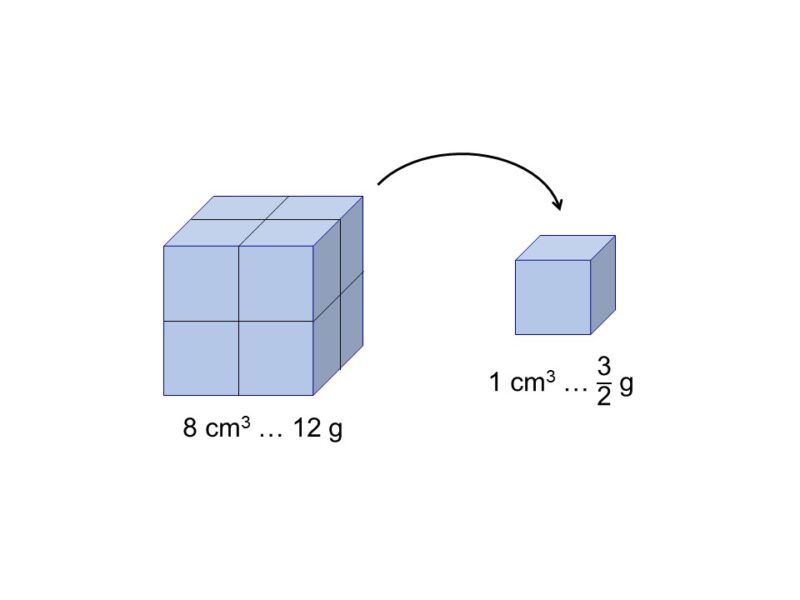
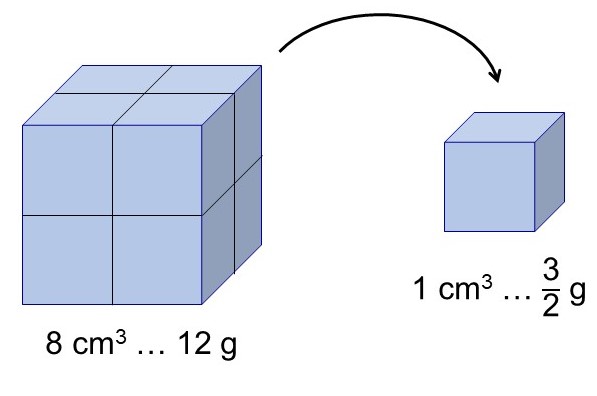
ここに体積が8 cm3、重さが12 gのブロックがある。
このブロックの密度(1 cm3あたりの重量)は
$(12 \div 8 =) \dfrac{12}{8} = \dfrac{3}{2}$ g/cm3
濃度
$\dfrac{\text{溶解量}}{\text{全体量}}$
で「単位量あたりの溶解量(決まった量にどれだけ溶けているか)」を考えます。全体量に対して溶解量を割りふるイメージです。
(例)
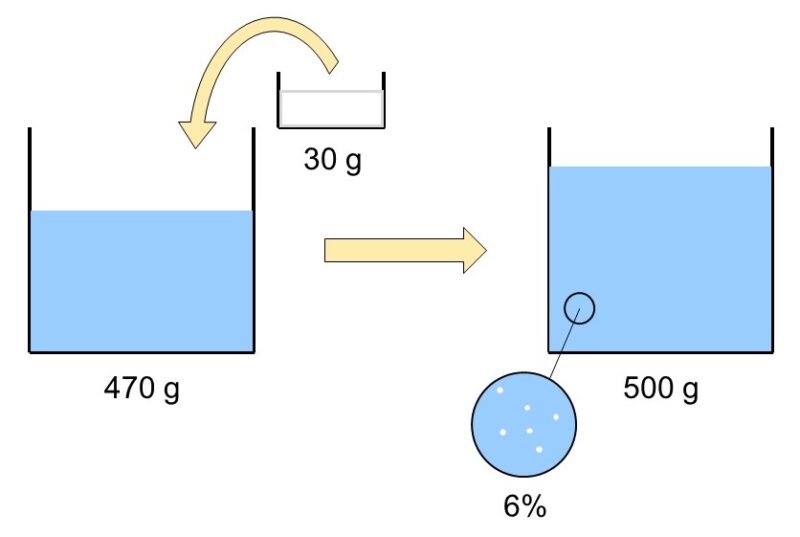
水470 gに塩30 gを入れてよく混ぜることで、食塩水500 gを作った。
この時、この食塩水の濃度(食塩水1 gにふくまれる塩の重量)は
$(30 \div 500 =) \dfrac{30}{500} = \dfrac{3}{50}$
※g/gになるので単位は書きません。
濃度については百分率で表すことも多いです。今回の例の場合は、
$\dfrac{3}{50} \times 100 = \dfrac{300}{50} = 6$%
となります。
まとめ
今回は分数の使い方について学びました。分数を使った考え方がピンとこない時は、割り算に戻って意味を考えるようにしましょう。
- 割合
- 比率
- 確率
- 単位あたりの量:速さ、密度、濃度
今回は代表的なものについてのみ解説しましたが、もちろんこの他にも多くの使い方があります。ただ、基本的にはこれらの仲間であることが多いです。
数学だけでなく物理や化学といった理学を学んでいく上では、どれも大切な考え方なので慣れておきましょう。
今回はここまでです。お疲れさまでした!