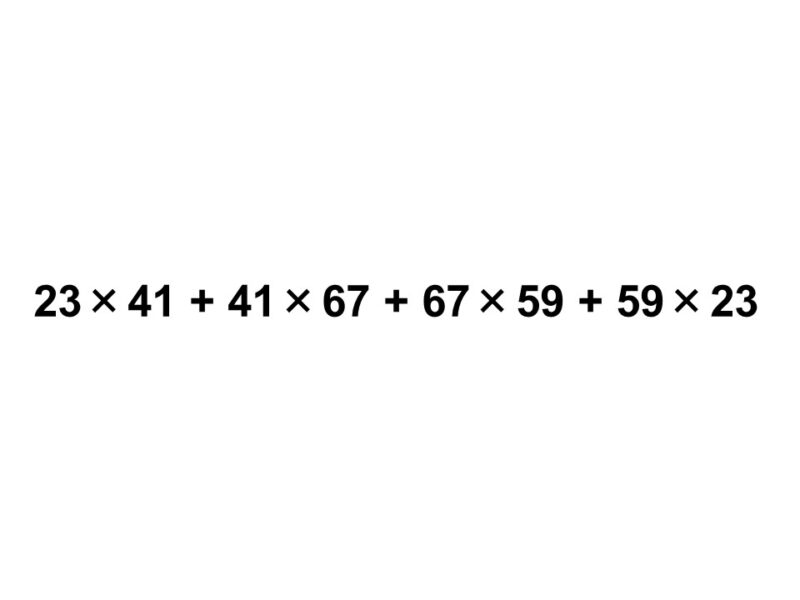今回の問題はこちらです。(※8Fまでの内容を理解していることが前提です!)
次の式を計算してください。
$23 \times 41 + 41 \times 67 + 67 \times 59 + 59 \times 23$
さて、あなたならどう計算しますか?
解き方1 「気合いだ!」…とにかく計算
「とにかく答えが出ればいいでしょ!」と考えて、気合いで計算する方法です。
計算の順番は掛け算→足し算なので、掛け算の部分を先に計算します。
$23 \times 41 = 943$
$41 \times 67 = 2747$
$67 \times 59 = 3953$
$59 \times 23 = 1357$
なので、
$\begin{align}
& \hspace{13pt} 23 \times 41 + 41 \times 67 + 67 \times 59 + 59 \times 23 \\[1.5ex]
& = 943 + 2747 + 3953 + 1357 \\[1.5ex]
& = 9000
\end{align}$
よって、答えは9000です。
この方法の場合、掛け算の筆算や足し算の筆算が多く出てくるので、ていねいに計算しましょう。
解き方2 「楽したい!」…分配法則
「確かに気合いで計算できるけど、できるなら楽に計算したいな…」と思った方もいるでしょう。
そう思いながら式をよく見てみると、実は分配法則が使えることがわかります。例えば、前半の足し算で考えてみると、
$23 \times 41 + 41 \times 67 = 41 \times (23 + 67)$
と41でくくることができます。
そして、後半の足し算についても考えてみると、
$67 \times 59 + 59 \times 23 = 59 \times (67 + 23)$
と59でくくることができます。
したがって、
$\begin{align}
& \hspace{13pt} 23 \times 41 + 41 \times 67 + 67 \times 59 + 59 \times 23 \\[1.5ex]
& = 41 \times (23 + 67) + 59 \times (67 + 23) \\[1.5ex]
& = 41 \times 90 + 59 \times 90
\end{align}$
となりますが、ここでもう一度分配法則が使えることに気づければすばらしいです。すなわち、
$\begin{align}
& \hspace{13pt} 41 \times 90 + 59 \times 90 \\[1.5ex]
& = (41 + 59) \times 90 \\[1.5ex]
& = 100 \times 90 \\[1.5ex]
& = 9000
\end{align}$
と計算できます。こちらも筆算は出てきますが、90や100のようにきりの良い数が出てくるので計算はしやすいですね。
分配法則から因数分解・展開へ
解き方2から、次の等式が成り立つことがわかります。
$\begin{align}
& \hspace{13pt} 23 \times 41 + 41 \times 67 +67 \times 59 + 59 \times 23 \\[1.5ex]
& = (41 + 59) \times (23 + 67)
\end{align}$
このように、分配法則を使ってカッコの中以外には足し算や引き算のない掛け算の形にすることを因数分解(いんすうぶんかい)と呼びます。また、逆に分配法則を使って因数分解してある式をカッコのない形にすることを展開(てんかい)と呼びます。
今回の例では因数分解を使って計算を簡単にしたと言えますね。では、展開を使って計算を簡単にする例も見てみましょう。
$102 \times 98$
これを普通に計算しようとすると、おそらく筆算を使うでしょう。ですが、「どちらの数も100に近いな…100×100だったら簡単だったのに」とは思いませんか?
そこで、こんなふうに式を書きかえてみましょう。
$102 \times 98 = (100 + 2) \times (100-2)$
2つの数が100からどれだけ離れているかをカッコを使って書きました。続いて、展開を行います。分配法則を2回使えばOKです。
$\begin{align}
&\hspace{13pt} 102 \times 98 \\[1.5ex]
& = (100 + 2) \times (100-2) \\[1.5ex]
& = 100 \times (100-2) + 2 \times (100-2) \\[1.5ex]
& = 100 \times 100-100 \times 2 + 2 \times 100-2 \times 2 \\[1.5ex]
\end{align}$
すると、どうでしょうか?真ん中の$100 \times 2 = 200$が打ち消し合うので、
$\begin{align}
&\hspace{13pt} 102 \times 98 \\[1.5ex]
& = 100 \times 100-2 \times 2 \\[1.5ex]
& = 10000-4 \\[1.5ex]
& = 9996
\end{align}$
となります。筆算よりも計算が楽ですね。
このように因数分解や展開を使うと、筆算では手間のかかる計算を簡単な計算に直せることがあります。因数分解・展開は方程式を解く際にもよく使うので、ぜひ今のうちに頭のかたすみに置いておいてください(また改めて別の機会に解説します)。