こんにちは、まてがめです。
これまで5階にわたり、「分数」について学んできました。
分数は、私たちがいつも使う数である0や自然数(1, 2, 3, …)の間に存在する数ですが、こういった数を表す方法が実はもう一つあります。それが小数(しょうすう)です。
では、分数と小数は何が違うのでしょうか?今回は分数と小数の違いやその変換方法について学んでいきます。
小数とは?
小数(しょうすう)では、0や自然数(1, 2, 3, …)の間に存在する数を10進法を使って表します。そしてそのために小数点というものを使います。
具体的には、小数点を境にして一の位よりも小さい位を用意します。各位の呼び方ですが、小数点に近い方から順に「小数点第1位、第2位、第3位、…」と呼びます。
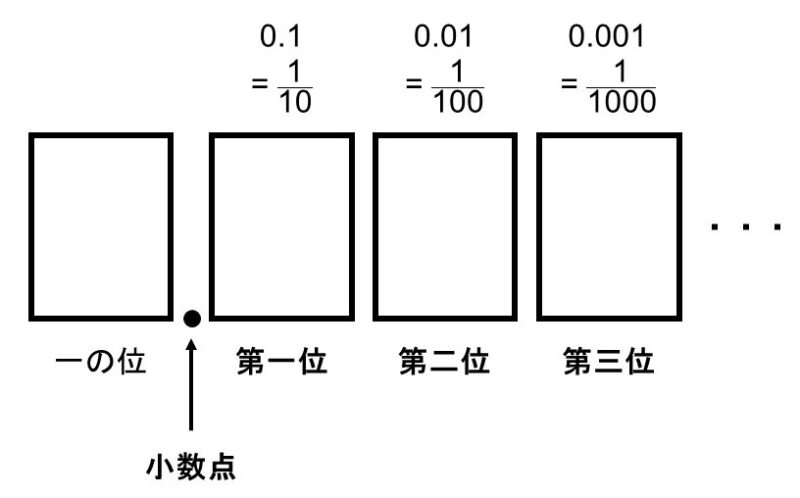
こうすることで、1を10個に分けたうちの一つが0.1($=\frac{1}{10}$)、0.1をさらに10個に分けたうちの一つが0.01($=\frac{1}{100}$)、…という具合で、より小さい数を考えることができます。
小数→分数にするには?
小数で表される数は分数に直すことができます。例として、1.25を分数にしてみましょう。
まず、1.25を位ごとの足し算に分解します。
$1.25 = 1+0.2+0.05$
0.2は$0.1 = \frac{1}{10}$が2個、0.05は$0.01 = \frac{1}{100}$が5個集まったものなので、この等式は
$1.25 = 1+\dfrac{2}{10}+\dfrac{5}{100}$
と書くこともできます。
これを通分して足し合わせれば分数になります。分母を100にそろえれば計算できますね。
$\begin{align}
1.25 & = 1+\dfrac{2}{10}+\dfrac{5}{100} \\[1.5ex]
& = \dfrac{100}{100}+\dfrac{20}{100}+\dfrac{5}{100} \\[1.5ex]
& = \dfrac{100+20+5}{100} \\[1.5ex]
& = \dfrac{125}{100} \\[1.5ex]
& = \dfrac{5}{4}
\end{align}$
約分まで行うと$\frac{5}{4}$となります。
分数→小数にするには?
続いて分数を小数に直す方法を見ていきましょう。これは割り算の筆算をベースにして考えることができます。
例として、先ほどの$\frac{5}{4}$を1.25に直してみましょう。
$\dfrac{5}{4} = 5 \div 4$
なので、これで割り算の筆算を組みます。

まずは一の位に1が立てることができ、引き算を行うと余りは1になります。ここまでは今までと同じです。
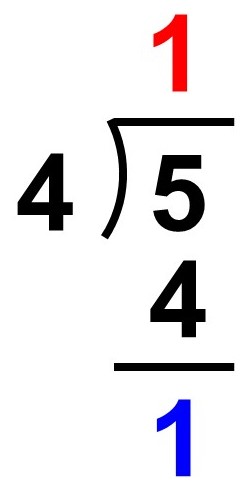
小数を考える場合は、ここからさらに割り算を行っていきます。ポイントは小数点以下(5の後ろ)に0が控えていると考えることです。この0は小数点第1位の0ですね。こう考えることで、余りである1の隣に0を下ろすことができます。
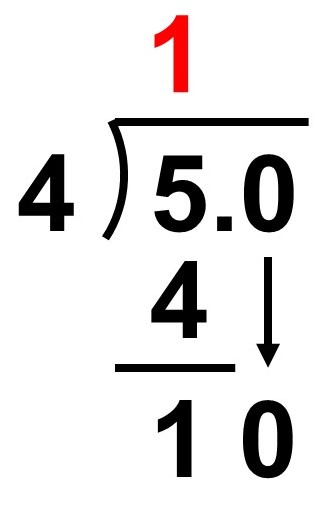
すると$10 \div 4 = 2\hspace{2pt}\text{…}\hspace{2pt}2$なので、次のようになりますね。

さらに割り算を進めます。小数点第2位に0があると見て、余りである2の隣に下ろします。
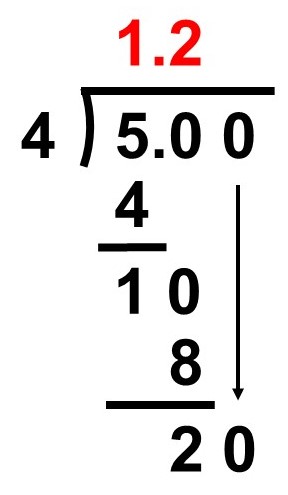
$20 \div 4 = 5$となるので、今度は割り切れました。
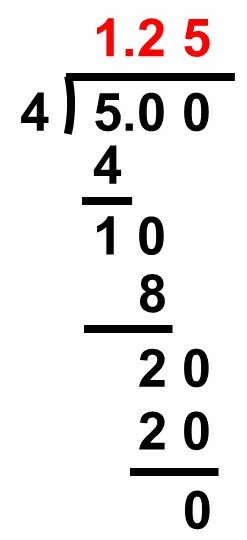
よって、
$\dfrac{5}{4} = 5 \div 4 = 1.25$
となります。
このように分数を小数に直す時は、小数点以下に0が続いていると見て、割り切れるまで筆算を行います。
分数と小数の使い分け
では、分数と小数はどうやって使い分ければよいのでしょうか?
まず分数のメリットですが、これは「あらゆる場面で数として表せる」ことです。前回お話しした「分数の使い方」にもつながりますが、表したい数が割り算で求まるのであれば、それをそのまま分数として表すことができます。
一方、小数のメリットとしては「一目で数の大きさがわかる」ことが挙げられます。これは10進法が使われているからですね。
例えば、2つの数が並んでいる時、大小を比べるのであれば小数の方がすぐにわかります。
- $\dfrac{5}{4}$ と $\dfrac{61}{50}$
- 1.25 と 1.26
この両者はどちらも同じ数を並べたものですが、10進法に慣れている皆さんであれば、間違いなく下の方が大小の見分けがつくかと思います。このようなメリットから、日常生活では小数を用いられることが多いです。
ただ、計算は小数よりも分数の方がやりやすいです。小数の計算についてはこれから学んでいきますが、基本的に桁数が多くなるので筆算を使う必要が出てきます。
一方で同じ数を表す場合、分数の方が形はシンプルになることが多い(1.25と$\dfrac{5}{4}$が良い例)上に、約分も使えるので計算がしやすいです。
これらを踏まえると、数式として問題を処理したい時は分数、人に数字を示したりする時は小数を使うのがベストですね。
【分数】
- あらゆる場面で数として表せる
- 数の大きさは比べにくい(通分が必要)
- 計算はしやすい(約分が使える)
⇒ 数式処理に便利!
【小数】
- 一目で数の大きさがわかる(10進法のおかげ)
- 計算はしにくい(桁数が増えがち)
⇒ 人に数字を示すのに便利!
まとめ
今回は分数と小数の違いについて学びました。まとめると次のようになります。
- 小数では、一の位の後ろにも「桁(小数点第○位)」があると考える
- 小数→分数では、「位ごとに分解して分数の足し算とする」か「自然数に直すには何倍する必要があるかを考える」
- 分数→小数では、割り算の筆算を使う
- 分数のメリットは「あらゆる場面で数として表せる」こと、小数のメリットは「一目で数の大きさがわかる」こと
分数と小数はどちらも便利ですが、やはりメリット・デメリットがあるので、それを理解した上で使い分けましょう!
今回はここまでです。お疲れさまでした!