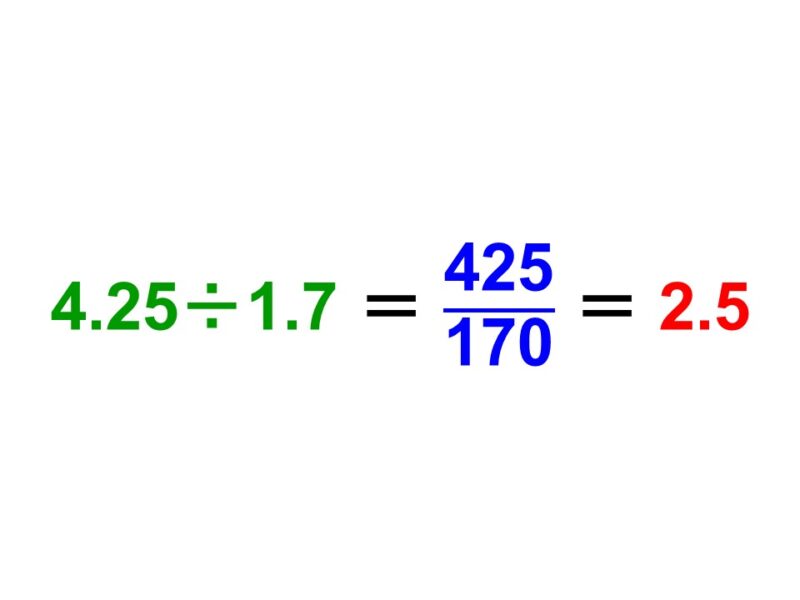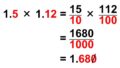こんにちは、まてがめです。
ここまで「分数」と「小数」について学んできました。この2つは表し方こそ違いますが、どちらも0や自然数(1, 2, 3, …)の間に存在する数を表せるという点では本質的に同じです。したがって、状況に応じて使い分けていくことになります。
この階では分数と小数について、「その表し方・計算方法・どんな時に使えるのか」を整理していきます。しっかり復習していきましょう!
分数
分数とは?
分数は「ある数をある数だけ等しく分けた時の1つ分」を表します。分けられる数を分子、分ける数を分母と言い、次のように表します。
$\dfrac{\text{分子}}{\text{分母}}$
(例)
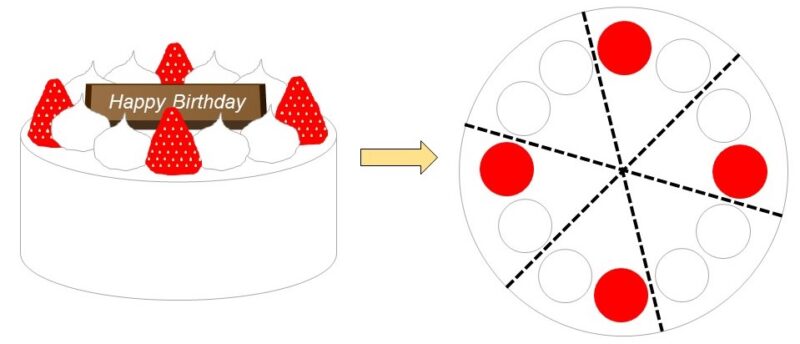
1個のケーキを6等分すると、1ピース分は
$\dfrac{1}{6}$個
そのため、分数は割り算と等しい関係にあります。
$1 \div 6 = \dfrac{1}{6}$
すなわち、割り算はそのまま分数として表すことができます。特に割り算において、割られる数が割る数よりも小さい(分子よりも分母が大きい)場合や余りを表す必要がない(速さ・密度・濃度など)場合は分数を使うと便利です。
分数は「ある数をある数だけ等しく分けた時の1つ分」を表すと言いましたが、これは「ある数だけ等しく分けてできるまとまりが何個分あるか」を表しているとも言えます。このような考え方が割合や比率に対応しています。
(例)
320人の生徒に国語、数学、英語、理科、社会の中で好きな教科についてアンケートをとり、百分率のグラフを作ると次のような結果となった。
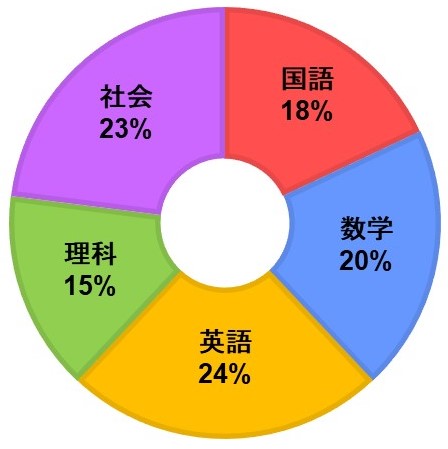
数学が好きな人の割合は
$\dfrac{20}{100} = \dfrac{1}{5}$
また、理科が好きな人の人数は
$320 \times \dfrac{15}{100} = 48$人
※約分、掛け算については後ほど解説します。
詳しい解説はこちら↓
分数の約分・通分
分数には「分母・分子に同じ数を掛けてもよい」、「分母・分子を同じ数で割ってもよい」という性質があり、これにより約分・通分という操作ができます。
約分
約分は、分数をより簡単な形にする(分母・分子をより小さい数にする)操作です。効率よく計算したり、得られた計算結果を答えとして書いたりする時によく使います。
(例)
$\begin{align}
\dfrac{12}{18} & = \dfrac{2 \times 2 \times 3}{2 \times 3 \times 3} \\[1.5ex]
& = \dfrac{(2 \times 2 \times 3) \div 6}{(2 \times 3 \times 3) \div 6} \\[1.5ex]
& = \dfrac{2}{3}
\end{align}$
例のように必要に応じて素因数分解(数を素数の積で表す操作)を行うと、分母・分子に共通する因数がわかりやすくなり、約分しやすくなります。
また、慣れてきたら分母・分子を共通因数で割る操作は次のように省略してもよいです。
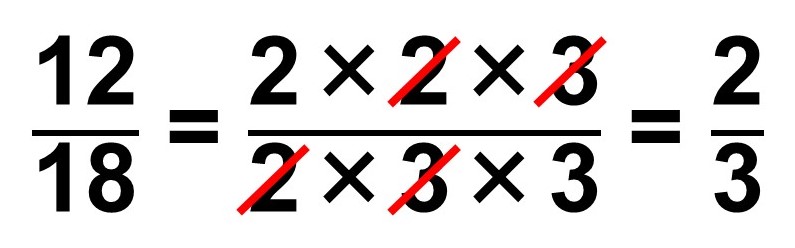
通分
通分は、複数の分数において分母をそろえる操作です。分数同士で大小を比べたり、足し算や引き算を行ったりする時によく使います。
(例)
$\dfrac{7}{10}$と$\dfrac{11}{15}$の大小を考えると、
$\begin{align}
\dfrac{7}{10} & = \dfrac{7}{2 \times 5} \\[1.5ex]
&=\dfrac{7 \times 3}{(2 \times 5) \times 3} \\[1.5ex]
& = \dfrac{21}{30}
\end{align}$
$\begin{align}
\dfrac{11}{15} & = \dfrac{11}{3 \times 5} \\[1.5ex]
& = \dfrac{11 \times 2}{(3 \times 5) \times 2} \\[1.5ex]
& = \dfrac{22}{30}
\end{align}$
$\dfrac{21}{30}$よりも$\dfrac{22}{30}$の方が大きい。
つまり、$\dfrac{7}{10}$よりも$\dfrac{11}{15}$の方が大きい。
詳しくはこちら↓
分数の足し算・引き算
分数の足し算・引き算は通分を用いることで計算できます。通分による計算は、分配法則を使っていることに他なりません。
(例1)
$\begin{align}
\dfrac{2}{7}+\dfrac{3}{7} & = \dfrac{2+3}{7} \\[1.5ex]
& = \dfrac{5}{7}
\end{align}$
cf.) この計算を割り算で表すと、分配法則を使っていることがよくわかります。
$\begin{align}
\dfrac{2}{7}+\dfrac{3}{7} & = 2 \div 7+3 \div 7 \\[1.5ex]
& = (2+3) \div 7 \\[1.5ex]
& = 5 \div 7 = \dfrac{5}{7}
\end{align}$
(例2)
$\begin{align}
\dfrac{5}{6}-\dfrac{3}{8} & = \dfrac{5 \times 4}{(2 \times 3) \times 4}-\dfrac{3 \times 3}{(2 \times 4) \times 3} \\[1.5ex]
& = \dfrac{20}{24}-\dfrac{9}{24} \\[1.5ex]
& = \dfrac{20-9}{24} \\[1.5ex]
& = \dfrac{11}{24}
\end{align}$
詳しくはこちら↓
分数の掛け算・割り算
分数の掛け算は分母同士、分子同士の掛け算として計算することができます。必要に応じて約分を使いながら計算しましょう。
(例)
$\begin{align}
\dfrac{10}{33} \times \dfrac{11}{5} & = \dfrac{10 \times 11}{33 \times 5} \\[1.5ex]
& = \dfrac{2 \times 5 \times 11}{3 \times 11 \times 5} \\[1.5ex]
& = \dfrac{2}{3}
\end{align}$
分数の割り算は割る数の逆数(分母・分子を入れかえた分数)を掛けることで計算できます。この操作は、割り算を分数の形にした後で分母を1にする操作に由来します。
(例)
$\begin{align}
& \hspace{13pt} \dfrac{5}{7} \div \dfrac{3}{2} \\[1.5ex]
& = \dfrac{\dfrac{5}{7}}{\dfrac{3}{2}} = \dfrac{\dfrac{5}{7} \times \dfrac{2}{3}}{\dfrac{3}{2} \times \dfrac{2}{3}} \\[1.5ex]
& = \dfrac{5}{7} \times \dfrac{2}{3} \\[1.5ex]
& = \dfrac{10}{21}
\end{align}$
詳しくはこちら↓
小数
小数とは?
「一の位の下にも位がある」と考えて、1より小さい数についても10進法と位取りを使って数えられるようにします。これが小数です。
小数を使う場合は小数点を境として、一の位の右隣に小数点第1位($\dfrac{1}{10}$の位)、小数点第2位($\dfrac{1}{100}$の位)、…と位が続いていきます。
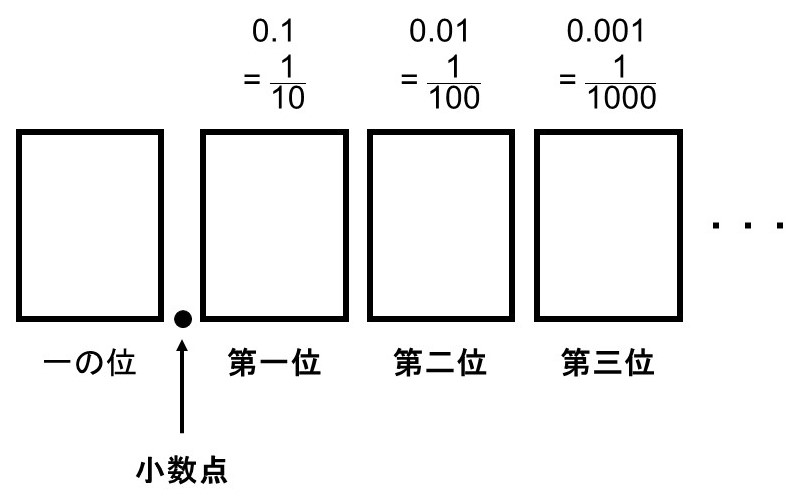
分数よりも表し方が自然数の時と似ているため、一目見た時の数の大きさがイメージしやすいです。したがって、人に数を示したい時などに便利です。一方で、表した時の桁数はどうしても多くなってしまうため、計算は分数よりもやりにくい場合が多いです。
小数は次のようにして分数に変換することができます。
(例)
$\begin{align}
2.57 & = 2+\dfrac{5}{10}+\dfrac{7}{100} \\[1.5ex]
& = \dfrac{200}{100}+\dfrac{50}{100}+\dfrac{7}{100} \\[1.5ex]
& = \dfrac{257}{100}
\end{align}$
逆に分数を小数に変換する場合、分数を割り算にして計算します。この時、余りがなくなるまで割り算を行います。
(例)
$\dfrac{7}{4} = 1.75$
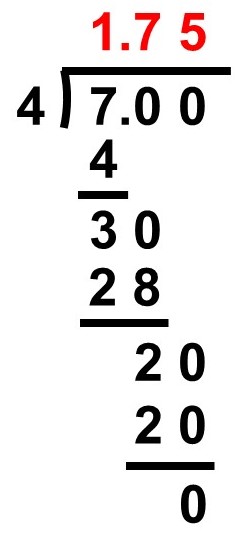
詳しくはこちら↓
小数の四則演算(加減乗除)
小数は10進法と位取りを基にしているため、基本的な計算方法は自然数の時とほぼ同じです。ただし、掛け算と割り算については小数点の位置に気をつけましょう。
小数の足し算・引き算
自然数の時と同じく、位をそろえて計算します。
(例1)
$3.28+2.57 = 5.85$

(例2)
$1.378-0.659 = 0.719$

小数の掛け算
分数に直してから(分子で)計算を行い、最後に小数に戻します。こうすることで、計算を自然数の時と同じように行いつつ、小数点の位置を正しく決めることができます。
(例)
$\begin{align}
0.28 \times 0.4 & = \dfrac{28}{100} \times \dfrac{4}{10} \\[1.5ex]
& = \dfrac{28 \times 4}{100 \times 10} \\[1.5ex]
& = \dfrac{112}{1000} \\[1.5ex]
& = 0.112
\end{align}$
小数の割り算
分数に直してから分母・分子が自然数となるよう同じ数を掛けることで、通常の分数(割り算)として計算することができます。
(例)
$\begin{align}
4.25 \div 1.7 & = \dfrac{4.25}{1.7} \\[1.5ex]
& = \dfrac{4.25 \times 100}{1.7 \times 100} \\[1.5ex]
& = \dfrac{425}{170} \\[1.5ex]
& = 425 \div 170 \\[1.5ex]
& = 2.5
\end{align}$
詳しくはこちら↓
トピック 割り算で÷0ができない理由
分数・小数がわかるようになると、割り算で「÷0が定義できない」理由もわかるようになります。
割り算=分数ですから、分数で分母をどんどん小さい数にしていけば÷0の答えがわかりそうですね。試しに$\frac{1}{\text{○}}$で分母を小さくしていってみましょう。
$\begin{align}
\dfrac{1}{10} & = 0.1 \\[1.5ex]
\dfrac{1}{1} & = 1 \\[1.5ex]
\dfrac{1}{0.1} & = 10 \\[1.5ex]
\dfrac{1}{0.01} & = 100 \\[1.5ex]
\dfrac{1}{0.001} & = 1000 \\[1.5ex]
\dfrac{1}{0.0001} & = 10000
\end{align}$
…
このように分母を小さくしていくと限りなく答えは大きくなっていくことがわかります。これを数学では「(正の無限大に)発散する」と言います。
つまり、0で割った時の答えというのは限りなく大きい(無限大)ので、限りある数を使って○○と答えることはできないというわけですね。
まとめ
分数や小数は「数に対する考え方」を広げるための第1歩です。これらがわかるようになると、自然数(1, 2, 3, …)だけではカバーしきれなかった数や量を表したり計算したりできるようになります。
今回のまとめと合わせ、実際に扱っていく中で分数・小数の意味や性質について深い理解を身につけていってくださいね。
今回はここまでです。また次の階でお会いしましょう!