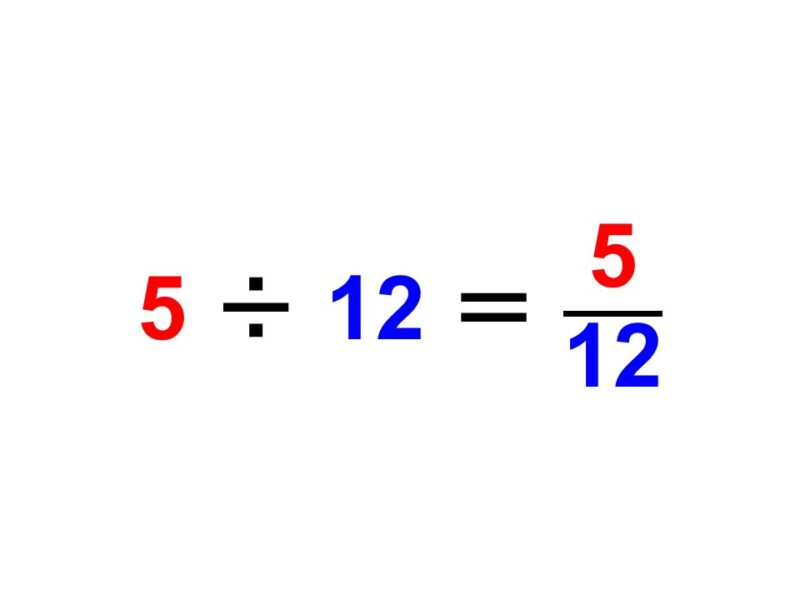こんにちは、まてがめです。
まず、この階まで上がってきたみなさんは素晴らしいです。
ここに至るまでの間に、数学の基礎となる10進法・位取り、四則演算について学んできているかと思いますが、それだけでも見える世界はずいぶんと変わっているはずです。
「数」という考え方があるということ、そしてそれを使って身の回りの物事を計算できるということは、できる人からすれば何とも思わないかもしれません。ですが、「目の前に存在しないもの(数)を頭の中で扱って、現実のことを理解したり解決したりする」って普通にすごいことだと思いませんか?
なので、それができるみなさんであれば、この先の内容も必ず理解していけると信じています。
さて今回からは、「数」についての考え方を広げることを試みます。その第一歩が分数(ぶんすう)と呼ばれるものです。
1より小さい数はどう数える?
次のような例を考えてみます。
今日は誕生日ということで、お母さんが自分のためにホールケーキを1個買ってきてくれた。今からこれを家族4人で分けて食べたい。
この時、1人分の量はどうなるか?
式を立てるとすると、割り算で表すことができそうです。
$1 \div 4$
ですが、ここで問題があります。これまでの割り算の考え方でいくと、これは計算できません。かといって、答えが0というのも変ですよね(「ケーキは食べられません」では誕生日に家族全員が泣いてしまいます…)。
こういう時は普通、図のようにケーキを切り分けてみんなで食べるはずです。
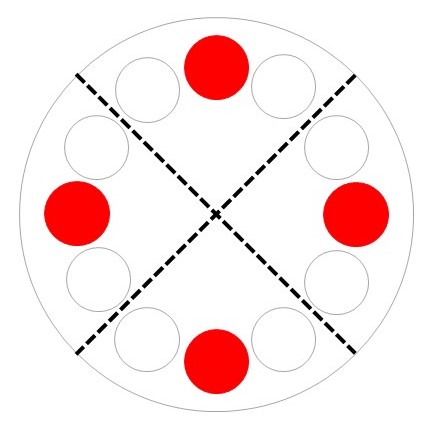
それでは、この切り分けた1人分は何と数えたらよいのでしょうか?1個よりも少ない量なので、これまでの数の数え方では限界があります。
そこで登場するのが分数(ぶんすう)です。分数を使うと、この1人分は次のように表せます。
$\frac{1}{4}$
4の部分(線の下側)を分母(ぶんぼ)と呼び、「いくつに分けるのか」を表します。一方、1の部分(線の上側)を分子(ぶんし)と呼び、「分けられる数」を表します。読み方は「4分の1」です。
よって、今回の答えは$\frac{1}{4}$個(4分の1個)となります。
ここで一番大切なポイントは、割り算を分数に対応させることができるという点です。すなわち、次のような等式が書けます。
$\text{分子} \div \text{分母} = \dfrac{\text{分子}}{\text{分母}}$
このように分数は1より小さいものを数えるのに便利です。もう一つ例を見てみましょう。
今、厚紙でできた箱を作るために、長さ5 mのテープを12等分して使いたい。
この時、使うテープの長さは何mになるか?
式にすると、
$5 \div 12$
となりますが、分数を使うことで
$5 \div 12 = \dfrac{5}{12}$
と表せます。つまり、$\frac{5}{12}$ mということですね。普通に割り算ができないので、これは1 m($= \frac{12}{12}$ m)よりも短い長さです。
このように、1よりも小さい分数(分母より分子が小さい分数)は真分数(しんぶんすう)と呼ばれることもあります。
1よりも大きい分数
分数には1よりも大きい数も表すことができます。次のような例で考えてみましょう。
Aさんは家から800 m離れた学校に行くのに、歩いて7分かかるという。
この時、Aさんは1分で何m歩いていることになるか?
いわゆる速さ(決められた時間の中でどのくらいの距離を進むのか)を求める問題ですね。
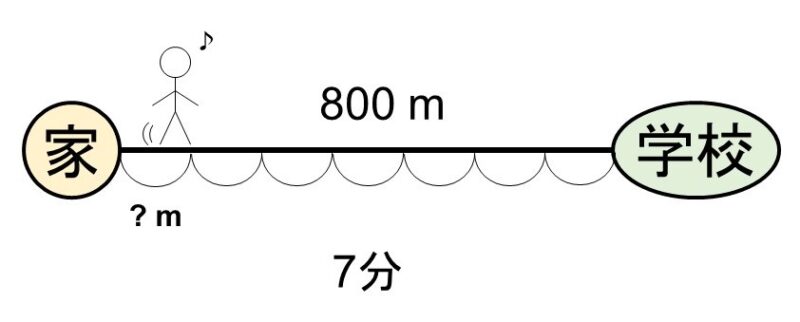
1分でどのくらい進むのかを考えるので、式は次のようになります。
$800 \div 7$
これは普通に割り算ができそうです。とりあえず計算してみると、
$800 \div 7 = 114 \hspace{2pt} \text{…} \hspace{2pt} 2$
計算はできましたが余りも出てしまいました。これはどう理解すればよいでしょうか?結果を基にして一度掛け算の形に直してみます。
$114 \times 7 + 2 = 800$
ここから言えるのは、「114 mで7分進んだ分と2 mを合わせると800 mになる」ということです。つまり残り2 m足りないので、1分で進む距離は114 mではありません。
ここで分数が使えます。分数の場合、割り算の式をそのまま表した形で書くことができるからです。余りを気にする必要すらありません。
$800 \div 7 = \dfrac{800}{7}$
よって、答えは$\frac{800}{7}$ mです。
このように1よりも大きな数も分数で表すこともあります。こうした分数(分母よりも分子が大きい分数)は仮分数(かぶんすう)と呼ばれます。
ちなみに、先ほどの割り算の結果を上手く使う方法もあります。すなわち、800 mを7で割った結果、残り2 mだけ余ったので、分数を使ってこれも7で割ってしまえばよいと考えれば、計算結果は
$114 + \dfrac{2}{7}$
であるとも言えます。しかしこれだと+が残っていますよね?そこで、帯分数(たいぶんすう)と呼ばれる表現を使います。
$800 \div 7 = 114\dfrac{2}{7}$
今までの割り算も活かしつつ分数も使った、いいとこ取りの表現です。実際、答えが114 m+αだというのが一目でわかりますね。必要に応じて使うのがよいでしょう。
分数による数の考え方の拡張
ちょうどよい機会ですので、私たちの頭の中にある「数に対する考え方」をここで一度整理しておきましょう。
まず、私たちは最初に「数」について学んだことで、次のような数直線が頭の中にできました。
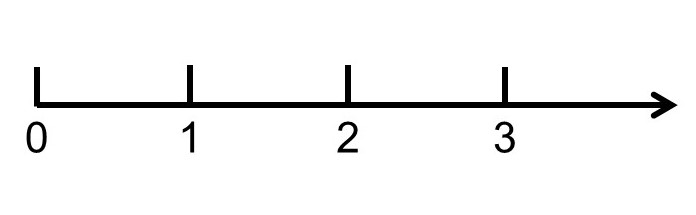
0から始まって、1, 2, 3, …と1ずつ増えながら続いていくようなイメージです。
ちなみに、1から順に1ずつ増えながら続いていく数のことを自然数(しぜんすう)と呼びます(0は含みません)。私たちがモノを数えたりするのによく使う数のことですね。
ただ今回、自然数に加えて新たに分数という数の考え方を知ったことによって、私たちの頭の中の数直線には新しい目盛りができました。
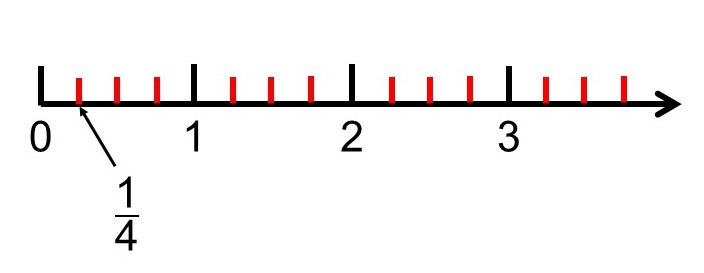
分数という「虫眼鏡」を手に入れたことで、「今まで目に見えていなかった小さな数も見えるようになった」と言えますね。
これからこの数直線がどうなっていくのか楽しみですね。
まとめ
今回は数に対する新しい考え方として分数を学びました。まとめると次の通りです。
- 全ての割り算は「分数」という形で表すことができる
- 分数を使うことで1より小さい数を(真分数として)表せる
- 分数を使うことで1より大きい数も余りを気にせずに(仮分数・帯分数として)表せる
- 分数によって、数の考え方に新しい広がりが生まれる
今回特に大切なことは、「割り算と分数は同じものである」ということです。つまり、分数はそれ自体が「数」を表しながらも「割り算」も表しているので、必要に応じてどちらにも捉えることができる非常に便利な数です(これが二刀流というやつか…!)。
分数はこれからどんどん使っていくので、使いながら扱いに慣れていきましょう!
今回はここまでです。お疲れさまでした!