今回の問題はこちらです。(※25Fまでの内容を理解していることが前提です!)
ある会社では特別な方法で作った砂糖を売っており、最近少しずつ人気が出てきた。その一方、作り方が難しいこともあり、わずかに加工ミスが起こることもわかっている。
そこで工場では、出荷前に機械Mを使い、加工ミスによる異物が入っていないかを検査している。異物が入る確率は$\frac{1}{20}$であるのに対し、機械Mが異物の有無を正しく判別できる確率は$\frac{97}{100}$であるという。
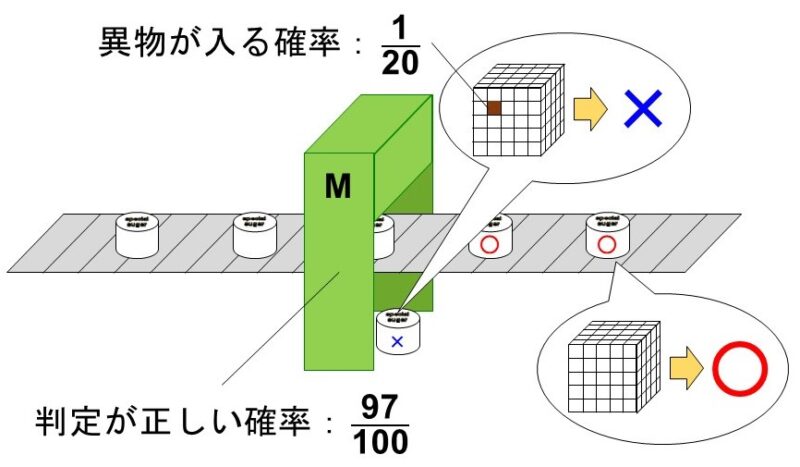
(1) 機械Mを使って製品の1つを検査したところ、『異物なし』の判定だった。この時、この製品に異物が入っている確率はいくらか?
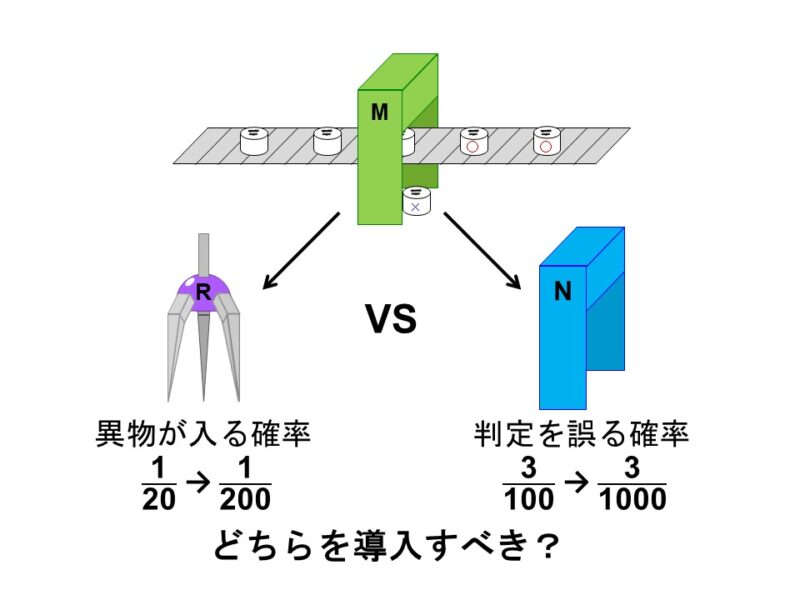
(2) 工場長としては「異物の入った製品が出荷される可能性をもっと減らしたい」と考えている。そこで、2つの案を用意した。
- 機械Mに加えて、異物を取り除く機械Rを導入する:
異物が入る確率を$\frac{1}{10}$にできる。 - 機械Mに代わって、新型の機械Nを導入する:
判別を誤る確率を$\frac{1}{10}$にできる。
この場合、どちらの案を採用するべきか?
(1) 検査の結果がわかっているということは…
まずは内容を整理しておきましょう。確率については次のことがわかっています。ちなみに確率の合計は必ず1なので、反対の事象の確率もわかります。
異物が入る確率:$\dfrac{1}{20}$
異物が入らない確率:$\dfrac{19}{20}$
機械Mが正しい確率:$\dfrac{97}{100}$
機械Mが誤る確率:$\dfrac{3}{100}$
ここで、
- $A$:異物が入っていない(⇔ $A^c$:異物が入っている)
- $B$:『異物なし』の判定が出る(⇔ $B^c$:『異物あり』の判定が出る)
とすると、起こりうる結果を次のような表としてまとめることができます。
| $A$ (異物が入っていない) | $A^c$ (異物が入っている) | |
| $B$ (『異物なし』の判定) | $A \cap B$ (異物が入っていない かつ 『異物なし』の判定) …正しい判定 | $A^c \cap B$ (異物が入っている かつ 『異物なし』の判定) …誤った判定 |
| $B^c$ (『異物あり』の判定) | $A \cap B^c$ (異物が入っていない かつ 『異物あり』の判定) …誤った判定 | $A^c \cap B^c$ (異物が入っている かつ 『異物あり』の判定) …正しい判定 |
それぞれの確率はどうなるでしょうか?試しに$P(A \cap B)$を計算してみましょう。
異物が入っていない確率は$\frac{19}{20}$です。一方、『異物なし』の判定が出る確率はというと、機械Mが正しい判定を行えばよいので、$\frac{97}{100}$だと考えられます。
また、「異物の有無」と「機械Mの判定」は独立な事象(異物の有無でMの能力が変わることはない)ですから、
$P(A \cap B) = \dfrac{19}{20} \times \dfrac{97}{100} = \dfrac{1843}{2000}$
となります。
同じようにして、それぞれの確率を計算すると次のようになります。
$P(A^c \cap B) = \dfrac{1}{20} \times \dfrac{3}{100} = \dfrac{3}{2000}$
$P(A \cap B^c) = \dfrac{19}{20} \times \dfrac{3}{100} = \dfrac{57}{2000}$
$P(A^c \cap B^c) = \dfrac{1}{20} \times \dfrac{97}{100} = \dfrac{97}{2000}$
(1)では、検査結果が『異物なし』とわかっている上で、実際に異物が入っている確率を計算したいので、条件付き確率$P_{B}(A^c)$を考えることになります。すなわち、求める確率は
$P_{B}(A^c) = \dfrac{P(A^c \cap B)}{P(B)}$
と表せます。
確率$P(B)$ですが、『異物なし』の判定となるのは$A \cap B$(異物が入っていない かつ 『異物なし』の判定)と$A^c \cap B$(異物が入っている かつ 『異物なし』の判定)の2通りです。そしてこれらは排反な事象ですから、
$P(B) = P(A \cap B) + P(A^c \cap B)$
と書けます。よって、
$\begin{align}
P(B) & = P(A \cap B) + P(A^c \cap B) \\[1.5ex]
& = \dfrac{1843}{2000} + \dfrac{3}{2000} \\[1.5ex]
& = \dfrac{1846}{2000}
\end{align}$
となります。
以上から、求める確率$P_{B}(A^c)$は
$\begin{align}
P_{B}(A^c) & = \dfrac{P(A^c \cap B)}{P(B)} \\[1.5ex]
& = \dfrac{\dfrac{3}{2000}}{\dfrac{1846}{2000}} \\[1.5ex]
& = \dfrac{3}{1846}
\end{align}$
となります。これは、およそ0.16%の確率で異物入りの製品が出荷されてしまう可能性があることを意味しています。
(2) 条件付き確率で比べてみよう
異物入りの製品が出荷される可能性を小さくするには、先ほど求めた「『異物なし』の判定が出た上で、その製品に実際に異物が入っている確率($P_{B}(A^c)$)」を小さくする必要があります(『異物なし』の判定が出てしまえば、後はそのまま出荷されてしまいますからね)。
では、2つの案についてそれぞれ考えてみましょう。
[1] 機械Mに加えて、異物を取り除く機械Rを導入する場合
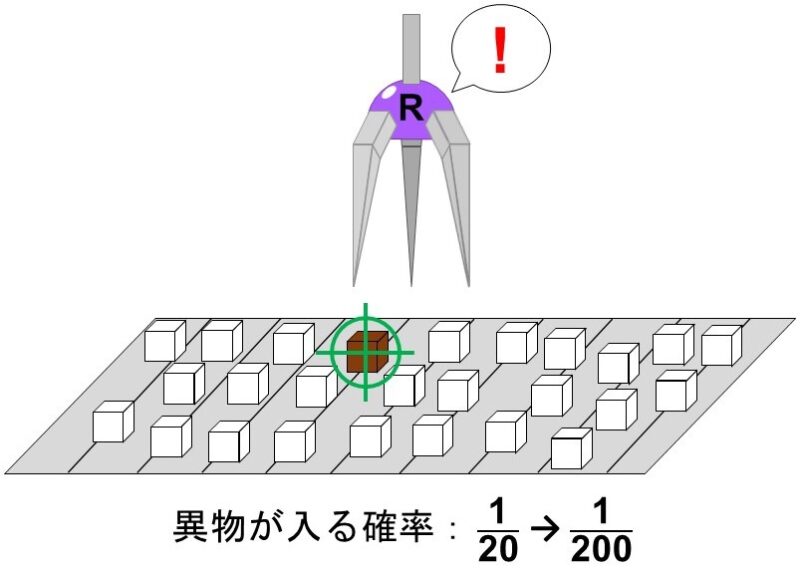
この場合、異物が入る確率が$\frac{1}{10}$になるので、
異物が入る確率:$\dfrac{1}{200}$
異物が入らない確率:$\dfrac{199}{200}$
となります。
一方、機械Mはそのまま使うので、(1)と同じです。
機械Mが正しい確率:$\dfrac{97}{100}$
機械Mが誤る確率:$\dfrac{3}{100}$
これらより、
$P(A \cap B) = \dfrac{199}{200} \times \dfrac{97}{100} = \dfrac{19303}{20000}$
$P(A^c \cap B) = \dfrac{1}{200} \times \dfrac{3}{100} = \dfrac{3}{20000}$
$\begin{align}
P(B) & = P(A \cap B) + P(A^c \cap B) \\[1.5ex]
& = \dfrac{19303}{20000} + \dfrac{3}{20000} \\[1.5ex]
& = \dfrac{19306}{20000}
\end{align}$
なので、求める確率は
$\begin{align}
P_{B}(A^c) & = \dfrac{P(A^c \cap B)}{P(B)} \\[1.5ex]
& = \dfrac{\dfrac{3}{20000}}{\dfrac{19306}{20000}} \\[1.5ex]
& = \dfrac{3}{19306}
\end{align}$
となります。百分率に直すと、およそ0.0155%です。
[2] 機械Mに代わって、新型の機械Nを導入する場合
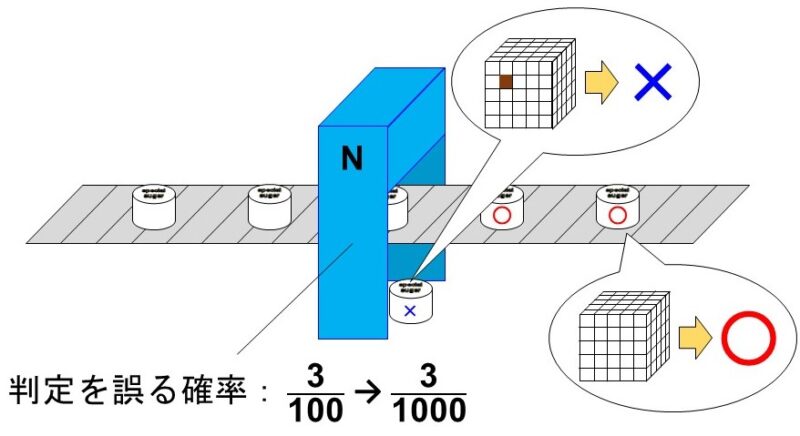
機械Nは機械Mに比べ、判別を誤る確率が$\frac{1}{10}$なので、
機械Nが正しい確率:$\dfrac{997}{1000}$
機械Nが誤る確率:$\dfrac{3}{1000}$
となります。
一方、異物が入る確率は変わらないので、(1)と同じです。
異物が入る確率:$\dfrac{1}{20}$
異物が入らない確率:$\dfrac{19}{20}$
これらより、
$P(A \cap B) = \dfrac{19}{20} \times \dfrac{997}{1000} = \dfrac{18943}{20000}$
$P(A^c \cap B) = \dfrac{1}{20} \times \dfrac{3}{1000} = \dfrac{3}{20000}$
$\begin{align}
P(B) & = P(A \cap B) + P(A^c \cap B) \\[1.5ex]
& = \dfrac{18943}{20000} + \dfrac{3}{20000} \\[1.5ex]
& = \dfrac{18946}{20000}
\end{align}$
なので、求める確率は
$\begin{align}
P_{B}(A^c) & = \dfrac{P(A^c \cap B)}{P(B)} \\[1.5ex]
& = \dfrac{\dfrac{3}{20000}}{\dfrac{18946}{20000}} \\[1.5ex]
& = \dfrac{3}{18946}
\end{align}$
となります。百分率に直すと、およそ0.0158%です。
よって、$P_{B}(A^c)$が小さいのは[1]の場合ですから、機械Rを導入する案を採用するべきということになります。
今回は、判定結果の原因が機械の誤りによるものである確率を条件付き確率として計算しました。このように、結果に対する原因について考える条件付き確率は「原因の確率」と呼ばれることがあります。
原因の確率は、今回のような検査などの場面で考えることができ、確率の応用例の一つとして知られています。