こんにちは、まてがめです。
前回は、平面図形におけるルールである「5つの公理」について説明しました。
今後は「公理」をベースにして、平面図形における性質(定理)を展開していくことになります。
さて、平面図形を学ぶ上で欠かせない概念が角度(かくど)です。「角度」は前回、公理について解説した際にすでに出てきていますが、この階でその扱い方を学んでいきます。
角度とは?
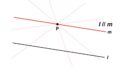
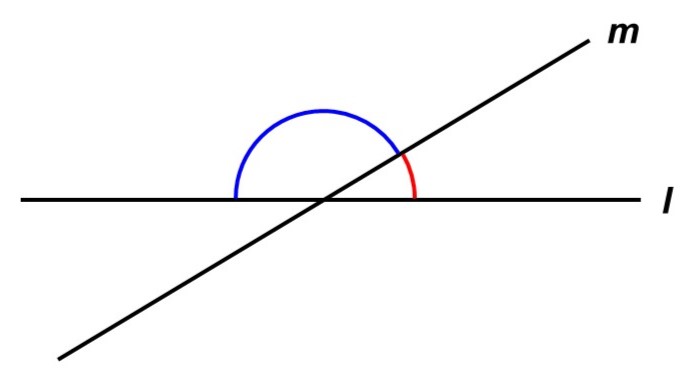
まずはおさらいです。角度は2本の線が交わる時、その交わり方を表す量(開き具合)として定義されます。例えば、直線$l$, $m$が図のように交わっている時、2種類の角度を考えることができます(4種類ではなく2種類である理由は後述)。
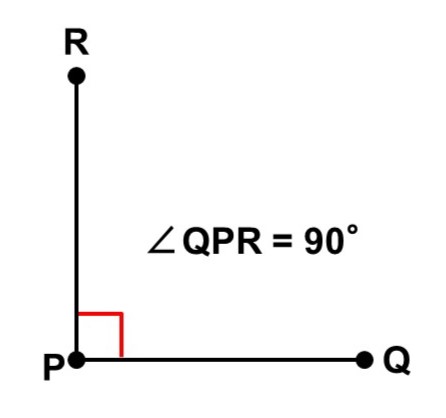
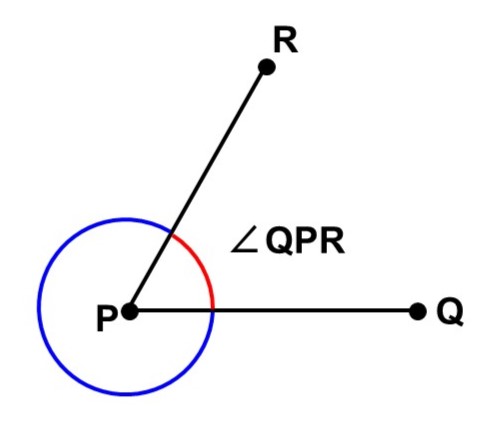
また、線分PQ, PRが図のように交わっている場合も2種類の角度を考えることができます。角度を表す時は$\angle \mathrm{QPR}$と書きますが、断りがない限り、これは小さい方の角度を表しているものとします。
なお、角度に記号を振る時は、ギリシャ文字(特に$\alpha$(アルファ), $\beta$(ベータ), $\theta$(シータ))がよく使われます。
角度を表すには?
「角度」という概念については、ある程度理解できたかと思います。そうなると当然、「角度の大きさをどう表したらよいか?」という疑問が生まれます。
角度を表す方法は一般に次の2種類があります。
度数法
こちらは1周を360°(360度)と決めて、角度の大きさを考える方法です。したがって、1周の$\frac{1}{360}$が1°になります。
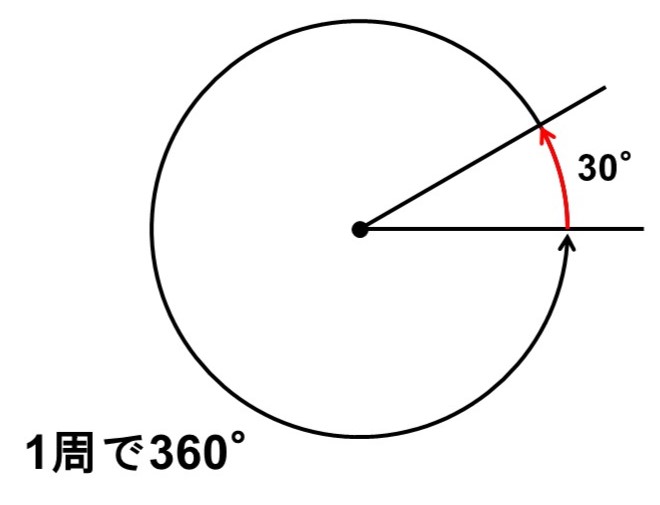
この方法のメリットは、「360」という数字にあります。360を素因数分解すると、
$360 = 2^3 \times 3^2 \times 5$
となります。ここから360が約数をいくつ持つのか計算してみます。約数を作るのに素数2, 3, 5をそれぞれ何個使うのか(2なら0~3個の4通り)を考えると、
$4 \times 3 \times 2 = 24$
すなわち、360という数字は24個の約数を持ちます。これだけ約数を持つということは、様々な角度を区切りのよい数で表すことができます。
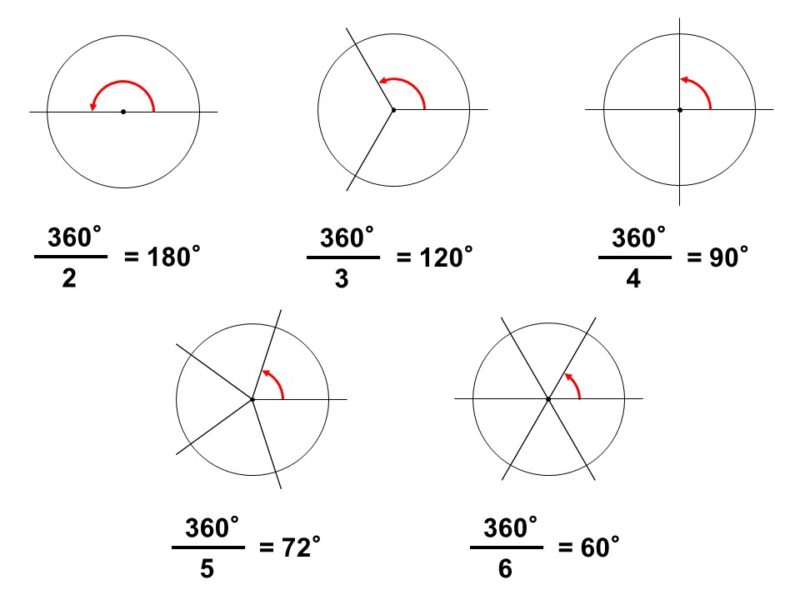
こうした利便性から、度数法は数学に限らず多くの分野で用いられています。この章でも、主に度数法を使って話を進めていきます。
弧度法
こちらは角度の大きさを「長さ」で考えます。すなわち、半径1の円周の長さを1周とします。
弧度法での単位は「ラジアン」といいます(実際には省略されることが多い)。長さ=角度として扱いますから、1ラジアン=長さ1ということになります。
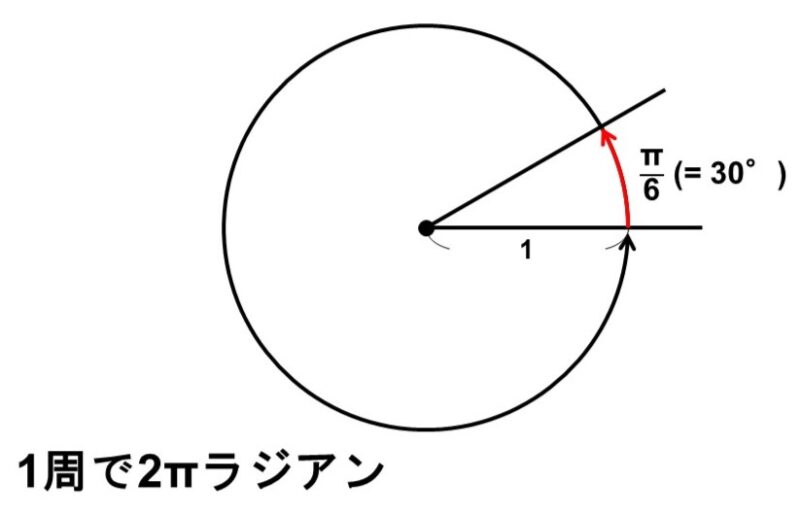
度数法では意図的に360という値を区切りとしましたが、弧度法ではいつも通り、10進法のまま角度を扱うことができるので、理学では一般的な方法として用いられています。
ただし先で述べたように、「円(周)」についてはこれから学んでいくので、しばらく弧度法は使わず度数法を使っていくことにします。
垂直と平行
角度の表し方を学んだところで、平面図形において重要な「垂直」と「平行」について考えていきます。
垂直
「垂直」とは、2本の直線が等しい角度をなして交わっている状態を指し、この時の角度を直角と呼びます。線分や半直線の場合も、両端を延ばしていった時に等しい角度で交われば「垂直」です。
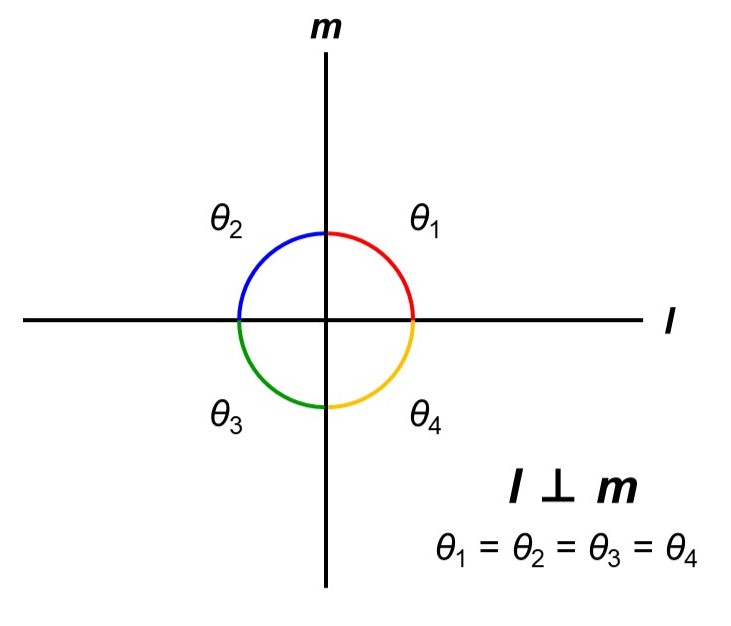
では、この時の角度(直角)を度数法で表してみましょう。1周分の角度360°がちょうど4等分されていますから、
$\dfrac{360^{\circ}}{4} = 90^{\circ}$
となります。逆に、角度が90 °ならば直角であり、2つの線は垂直に交わっていることになります。
- 「2本の線が垂直に交わる」⇒「角度は90°(直角)」
- 「角度が90°(直角)」⇒「2本の線が垂直に交わる」
平行
「平行」とは、2本の直線をどこまで延ばしても交わることがない状態を指します。線分や半直線の場合も、両端を延ばしていった時に交わらなければ「平行」であると言えます。
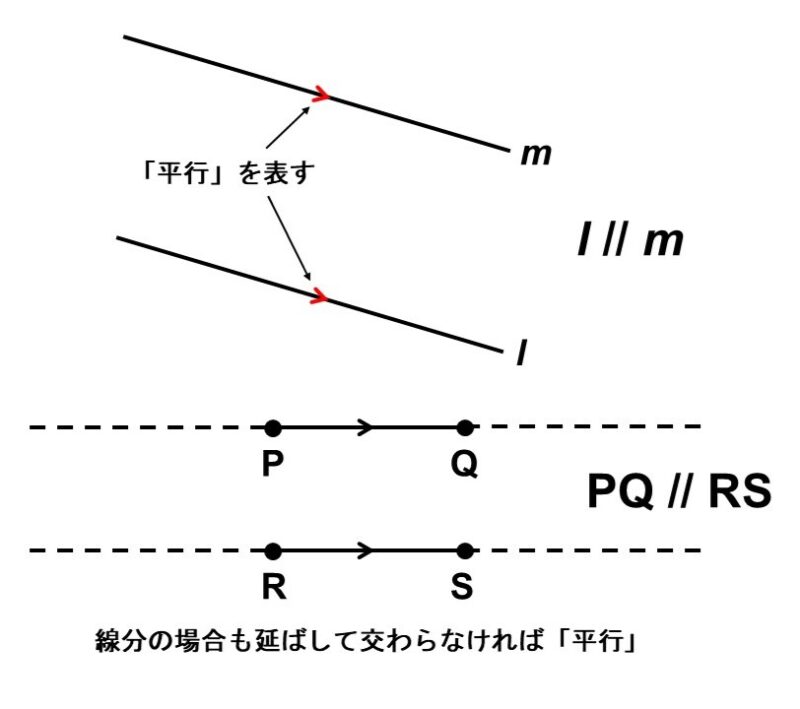
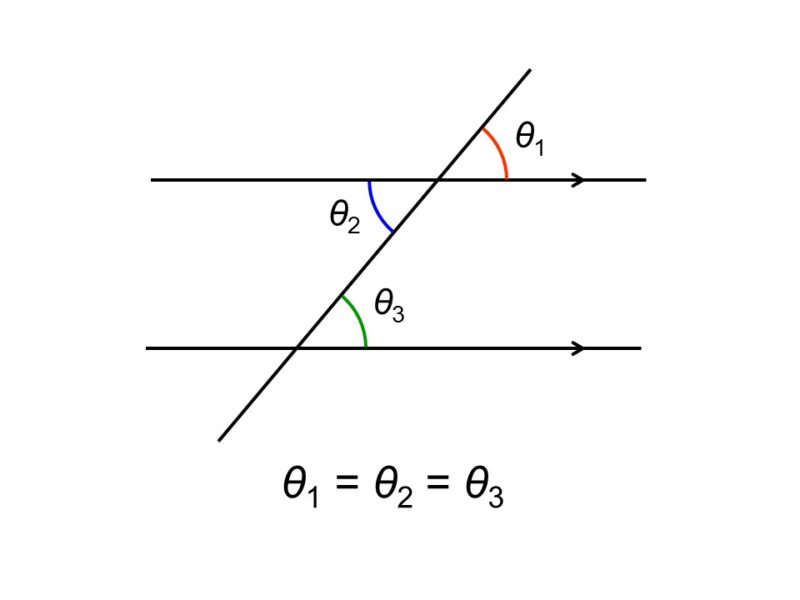
では、2本の線が平行な時、角度においてどんなことが言えるか考えてみましょう。平行な2本の直線$l$, $m$とこの2本の直線に交差する直線$n$を用意し、$m$と$n$のなす角を$\theta_{1}$, $\theta_{2}$, $\theta_{3}$, $\theta_{4}$とし、$l$と$n$のなす角を$\theta_{5}$, $\theta_{6}$, $\theta_{7}$, $\theta_{8}$とします。
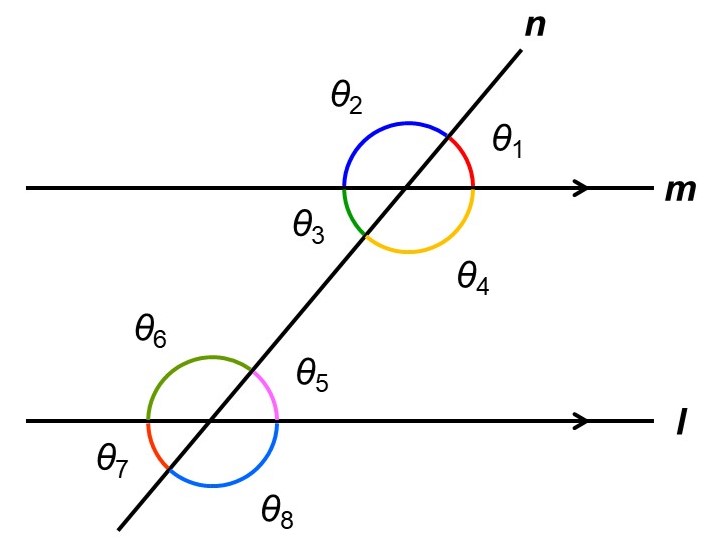
すると直線$n$から見て、直線$l$, $m$は同じ方向に延びているので、
$\theta_{1} = \theta_{5}$, $\theta_{2} = \theta_{6}$, $\theta_{3} = \theta_{7}$, $\theta_{4} = \theta_{8}$
であることがわかります。このような角度の組を同位角(どういかく)といいます。
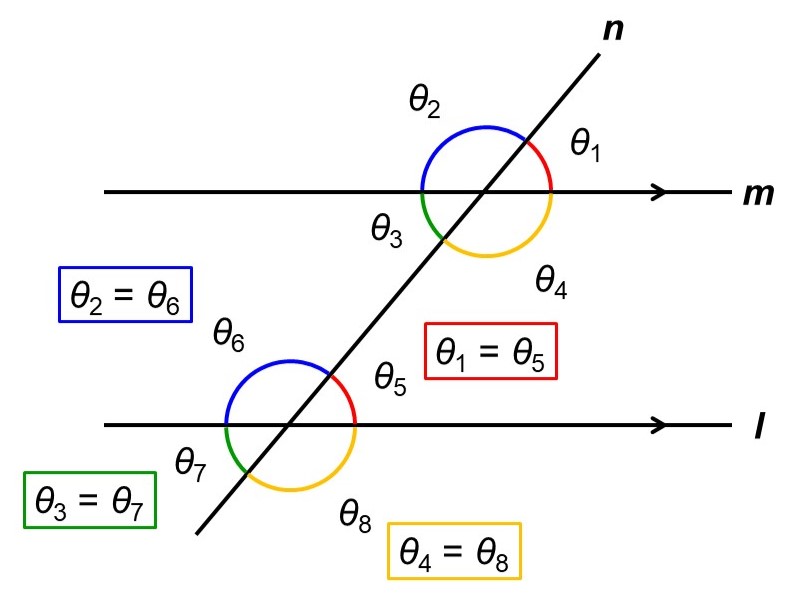
4組の同位角を示しましたが、等しい角度の組合せはさらにまとめることができます。
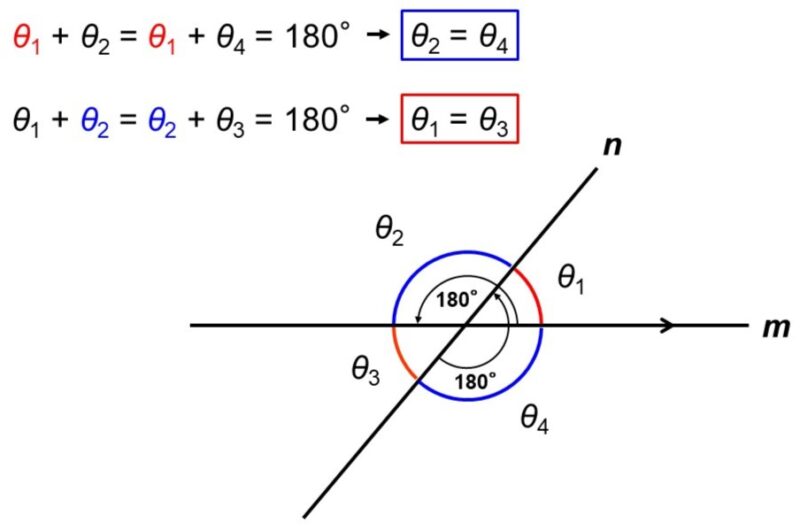
例えば、直線$m$と$n$のなす角に注目すると、
$\theta_{1}+\theta_{2} = \theta_{1}+\theta_{4} = \dfrac{360^{\circ}}{2} = 180^{\circ}$
となっているのがわかります(線上の角度は360°の半分の180°)。よって、$\theta_{2} = \theta_{4}$ということになります。
このような角度の組は、向かい合ったような状態になっていることから、対頂角(たいちょうかく)と呼ばれます。$\theta_{1}$と$\theta_{3}$も対頂角の組合せです。
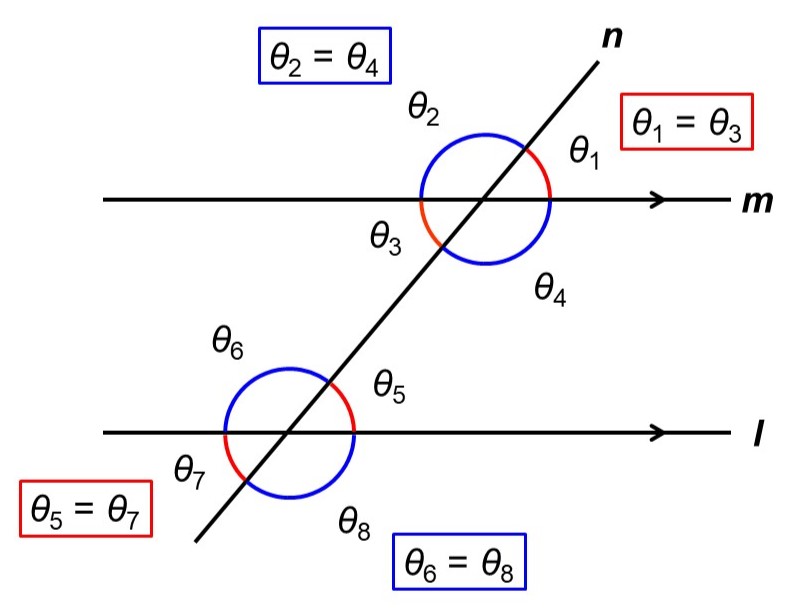
直線$l$と$n$のなす角においても対頂角を考えると、
$\theta_{5} = \theta_{7}$, $\theta_{6} = \theta_{8}$
なので、結果として等しい角度の組合せは2組にまとめることができます。
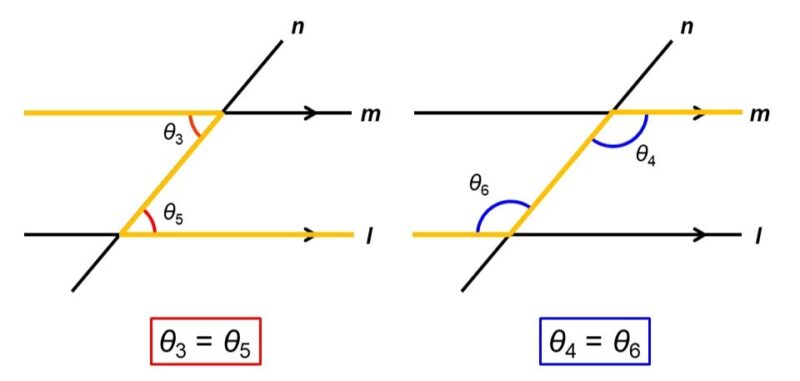
また、これにより次の角度もそれぞれ等しいことがわかります。
$\theta_{3} = \theta_{5}$, $\theta_{4} = \theta_{6}$
このような角度の組は錯角(さっかく)と呼ばれています。アルファベットのZ(もしくはその鏡文字)のような配置になっているのが特徴です。
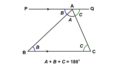
同位角・錯角は、「2本の線が平行か」を調べるために使うこともできます。例えば、次のような図形$\mathrm{ABCD}$があったとします。
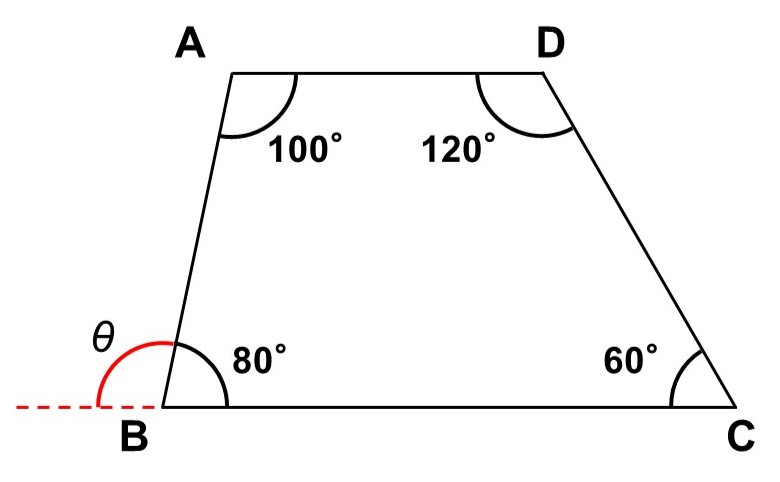
この時、線分$\mathrm{BC}$を延長して角度$\theta$の大きさを考えてみると、
$\theta = 180^{\circ}-80^{\circ} = 100^{\circ}$
となり、これは$\angle \mathrm{DAB}$と等しいので、錯角が等しいことになります。これより、$\mathrm{AD} /\!/ \mathrm{BC}$であることがわかります。
- 「2本の線が平行」⇒「同位角・錯角が等しい」
- 「同位角・錯角が等しい」⇒「2本の線が平行」
まとめ
今回は角度の扱い方について学びました。簡単にまとめると次のようになります。
- 角度:2本の線の交わり方(開き具合)を表す量
- 度数法:単位を「°(ど)」とし、1周を360°として角度を表す方法
- 弧度法:単位を「ラジアン」とし、1周を半径1の円周の長さ($2 \pi$ラジアン)として角度を表す方法
- 「2本の線が垂直に交わる」⇔「角度は90°(直角)」
- 「2本の線が平行」⇔「同位角・錯角が等しい」
「角度について理解する」ということが、そのまま「平面図形を理解する」ことにつながると言っても過言ではありません。
図形そのものを学んでいくのと同時に、角度の扱いにも少しずつ慣れていきましょう。
今回はここまでです。お疲れさまでした!