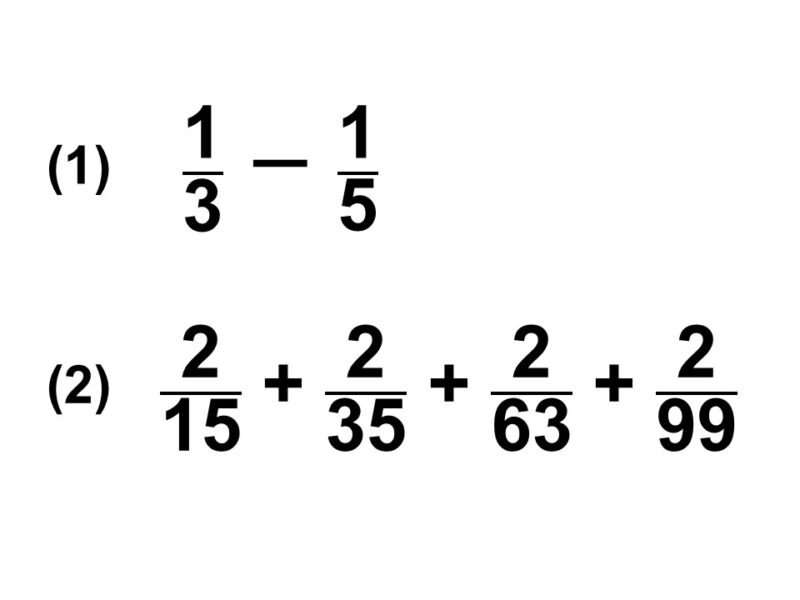今回の問題はこちらです。(※15Fまでの内容を理解していることが前提です!)
次の式を計算してください。
(1) $\dfrac{1}{3}-\dfrac{1}{5}$
(2) $\dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99}$
(1)はともかく、(2)が面倒そうです…さて、どうやって計算したらよいでしょうか?
(1)は基本に忠実でOK
(1)から計算してみましょう。分数の引き算なので、通分して分子同士で引き算を行います。分母の3と5はどちらも素数なので$3\times5=15$でそろえればよいですね。
$\begin{align}
\dfrac{1}{3}-\dfrac{1}{5}&=\dfrac{1 \times 5}{3 \times 5}-\dfrac{1 \times 3}{5 \times 3} \\[1.5ex]
& = \dfrac{5}{15}-\dfrac{3}{15} \\[1.5ex]
& = \dfrac{5-3}{15} \\[1.5ex]
& = \dfrac{2}{15}
\end{align}$
(2)もまずは基本に従って考えてみる
続いて(2)です。分数の足し算なので、最初に考えるのはもちろん通分ですよね。となれば、まずはそれぞれの分数の分母を素因数分解してみましょう。
$\begin{align}
& \hspace{13pt} \dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99} \\[1.5ex]
& = \dfrac{2}{3 \times 5}+\dfrac{2}{5 \times 7}+\dfrac{2}{3 \times 3 \times 7}+\dfrac{2}{3 \times 3 \times 11}
\end{align}$
復習ですが、通分は「各分母に足りないものを補う」イメージで行います。4つの分母を見た時、最低限必要な素数を拾い上げて掛け算にしてみると、
$3 \times 3 \times 5 \times 7 \times 11(= 3465)$
なので、これで分母をそろえれば良さそうです。
では通分した時に分子がどうなるか見てみます。通分する時は分母・分子に同じ数を掛けるので、分子には分母で不足していたものが来ることに気をつけましょう。
$\begin{align}
& \hspace{13pt} \text{(分子)} \\[1.5ex]
& = 2 \times 3 \times 7 \times 11+2 \times 3 \times 3 \times 11+2 \times 5 \times 11+2 \times 5 \times 7 \\[1.5ex]
& = 2 \times (3 \times 7 \times 11+3 \times 3 \times 11+5 \times 11+5 \times 7) \\[1.5ex]
& = 2 \times (231+99+55+35) \\[1.5ex]
& = 2 \times 420 \\[1.5ex]
& = 2 \times 2 \times 2 \times 3 \times 5 \times 7
\end{align}$
今回は分子で2が共通していたので、途中で分配法則を使い、2でくくっています。また、約分に備えて素因数分解まで行いました。
以上から、
$\begin{align}
& \hspace{13pt} \dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99} \\[1.5ex]
& = \dfrac{2 \times 2 \times 2 \times 3 \times 5 \times 7}{3 \times 3 \times 5 \times 7 \times 11} \\[1.5ex]
& = \dfrac{2 \times 2 \times 2}{3 \times 11} \\[1.5ex]
& = \dfrac{8}{33}
\end{align}$
となります。
ちょっと大変ではありますが、丁寧に計算すればできないこともありません。このくらいの分量をミスなく計算できると良いですね。
(1)は(2)のヒント?
…とはいっても、先ほどの計算量は決して少ないとは言えません。もっと楽をする方法は何かないでしょうか?
そう思いながら改めて(1)を見てみます。(1)によれば
$\dfrac{2}{15} = \dfrac{1}{3}-\dfrac{1}{5}$
ということでした。
したがって、(2)の式は次のように書くことができます。
$\begin{align}
& \hspace{13pt} \dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99} \\[1.5ex]
& = (\dfrac{1}{3}-\dfrac{1}{5})+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99}
\end{align}$
このままでは何もできませんが、もし同じようなことが残りの分数でもできるとしたらどうでしょうか?
試しに第2項の分数$\frac{2}{35}$を見てみましょう。$\frac{2}{15}$と比べてみると、分母を素因数分解して2つの数の積にした時、2つの数の差が分子と同じになるという点で共通しています。
$15 = 3 \times 5$ → $5-3 = 2$
$35 = 5 \times 7$ → $7-5 = 2$
となると、次が成り立ちそうだと予想できます。
$\dfrac{2}{35} = \dfrac{1}{5}-\dfrac{1}{7}$
実際に計算してみると、
$\begin{align}
\dfrac{1}{5}-\dfrac{1}{7} & = \dfrac{1 \times 7}{5 \times 7}-\dfrac{1 \times 5}{5 \times 7} \\[1.5ex]
& = \dfrac{7-5}{35} \\[1.5ex]
& = \dfrac{2}{35}
\end{align}$
となり、予想は正しいことがわかります。
この調子で残り2つの分数についても考えると、
$\dfrac{2}{63} = \dfrac{1}{7}-\dfrac{1}{9}$
$\dfrac{2}{99} = \dfrac{1}{9}-\dfrac{1}{11}$
とできることがわかるので、結局(2)の式は
$\begin{align}
& \hspace{13pt} \dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99} \\[1.5ex]
& = (\dfrac{1}{3}-\dfrac{1}{5})+(\dfrac{1}{5}-\dfrac{1}{7})+(\dfrac{1}{7}-\dfrac{1}{9})+(\dfrac{1}{9}-\dfrac{1}{11}) \\[1.5ex]
& = \dfrac{1}{3}-\dfrac{1}{11}
\end{align}$
とできます。内側で分数が打ち消し合うので、簡単な式になりました。したがって、
$\begin{align}
& \hspace{13pt} \dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99} \\[1.5ex]
& = \dfrac{1}{3}-\dfrac{1}{11} \\[1.5ex]
& = \dfrac{1 \times 11}{3 \times 11}-\dfrac{1 \times 3}{11 \times 3} \\[1.5ex]
& = \dfrac{11-3}{33} \\[1.5ex]
& = \dfrac{8}{33}
\end{align}$
となります。この解き方だと計算がシンプルなので、ミスなくすばやく計算できますね。
積分でも役立つ分数の分解 ― 部分分数分解
今回の問題で見たように、分母を2つの数の積で表した時、その差が分子と同じであれば、引き算を使って分数を分解することができます。
(例)
$\begin{align}
\dfrac{3}{130}&=\dfrac{3}{10 \times 13} \\[1.5ex]
& = \dfrac{1}{10}-\dfrac{1}{13}
\end{align}$
ちなみに分子がこの条件を満たさない場合でも、掛け算を使って調整すると同じような分解ができます。
(例)
$\begin{align}
\dfrac{5}{21} & = \dfrac{4}{3 \times 7} \times \dfrac{5}{4} \\[1.5ex]
& = (\dfrac{1}{3}-\dfrac{1}{7}) \times \dfrac{5}{4} \\[1.5ex]
& = \dfrac{5}{12}-\dfrac{5}{28}
\end{align}$
今回の問題ではこれを利用し、「内側の分数同士で打ち消し合って端の分数のみが残る」ようにしましたが、このような計算はその形から「キセル算」という名前で知られています。
ところでこの変形、実は高校数学の山場とも言える「積分」でも活躍します(まだ積分は扱っていませんので、今は「高度な数学にも使えるんだなあ」くらいに理解してもらえればOKです)。
最も簡単な分数関数
$\dfrac{1}{x}$
の不定積分は次のようになることが知られています。
$\displaystyle
\int \dfrac{1}{x}\,dx = \log |x|+C
$ ($C$は積分定数)
logは「対数」、$|x|$は「絶対値」という関数ですが、わからなくても大丈夫です。ここでは「$\frac{1}{x}$という関数に対しては公式を使って積分ができる」ということだけ理解してください。
一方、積分は関数同士の掛け算が入ってくると、とたんにこうした公式が使えなくなります。例えば、分数関数
$\dfrac{1}{x(x+1)}$
の不定積分を行う場合、分母に$x$と$x+1$の掛け算があるため、先ほどの公式をそのまま使うことができません(※文字式では掛け算の記号×は省略されます)。
このような時に分数の分解(部分分数分解)が使われます。すなわち、
$\dfrac{1}{x(x+1)}=\dfrac{1}{x}-\dfrac{1}{x+1}$
とすることで、次のようにして公式が使えるようになります。
$\begin{align}
\int \dfrac{1}{x(x+1)}\,dx & = \int (\dfrac{1}{x}-\dfrac{1}{x+1})\,dx \\[1.5ex]
& = \int \dfrac{1}{x}\,dx-\int \dfrac{1}{x+1}\,dx \\[1.5ex]
& = \log |x|-\log |x+1|+C \\[1.5ex]
& (=\log \left| \dfrac{x}{x+1} \right|+C)
\end{align}$ ($C$は積分定数)
分数の分解そのものは単純ですが、このように今後も使える場面は多いので、ぜひ覚えておきましょう!