こんにちは、まてがめです。
前回は、ある物事が未来で起こる可能性を表す量である「確率」について学びました。
この階でお話ししたように、確率を求める時は、場合の数を調べて「割合」という形で分数に表すのが基本です。しかし、これがわかるだけでは、確率を本当に理解したとはまだ言えません。
実は、確率には大切な特性があります。それは「四則演算ができる」ことです(もちろん「確率は数で表せるから四則演算ができる」ということが言いたいわけではないです)。ここで言う「四則演算ができる」とは、「確率同士の足し算・引き算・掛け算・割り算にはちゃんとした意味がある」ということです。ここまで理解して、初めて確率がわかるようになったと言えます。
今回は「どんな時に確率の四則演算ができるのか」や「確率の四則演算にどんな意味があるのか」について学んでいきます!
確率の足し算・引き算 ― 排反と余事象
まずは、確率の足し算・引き算について解説します。これは、確率の表し方と集合を考えることでその意味がわかります。
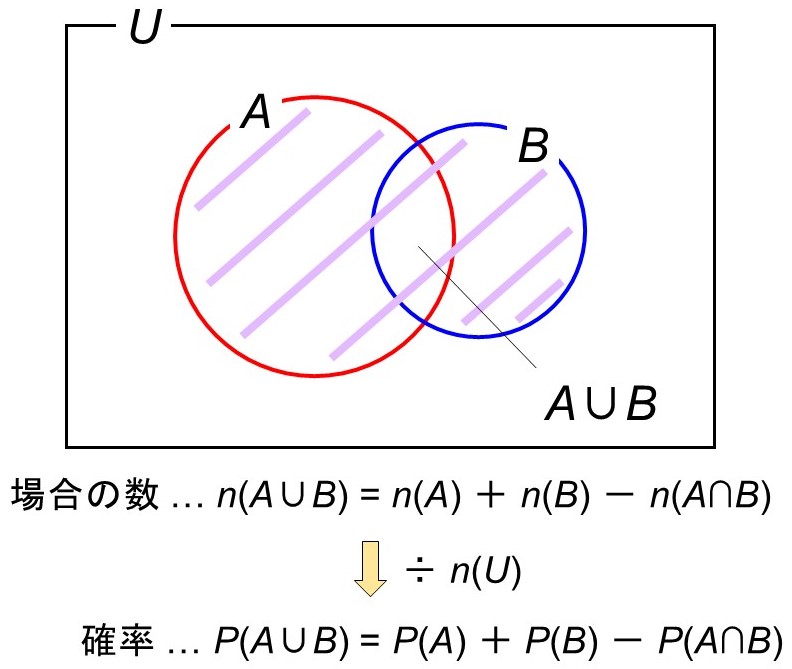
ある試行$\mathrm{T}$(試行は英語でTrialといいます)において、起こりうる事象に$A$、$B$があるとします。全事象を$U$とすると、前回学んだように、$A$が起こる確率$P(A)$、$B$が起こる確率$P(B)$、$A$と$B$が同時に起こる確率$P(A \cap B)$は次のように表すことができます。
$\begin{align}
&P(A) = \dfrac{n(A)}{n(U)}, \hspace{2pt} P(B)=\dfrac{n(B)}{n(U)}, \\[1.5ex]
&P(A \cap B)=\dfrac{n(A \cap B)}{n(U)}
\end{align}$
ここで、$A$または$B$が起こるという事象$A \cup B$について考えてみます。このように、和集合にあたる事象は和事象(わじしょう)と呼ばれます。
まず、確率$P(A \cup B)$は次のように表せます。
$P(A \cup B) = \dfrac{n(A \cup B)}{n(U)}$
一方、和集合の考え方を使うと、場合の数$n(A \cup B)$は次のように計算できます。
$n(A \cup B) = n(A)+n(B)-n(A \cap B)$
よって、$P(A \cup B)$は次のように変形することができます。
$\begin{align}
P(A \cup B) & = \dfrac{n(A \cup B)}{n(U)} \\[1.5ex]
& = \dfrac{n(A)+n(B)-n(A \cap B)}{n(U)} \\[1.5ex]
& = \dfrac{n(A)}{n(U)}+\dfrac{n(B)}{n(U)}-\dfrac{n(A \cap B)}{n(U)} \\[1.5ex]
& = P(A)+P(B)-P(A \cap B)
\end{align}$
つまり、場合の数と同じように確率も足し算・引き算を行うことができます。「同じ試行においては確率の分母($n(U)$)が変わらない」からですね。
ちなみに、確率のまま計算するメリットは2つあります。
- 各事象の確率だけ用意すればよいので、場合の数は各事象についてのみ数えればよい
- 複雑な事象の確率も簡単に計算できる
次の例を通して、これらの利点を理解していきましょう。
ここに9枚のカードがあり、それぞれには1~9の数字が書かれている。ここからランダムに1枚ずつ計3枚を取り出し、取り出した順に百の位、十の位、一の位とすることで3桁の数を作りたい。
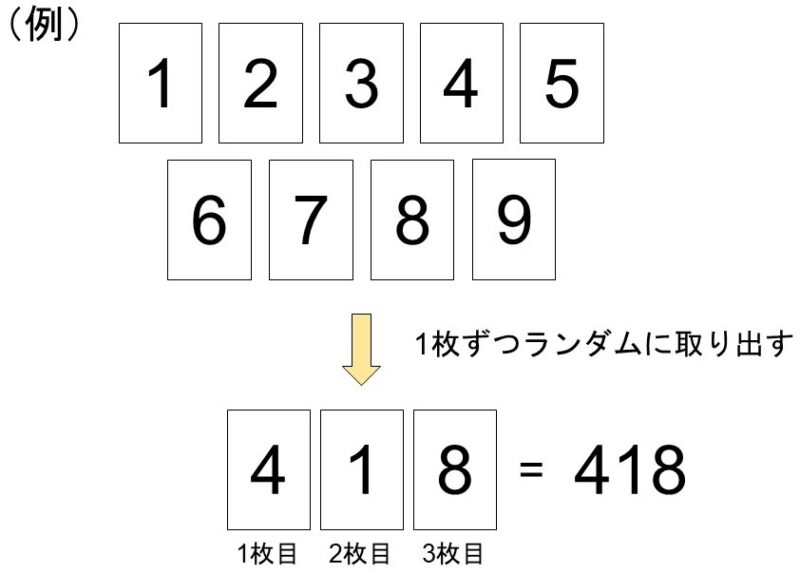
この時、次の確率はいくらになるか?
(1) 百の位が偶数または十の位が奇数である確率
(2) 一の位が2または4となる確率
(3) 各位のいずれかに7が使われる確率
(1) 百の位が偶数または十の位が偶数である確率
百の位が偶数となる事象を$A$、十の位が奇数となる事象を$B$とすると、求める確率$P(A \cup B)$は次のように表せます。
$P(A \cup B) = P(A)+P(B)-P(A \cap B)$
- $P(A)$
全事象を$U$とすると、$n(U)$、すなわち3桁の数の作り方は9個のものから順番に3個取り出して並べる順列とみなせるので、次のように計算できます(順列については21Fで解説しています)。
$n(U) = {}_9 \mathrm{P}_3 = 9 \times 8 \times 7$
百の位が偶数となる時、百の位は2, 4, 6, 8のカードの4通りであり、十の位と一の位は残りの8枚のカードから順番に選べばよいので、
$n(A) = 4 \times 8 \times 7$
よって、百の位が偶数となる確率$P(A)$は
$P(A) = \dfrac{n(A)}{n(U)}=\dfrac{4 \times 8 \times 7}{9 \times 8 \times 7} = \dfrac{4}{9}$
- $P(B)$
十の位が奇数となる時、十の位は1, 3, 5, 7, 9のカードの5通りであり、百の位と一の位は残り8枚のカードから順番に選べばよいので、
$n(B) = 5 \times 8 \times 7$
よって、十の位が奇数となる確率$P(B)$は
$P(B) = \dfrac{n(B)}{n(U)}=\dfrac{5 \times 8 \times 7}{9 \times 8 \times 7} = \dfrac{5}{9}$
- $P(A \cap B)$
百の位が偶数、十の位が奇数となる時、百の位は2, 4, 6, 8のカードの4通り、十の位は1, 3, 5, 7, 9のカードの5通り、一の位は残りの7枚のカードから選べばよいので、
$n(A \cap B) = 4 \times 5 \times 7$
よって、百の位が偶数かつ十の位が奇数となる確率$P(A \cap B)$は
$P(A \cap B) = \dfrac{n(A \cap B)}{n(U)} = \dfrac{4 \times 5 \times 7}{9 \times 8 \times 7} = \dfrac{5}{18}$
以上より、求める確率$P(A \cup B)$は
$\begin{align}
P(A \cup B) & = P(A)+P(B)-P(A \cap B) \\[1.5ex]
& = \dfrac{4}{9}+\dfrac{5}{9}-\dfrac{5}{18} \\[1.5ex]
& = \dfrac{13}{18}
\end{align}$
となります。
これまでは、場合の数$n(A \cup B)$を求めてから分数にして約分していたので、計算自体が大変でした。しかしこのように、各事象の確率を求めてから目的の確率を計算すると、比較的楽に計算ができます。
(2) 一の位が2または4となる確率
一の位が2となる事象を$C$、一の位が4となる事象を$D$とすると、求める確率$P(C \cup D)$は次のように表せます。
$P(C \cup D) = P(C)+P(D)-P(C \cap D)$
- $P(C)$
一の位が2となる場合、百の位と十の位は2のカードを除いた8枚のカードから選べばよいので、
$n(C) = 1 \times 8 \times 7$
よって、一の位が2となる確率$P(C)$は
$P(C) = \dfrac{1 \times 8 \times 7}{9 \times 8 \times 7} = \dfrac{1}{9}$
- $P(D)$
一の位が4となる確率$P(D)$については、$P(C)$と同じように考えることができるので、
$P(D) = \dfrac{1}{9}$
- $P(C \cap D)$
一の位が2かつ4となる事象$C \cap D$は起こりません($n(C \cap D)=0$)から、
$P(C \cap D) = 0$
以上より、求める確率$P(C \cup D)$は
$\begin{align}
P(C \cup D) & = P(C)+P(D) \\[1.5ex]
& = \dfrac{1}{9}+\dfrac{1}{9} \\[1.5ex]
& = \dfrac{2}{9}
\end{align}$
となります。今回の状況をベン図にすると次のようになりますね。
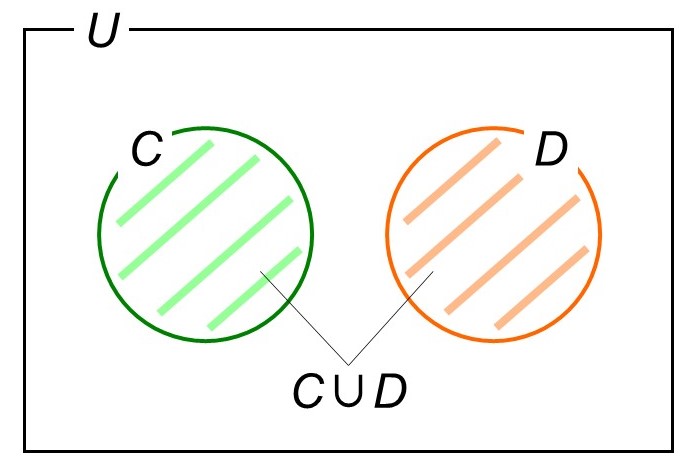
このように事象C、Dが同時に起こらない時、「CとDは排反(はいはん)である」といいます。事象が排反であれば、その和事象が起こる確率は各事象が起こる確率の足し算だけで求まります。
(3) 各位のいずれかに7が使われる確率
各位のいずれかに7が使われるという事象を$E$とします。確率$P(E)$を求める方法としては、次の2つが考えられます。
[1] 各位で場合分け(排反を使う)
実はこの問題、先ほど学んだ「排反」を使うことで計算できます。
百の位が7となる事象を$E_1$とします。この場合、十の位、一の位は残り8枚のカードから選べばよいので、場合の数は
$n(E_1) = 1 \times 8 \times 7$
よって、確率$P(E_1)$は
$P(E_1) = \dfrac{n(E_1)}{n(U)} = \dfrac{1 \times 8 \times 7}{9 \times 8 \times 7} = \dfrac{1}{9}$
十の位が7となる事象を$E_2$、一の位が7となる事象を$E_3$とすると、やはり$E_1$と同じように考えることができるので、これらの事象についても確率は同じです。
$P(E_2) = P(E_3) = \dfrac{1}{9}$
ところで、$E_1$、$E_2$、$E_3$は排反(同時に起こらない)ですから、求める確率$P(E)$は
$\begin{align}
P(E) & = P(E_1)+P(E_2)+P(E_3) \\[1.5ex]
& = \dfrac{1}{9}+\dfrac{1}{9}+\dfrac{1}{9} \\[1.5ex]
& = \dfrac{3}{9} = \dfrac{1}{3}
\end{align}$
となります。
[2] 余事象$E^c$に着目
反対に、どの位でも7が使われない事象$E^c$に注目してみましょう。このように、補集合にあたる事象は余事象(よじしょう)と呼ばれます。
すると、やはり場合の数の時と同じく、全事象が起こる確率$P(U)=1$から余事象が起こる確率$P(E^c)$を差し引くことで、$P(E)$を求めることができます。
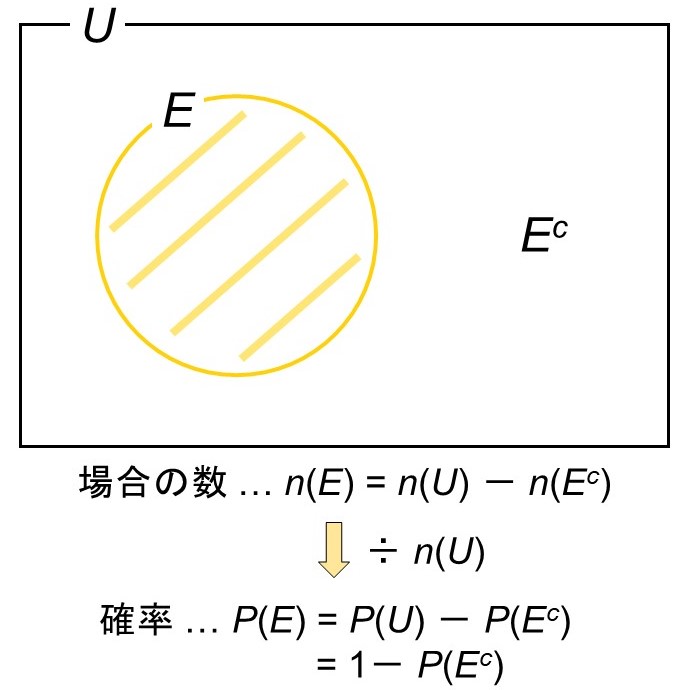
どの位でも7が使われない場合、残り8枚のカードを使って3桁の数を作ります。すなわち、8個のものから3個を選んで並べる順列を考えればよいので、場合の数$n(E^c)$は
$n(E^c) = {}_8 \mathrm{P}_3 = 8 \times 7 \times 6$
よって、確率$P(E^c)$は
$P(E^c) = \dfrac{n(E^c)}{n(U)} = \dfrac{8 \times 7 \times 6}{9 \times 8 \times 7} = \dfrac{2}{3}$
これより、求める確率$P(E)$は
$\begin{align}
P(E) & = 1-P(E^c) \\[1.5ex]
& = 1-\dfrac{2}{3} \\[1.5ex]
& = \dfrac{1}{3}
\end{align}$
となります。このように、余事象に着目すると、引き算を使って簡単に確率を求めることもできます。
確率の掛け算 ― 独立
次に、確率の掛け算ができる場面について学んでいきます。
2つの試行$\mathrm{T}_1$(全事象$U_1$)と$\mathrm{T}_2$(全事象$U_2$)はお互いの結果に影響をあたえないとします。この時、「$\mathrm{T}_1$と$\mathrm{T}_2$は独立(どくりつ)である」といいます。例えば、コイントスを2回行う場合、1回目と2回目の試行は独立です。
また、試行$\mathrm{T}_1$で起こりうる事象として$A$が、試行$\mathrm{T}_2$で起こりうる事象として$B$があるとすると、確率$P(A)$と$P(B)$は次のように表せます。
$P(A) = \dfrac{n(A)}{n(U_1)}, \hspace{2pt} P(B) = \dfrac{n(B)}{n(U_2)}$
ここで、$\mathrm{T}_1$と$\mathrm{T}_2$を行った時に$A$かつ$B$が起こるという事象$A \cap B$について考えてみます。このように、共通部分にあたる事象は積事象(せきじしょう)と呼ばれます。
$\mathrm{T}_1$と$\mathrm{T}_2$の両方について考えた場合、全事象における場合の数は$n(U_1) \times n(U_2)$、$A$かつ$B$が起こる場合の数は$n(A) \times n(B)$ですから、確率$P(A \cap B)$は次のように表せます。
$\begin{align}
P(A \cap B) & = \dfrac{n(A) \times n(B)}{n(U_1) \times n(U_2)} \\[1.5ex]
& = \dfrac{n(A)}{n(U_1)} \times \dfrac{n(B)}{n(U_2)} \\[1.5ex]
& = P(A) \times P(B)
\end{align}$
すなわち$A$かつ$B$が起こる確率は、$A$が起こる確率$P(A)$と$B$が起こる確率$P(B)$の掛け算として表せます。
このように、独立な試行によって積事象が起こる確率は、各試行での確率の掛け算で計算できます。
わかりやすい例で考えてみましょう。
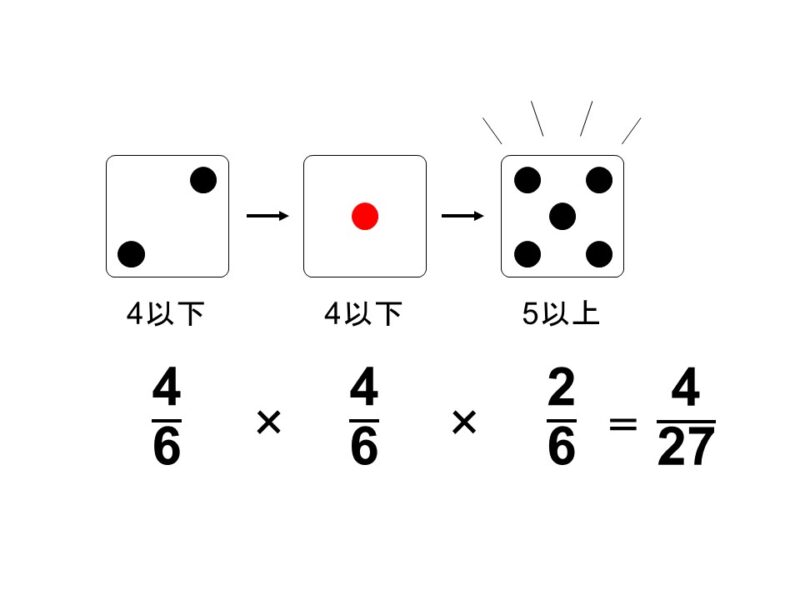
サイコロが1個あり、これを5以上の目が出るまで振り続けるとする。
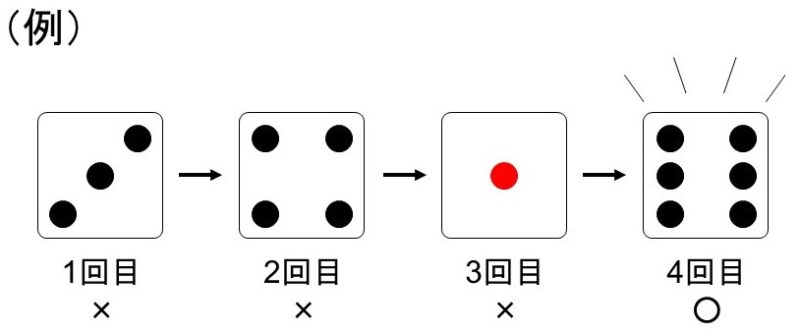
この時、3回目でサイコロを振り終える確率はいくらか?
まず「サイコロを振る」という試行ですが、前後の結果に影響することはないので、独立です。
3回目でサイコロを振り終えるということは、1回目と2回目は4以下の目(1, 2, 3, 4)が出て、3回目で初めて5以上の目(5, 6)が出ることになります。
4以下の目が出る確率は
$\dfrac{4}{6} = \dfrac{2}{3}$
5以上の目が出る確率は
$\dfrac{2}{6} = \dfrac{1}{3}$
なので、求める確率は
$\dfrac{2}{3} \times \dfrac{2}{3} \times \dfrac{1}{3} = \dfrac{4}{27}$
と計算できます。こちらについても、直接場合の数を求めてから分数にして約分するという手順ではない分、楽に計算ができます。
確率の割り算 ― 条件付き確率
最後は、確率の割り算についてです。こちらは例を通して説明したいと思います。
AさんはBさんにとあるゲームをもちかけた。5つのコップのうち2つに玉を入れてシャッフルし、どのコップに玉が入っているかを互いに当てるというゲームである。
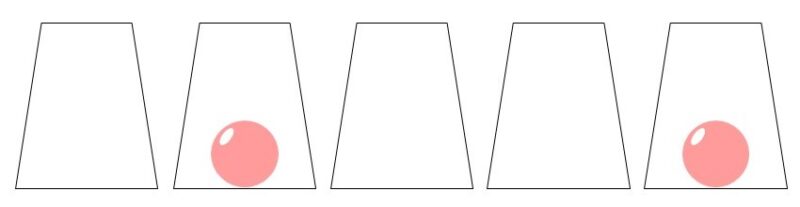
この時、次の確率はいくらか?
(1) Aさんは空のコップを選び、Bさんは玉の入ったコップを選ぶ確率
(2) Aさんが空のコップを引いたとわかっている状態で、Bさんが玉の入ったコップを選ぶ確率
あらかじめ、全事象$U$における場合の数$n(U)$を求めておきましょう。
Aさん → Bさんの順にコップを選んだとすると、Aさんのコップの選び方は5通り、Bさんのコップの選び方は4通りなので、
$n(U)=5 \times 4 = 20$
となります。
(1) Aさんは空のコップを選び、Bさんは玉の入ったコップを選ぶ確率
「Aさんが空のコップを選ぶ」という事象を$A_\text{×}$、「Bさんが玉の入ったコップを選ぶ」という事象を$B_\text{○}$とします。
今回の事象$A_\text{×} \cap B_\text{○}$において、Aさんのコップの選ぶ方は3通り、Bさんのコップの選び方は2通りなので、場合の数は
$n(A_\text{×} \cap B_\text{○}) = 3 \times 2 = 6$
よって、求める確率は
$P(A_\text{×} \cap B_\text{○}) = \dfrac{n(A_\text{×} \cap B_\text{○})}{n(U)} = \dfrac{6}{20} = \dfrac{3}{10}$
となります。ここまでは今まで通りですね。
(2) Aさんが空のコップを選んだとわかっている状態で、Bさんが玉の入ったコップを選ぶ確率
「Aさんが空のコップを選んだ」という情報が最初からある場合、確率はどう考えればよいのでしょうか?この場合、確率の分母となる全事象の数が変わります。
すなわち、Aさんが空のコップを選ぶ場合($A_\text{×}$)の下で起こりうる事象だけを考えればよいので、全事象における場合の数は$n(A_\text{×})$とすることができます。
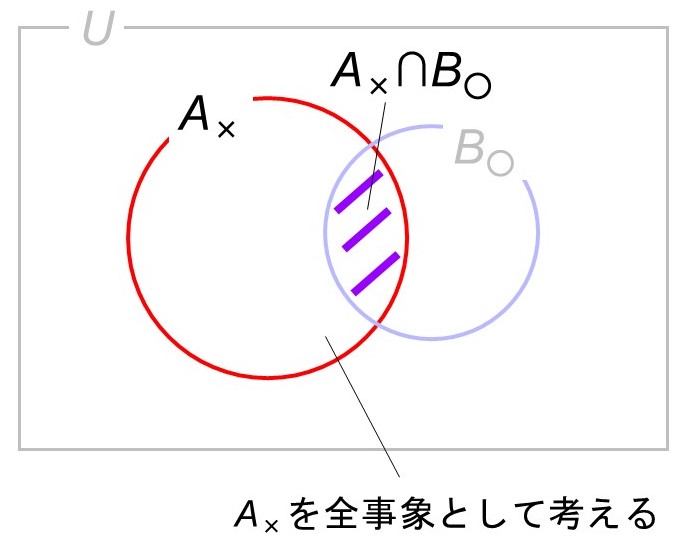
Aさんが空のコップを選ぶ場合、Aさんのコップの選び方は3通り(空のコップ)、Bさんはコップの選び方は4通り(残りのコップ)ですから、
$n(A_\text{×}) = 3 \times 4 = 12$
よって、今回の確率は次のように計算できます。
$\dfrac{n(A_\text{×} \cap B_\text{○})}{n(A_\text{×})} = \dfrac{6}{12} = \dfrac{1}{2}$
このように、起こりうる事象についてわかっている情報がある場合の確率を条件付き確率といい、
$P_{A_\text{×}}(B_\text{○})$
のように表します。条件付き確率を考える時は、その情報に基づいて全事象における場合の数を変える必要があります。
ところで、今求めた確率の式は次のようになっていました。
$P_{A_\text{×}}(B_\text{○}) = \dfrac{n(A_\text{×} \cap B_\text{○})}{n(A_\text{×})}$
この右辺の分母・分子を全事象における場合の数$n(U)$で割るとどうなるでしょうか?すると、場合の数で表していた分母・分子は確率を使っても表せることがわかります。
$\begin{align}
P_{A_\text{×}}(B_\text{○}) & = \dfrac{n(A_\text{×} \cap B_\text{○})}{n(A_\text{×})} \\[1.5ex]
& = \dfrac{\dfrac{n(A_\text{×} \cap B_\text{○})}{n(U)}}{\dfrac{n(A_\text{×})}{n(U)}} \\[1.5ex]
& = \dfrac{P(A_\text{×} \cap B_\text{○})}{P(A_\text{×})}
\end{align}$
このように、条件付き確率は確率の割り算としても計算することができます。
まとめ
今回は確率の四則演算とその意味について学びました。内容が盛りだくさんでしたので、簡単にまとめておきます。
- 集合(ベン図)を基にした場合の数の足し算・引き算は、確率でも同じようにできる
$P(A \cup B) = P(A)+P(B)-P(A \cap B)$
(排反なら$P(A \cup B) = P(A)+P(B)$)
$P(A)=1-P(A^c)$(余事象に着目)
- 2つの試行がお互いの結果に影響をあたえない時、それらは独立であるといい、積事象(それぞれの試行で同時に起こる事象)の確率を掛け算で求めることができる
$P(A \cap B) = P(A)P(B)$
- ある条件や情報があたえられた上での確率を条件付き確率といい、確率の割り算として求めることができる
$P_A(B) = \dfrac{n(A \cap B)}{n(A)} = \dfrac{P(A \cap B)}{P(A)}$
これらを理解して使いこなせるようになると、確率の計算がより簡単に行えるようになります。必要に応じてどんどん活用していきましょう。
今回はここまでです。お疲れさまでした!