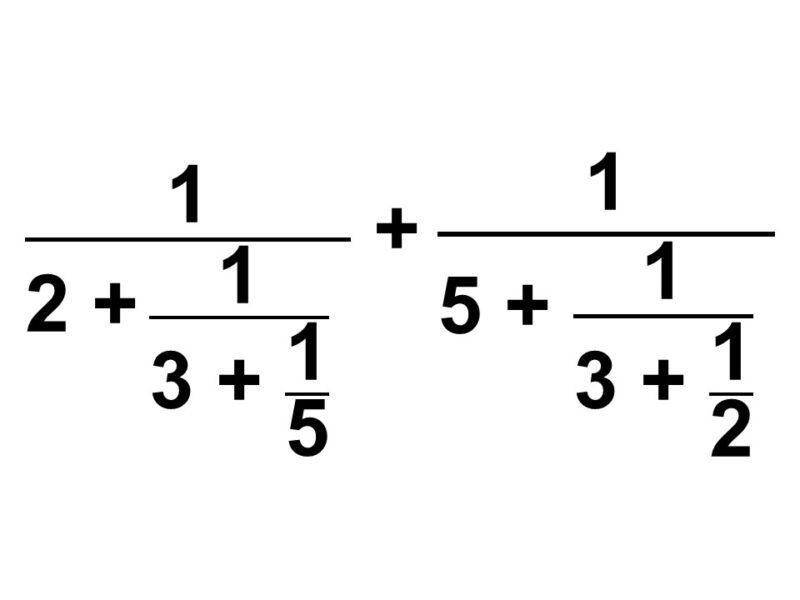今回の問題はこちらです。(※15Fまでの内容を理解していることが前提です!)
次の式を計算してください。
$\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{5}}}+\dfrac{1}{5+\dfrac{1}{3+\dfrac{1}{2}}}$
分数が入れ子になっていて見た目がすごいですね…このような分数は連分数(れんぶんすう)と呼ばれます。さて、どう計算したらよいでしょうか?
基本に立ち返って考えよう
見たことがないものが出てきた時は基本に戻って考えましょう。分数に対してできることは「分母と分子に同じ数を掛けても割ってもよい」でした(13Fを参照してください)。これを使って分数を整理していきます。
第1項(+でつながっているそれぞれの数を項といいます)から整理しましょう。この時、入れ子の内側に着目します。
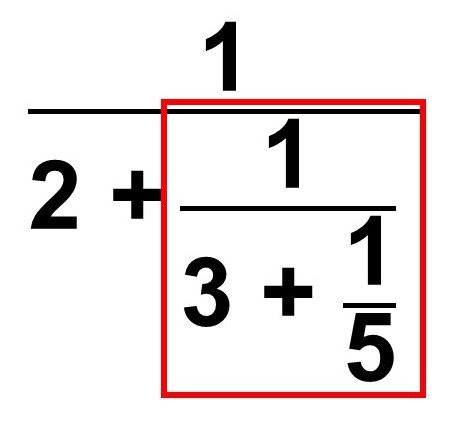
この分数の分母・分子に対して、その中にある分数($\frac{1}{5}$)の分母である5を掛けてみます。すると、
$\begin{align}
\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{5}}} & = \dfrac{1}{2+\dfrac{1 \times 5}{(3+\dfrac{1}{5}) \times 5}} \\[1.5ex]
& = \dfrac{1}{2+\dfrac{5}{3 \times 5+\dfrac{1}{5} \times 5}} \\[1.5ex]
& = \dfrac{1}{2+\dfrac{5}{15+1}} \\[1.5ex]
& = \dfrac{1}{2+\dfrac{5}{16}} \\[1.5ex]
\end{align}$
となります(1段目から2段目の変形では分配法則を使っています)。少しすっきりしましたね。
続いては、分数全体に着目します。

分母・分子に対し、その内側にある分数($\frac{5}{16}$)の分母である16を掛けてみます。すると、
$\begin{align}
\dfrac{1}{2+\dfrac{5}{16}} & = \dfrac{1 \times 16}{(2+\dfrac{5}{16}) \times 16} \\[1.5ex]
& = \dfrac{16}{2 \times 16+\dfrac{5}{16} \times 16} \\[1.5ex]
& = \dfrac{16}{32+5} \\[1.5ex]
& = \dfrac{16}{37}
\end{align}$
となり、単純な分数にできました。
このように、連分数は「内側にある分数の分母を全体の分母・分子に掛ける」ことで簡単にすることができます。
15Fでは、割り算を掛け算に直す時に分母・分子に分母の逆数を掛ける操作を行っていますが、今回の考え方はこれに少し似ていますね。合わせて確認してみてください。
同じようにして、第2項も整理してみましょう。
$\begin{align}
\dfrac{1}{5+\dfrac{1}{3+\dfrac{1}{2}}} & = \dfrac{1}{5+\dfrac{1 \times 2}{(3+\dfrac{1}{2}) \times 2}} \\[1.5ex]
& = \dfrac{1}{5+\dfrac{2}{6+1}} \\[1.5ex]
& = \dfrac{1}{5+\dfrac{2}{7}} \\[1.5ex]
& = \dfrac{1 \times 7}{(5+\dfrac{2}{7}) \times 7} \\[1.5ex]
& = \dfrac{7}{35+2} \\[1.5ex]
& = \dfrac{7}{37}
\end{align}$
以上から、
$\begin{align}
& \hspace{13pt} \dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{5}}}+\dfrac{1}{5+\dfrac{1}{3+\dfrac{1}{2}}} \\[1.5ex]
& = \dfrac{16}{37}+\dfrac{7}{37} \\[1.5ex]
& = \dfrac{16+7}{37} \\[1.5ex]
& = \dfrac{23}{37}
\end{align}$
となります。
連分数で無理数を表す
別の機会に詳しくお話ししますが、実は数の世界には普通の分数では表せない数があります。
このような数は無理数(むりすう)と呼ばれ、例えば$\sqrt{2}$(読み方は「ルート2」、2回かけると2になる数)という無理数は通常の分数で表すことはできません。
しかし、連分数を使うと$\sqrt{2}$は次のように表すことができます。
$\sqrt{2} = 1+\dfrac{1}{2+\dfrac{1}{2+\dfrac{1}{\text{…}}}}$
…の部分には同じ形が続いていきます。このように連分数は、数の表し方にさらなる可能性を与えてくれる方法となっています。