こんにちは、まてがめです。
内心・傍心に続き、前回は三角形と円を結びつける図形の性質「外心・垂心」について学びました。
今回も「円の内側」に注目していきます。第2部にあたる今回は円周角の定理について学びます。
円周角の定理は有名な定理の1つですが、とりわけ使い勝手がよく、例えば接弦定理や方べきの定理といった円における重要な定理も、この定理を使うと簡単に示すことができます。
円周角の定理そのものを証明するのは少し手間(ただし難しくはない)ですが、平面図形を理解していく上でとても便利な道具なので、なぜ成り立つのかも含め、この階でバッチリ身につけちゃいましょう!
円周角の定理
弧・弦・中心角
内容に入る前に、あらかじめ理解が必要な用語があるので、先にそちらを確認しておきましょう。
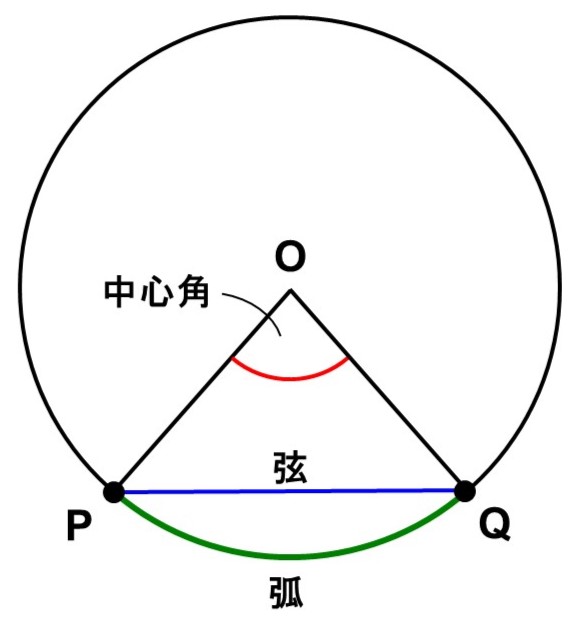
円$\mathrm{O}$の周上に2点$\mathrm{P}$, $\mathrm{Q}$をとります。この時、$\mathrm{PQ}$がなす円周の一部を弧(こ)といい、$\stackrel{\huge \frown}{\mathrm{PQ}}$と表します。一方、$\mathrm{P}$, $\mathrm{Q}$を直接結んでできる線分$\mathrm{PQ}$を弦(げん)といいます。
また、$\mathrm{O}$, $\mathrm{P}$, $\mathrm{Q}$によってできる図形は、その形から扇形(おうぎがた)と呼ばれ、$\angle \mathrm{POQ}$を$\stackrel{\huge \frown}{\mathrm{PQ}}$に対する中心角(ちゅうしんかく)といいます(練習問題T9でも解説しています)。
円周角の定理とは?
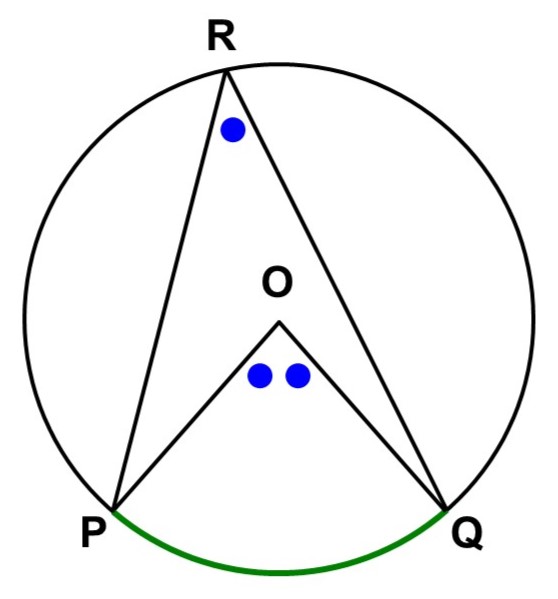
ここで、$\stackrel{\huge \frown}{\mathrm{PQ}}$を除く円周上に点$\mathrm{R}$があるとします。この時、$\angle \mathrm{PRQ}$を$\stackrel{\huge \frown}{\mathrm{PQ}}$に対する円周角(えんしゅうかく)といいます。
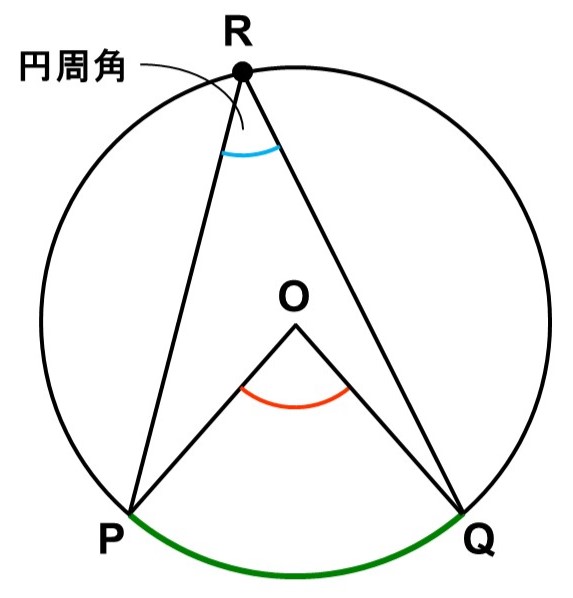
そして、この円周角$\angle \mathrm{PRQ}$は必ず中心角$\angle \mathrm{POQ}$の半分になります。これが円周角の定理と呼ばれるものです。
$\mathrm{PRQ} = \dfrac{\angle \mathrm{POQ}}{2}$
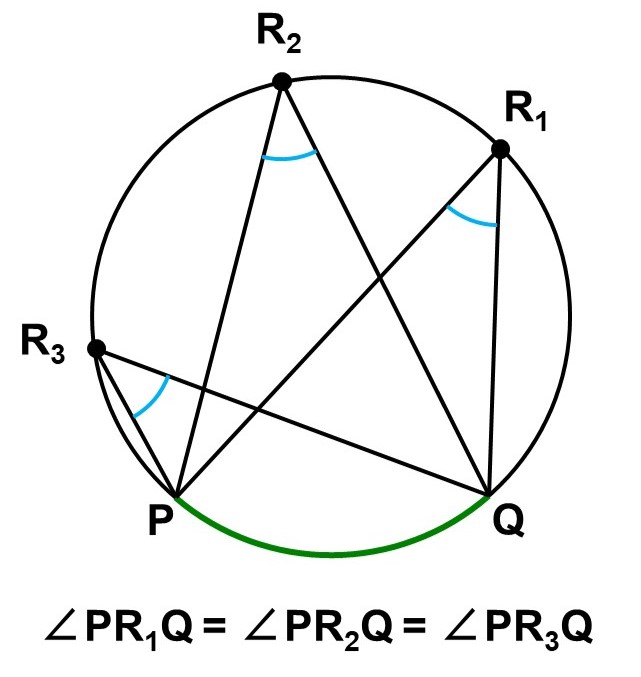
この定理で重要なのは、$\mathrm{R}$の位置については「$\stackrel{\huge \frown}{\mathrm{PQ}}$を除く円周上」としか言っていないことです。
つまり、これさえ満たしていれば円周角は必ず同じ大きさ($中心角の半分)になるということです。この性質も円周角の定理と呼ばれています。
二等辺三角形を使うと円周角の定理を証明できる
では、この不思議な定理を証明してみましょう。使うのは基本的に二等辺三角形だけですが、「中心角(円周角)の大きさ」と「円周角の頂点の位置」に注目して、ていねいに場合分けを行う必要があります[1], [2]。
(命題)
円$\mathrm{O}$の周上に2点$\mathrm{P}$, $\mathrm{Q}$をとり、$\stackrel{\huge \frown}{\mathrm{PQ}}$を除く任意の円周上に点$\mathrm{R}$をとる。この時、次が成り立つ。
$\angle \mathrm{PRQ} = \dfrac{\angle \mathrm{POQ}}{2}$
(証明)
中心角$\angle \mathrm{POQ}$の大きさにもとづいて、次のように場合分けして考える。
(1) $0^{\circ} < \angle \mathrm{POQ} < 180^{\circ}$の時
この時、$\mathrm{R}$の位置によって、さらに次の3通りが考えられる。
(1-a) 直線$\mathrm{OR}$上に$\mathrm{P}$または$\mathrm{Q}$が存在する時
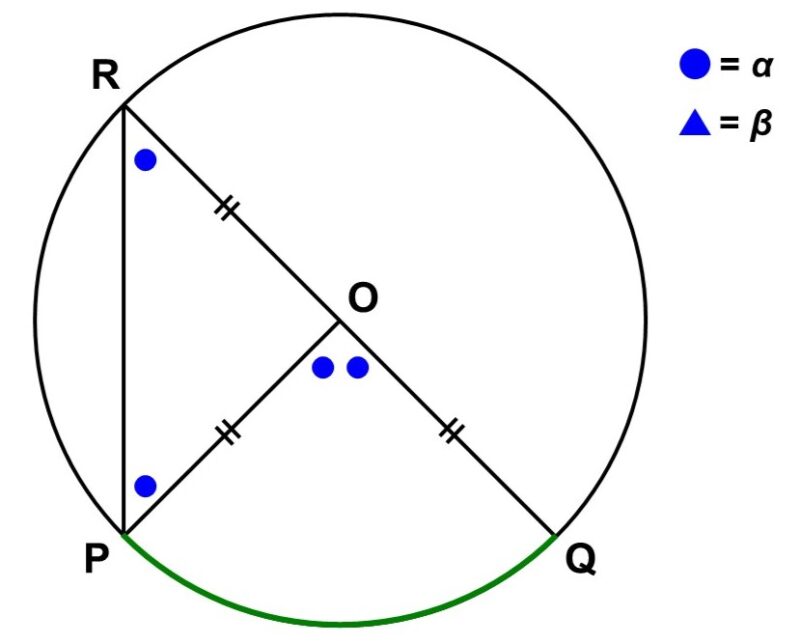
例えば直線$\mathrm{OR}$上に$\mathrm{Q}$が存在する場合、$\angle \mathrm{PRQ} = \alpha$とすると、円の定義から、$\triangle \mathrm{ORP}$は$\mathrm{OR} = \mathrm{OP}$の二等辺三角形なので、
$\angle \mathrm{ORP} = \angle \mathrm{OPR} = \alpha$
中心角$\angle \mathrm{POQ}$は、ちょうど$\triangle \mathrm{ORP}$の外角でもあり、
$\begin{align}
\angle \mathrm{POQ} &= \angle \mathrm{ORP}+\angle \mathrm{OPR} \\[1.5ex]
&= 2 \times \alpha
\end{align}$
つまり、円周角$\angle \mathrm{PRQ}(\angle \mathrm{ORP})$は中心角$\angle \mathrm{POQ}$の半分である。
(1-b) 直線$\mathrm{OR}$と$\stackrel{\huge \frown}{\mathrm{PQ}}$が、$\mathrm{P}$, $\mathrm{Q}$と異なる点$\mathrm{S}$で交わる時
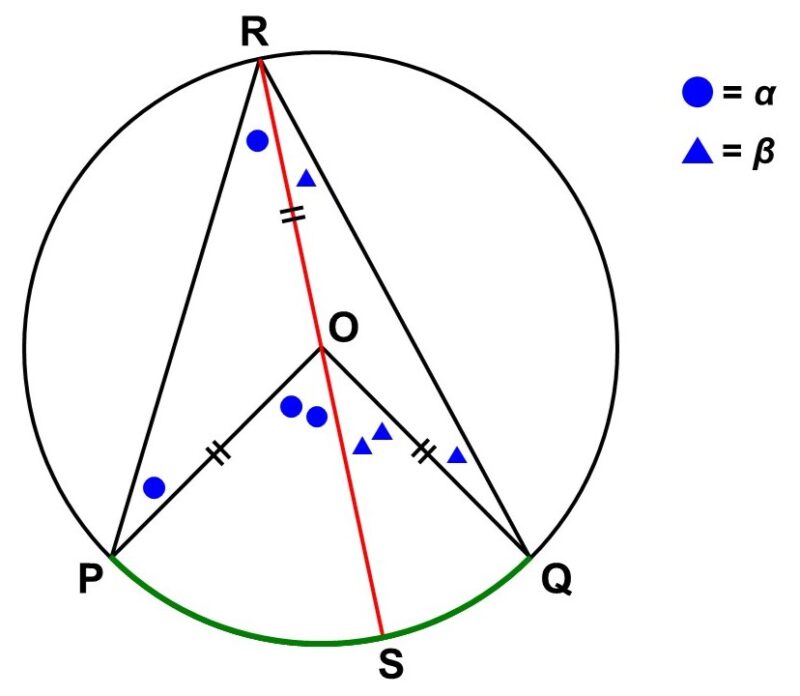
$\triangle \mathrm{ORP}$, $\triangle \mathrm{ORQ}$は二等辺三角形なので、
$\angle \mathrm{ORP} = \angle \mathrm{OPR} = \alpha$
$\angle \mathrm{ORQ} = \angle \mathrm{OQR} = \beta$
と表せる。ここで各三角形の外角に注目すると、
$\begin{align}
\angle \mathrm{POS} &= \angle \mathrm{ORP}+\angle \mathrm{OPR} \\[1.5ex]
&= 2 \alpha
\end{align}$
(以降×の記号は省略)
$\begin{align}
\angle \mathrm{QOS} &= \angle \mathrm{ORQ}+\angle \mathrm{OQR} \\[1.5ex]
&= 2 \beta
\end{align}$
よって、円周角$\angle \mathrm{PQR}$と中心角$\angle \mathrm{POR}$はそれぞれ次のように表せる。
$\begin{align}
\angle \mathrm{PRQ} &= \angle \mathrm{ORP}+\angle \mathrm{ORQ} \\[1.5ex]
&= \alpha+\beta
\end{align}$
$\begin{align}
\angle \mathrm{POQ} &= \angle \mathrm{POS}+\angle \mathrm{QOS} \\[1.5ex]
&= 2 \alpha+2 \beta \\[1.5ex]
&= 2(\alpha+\beta)
\end{align}$
つまり、円周角$\angle \mathrm{PQR}$は中心角$\angle \mathrm{POQ}$の半分である。
(1-c) 直線$\mathrm{OR}$が$\stackrel{\huge \frown}{\mathrm{PQ}}$と交わらない時
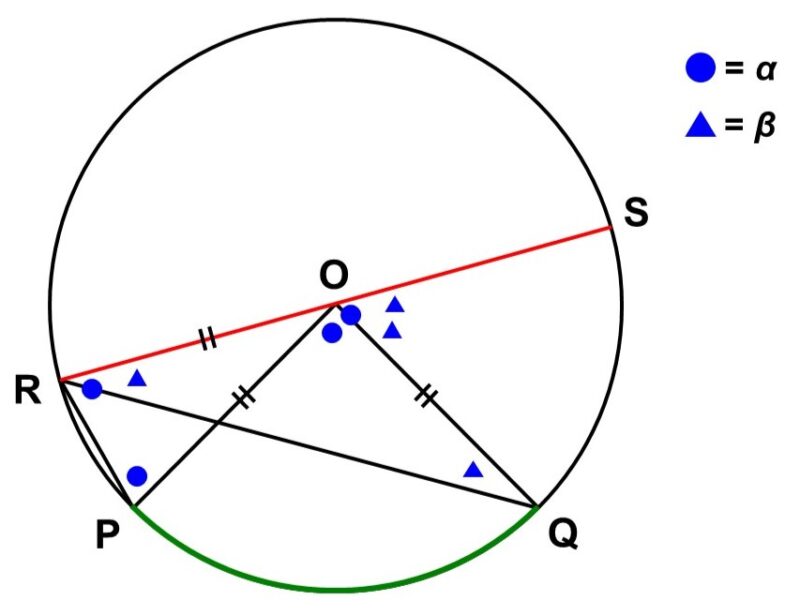
直線$\mathrm{OR}$と円$\mathrm{O}$の交点を$\mathrm{S}$とする。
$\triangle \mathrm{ORP}$, $\triangle \mathrm{ORQ}$は二等辺三角形なので、
$\angle \mathrm{ORP} = \angle \mathrm{OPR} = \alpha$
$\angle \mathrm{ORQ} = \angle \mathrm{OQR} = \beta$
と表せる。ここで各三角形の外角に注目すると、
$\begin{align}
\angle \mathrm{POS} &= \angle \mathrm{ORP}+\angle \mathrm{OPR} \\[1.5ex]
&= 2 \alpha
\end{align}$
$\begin{align}
\angle \mathrm{QOS} &= \angle \mathrm{ORQ}+\angle \mathrm{OQR} \\[1.5ex]
&= 2 \beta
\end{align}$
よって、円周角$\angle \mathrm{PQR}$と中心角$\angle \mathrm{POR}$はそれぞれ次のように表せる。
$\begin{align}
\angle \mathrm{PRQ} &= \angle \mathrm{ORP}-\angle \mathrm{ORQ} \\[1.5ex]
&= \alpha-\beta
\end{align}$
$\begin{align}
\angle \mathrm{POQ} &= \angle \mathrm{POS}-\angle \mathrm{QOS} \\[1.5ex]
&= 2 \alpha-2 \beta \\[1.5ex]
&= 2(\alpha-\beta)
\end{align}$
つまり、円周角$\angle \mathrm{PQR}$は中心角$\angle \mathrm{POQ}$の半分である。
よって(1-a), (1-b), (1-c)から、(1)の場合において命題は真である。
(2) $\angle \mathrm{POQ} = 180^{\circ}$の時
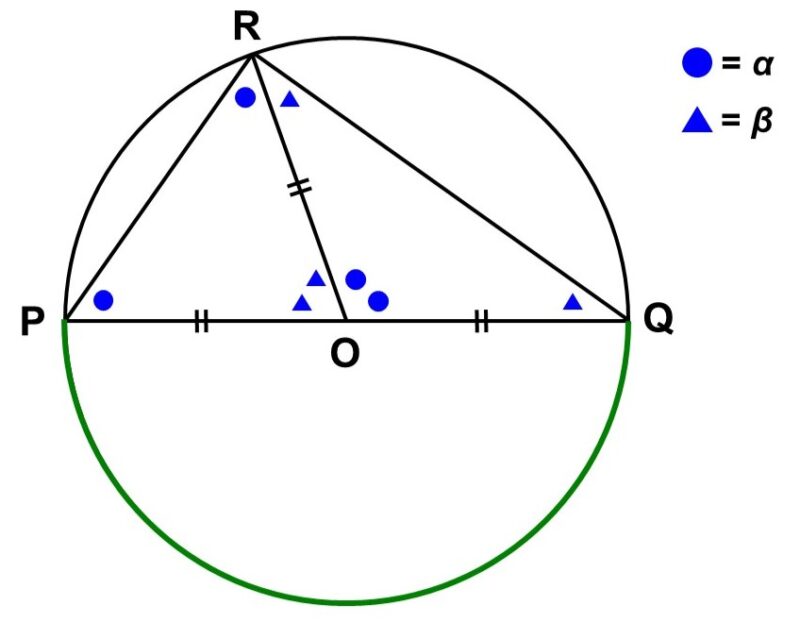
$\triangle \mathrm{ORP}$, $\triangle \mathrm{ORQ}$は二等辺三角形なので、
$\angle \mathrm{ORP} = \angle \mathrm{OPR} = \alpha$
$\angle \mathrm{ORQ} = \angle \mathrm{OQR} = \beta$
と表せる。ここで各三角形の外角に注目すると、
$\begin{align}
\angle \mathrm{QOR} &= \angle \mathrm{ORP}+\angle \mathrm{OPR} \\[1.5ex]
&= 2 \alpha
\end{align}$
$\begin{align}
\angle \mathrm{POR} &= \angle \mathrm{ORQ}+\angle \mathrm{OQR} \\[1.5ex]
&= 2 \beta
\end{align}$
よって、円周角$\angle \mathrm{PQR}$と中心角$\angle \mathrm{POR}$はそれぞれ次のように表せる。
$\begin{align}
\angle \mathrm{PRQ} &= \angle \mathrm{ORP}+\angle \mathrm{ORQ} \\[1.5ex]
&= \alpha+\beta
\end{align}$
$\begin{align}
\angle \mathrm{POQ} &= \angle \mathrm{QOR}+\angle \mathrm{POR} \\[1.5ex]
&= 2 \alpha+2 \beta \\[1.5ex]
&= 2(\alpha+\beta) \\[1.5ex]
\end{align}$
つまり、円周角$\angle \mathrm{PQR}$は中心角$\angle \mathrm{POQ}$の半分であり、この場合において命題は真である。
(3) $180^{\circ} < \angle \mathrm{POQ} < 360^{\circ}$の時
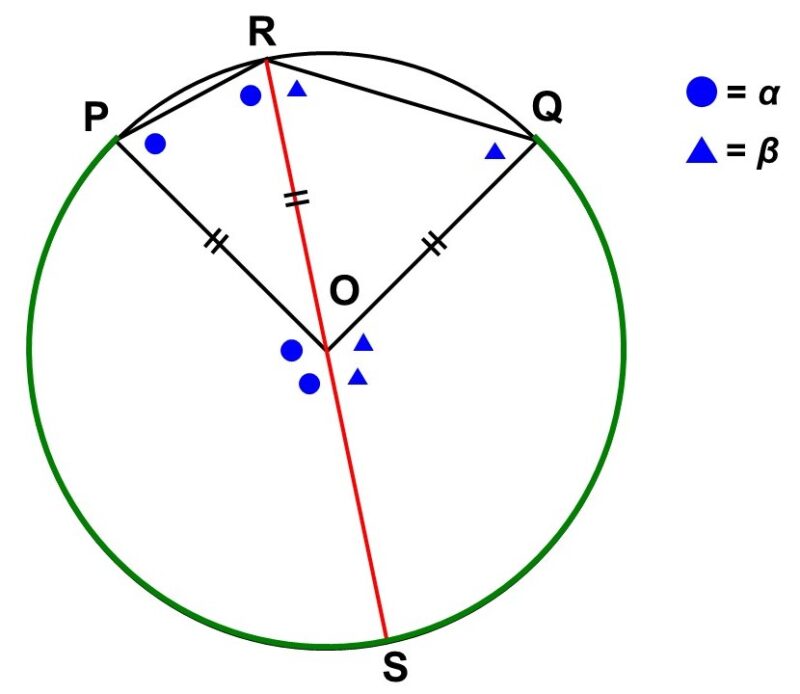
直線$\mathrm{OR}$と円$\mathrm{O}$の交点を$\mathrm{S}$とする。
$\triangle \mathrm{ORP}$, $\triangle \mathrm{ORQ}$は二等辺三角形なので、
$\angle \mathrm{ORP} = \angle \mathrm{OPR} = \alpha$
$\angle \mathrm{ORQ} = \angle \mathrm{OQR} = \beta$
と表せる。ここで各三角形の外角に注目すると、
$\begin{align}
\angle \mathrm{POS} &= \angle \mathrm{ORP}+\angle \mathrm{OPR} \\[1.5ex]
&= 2 \alpha
\end{align}$
$\begin{align}
\angle \mathrm{QOS} &= \angle \mathrm{ORQ}+\angle \mathrm{OQR} \\[1.5ex]
&= 2 \beta
\end{align}$
よって、円周角$\angle \mathrm{PQR}$と中心角$\angle \mathrm{POR}$はそれぞれ次のように表せる。
$\begin{align}
\angle \mathrm{PRQ} &= \angle \mathrm{ORP}+\angle \mathrm{ORQ} \\[1.5ex]
&= \alpha+\beta
\end{align}$
$\begin{align}
\angle \mathrm{POQ} &= \angle \mathrm{POS}+\angle \mathrm{QOS} \\[1.5ex]
&= 2 \alpha+2 \beta \\[1.5ex]
&= 2(\alpha+\beta)
\end{align}$
つまり、円周角$\angle \mathrm{PQR}$は中心角$\angle \mathrm{POQ}$の半分であり、この場合において命題は真である。
以上(1), (2), (3)より、命題は真であることが示せた。
(証明終)
円周角の定理は「中心角の半分になる」、「頂点をどこにとっても角度が変わらない」という2つからなりますが、エッセンスは「元になっている弧の長さによってのみ角度が決まる」ということです。
例えば、円$\mathrm{O}$において、$\stackrel{\huge \frown}{\mathrm{AB}}$からなる円周角$\angle \mathrm{APB}$と$\stackrel{\huge \frown}{\mathrm{CD}}$からなる円周角$\angle \mathrm{CQD}$があり、$\stackrel{\huge \frown}{\mathrm{AB}} = \stackrel{\huge \frown}{\mathrm{CD}}$が成り立っているとします。
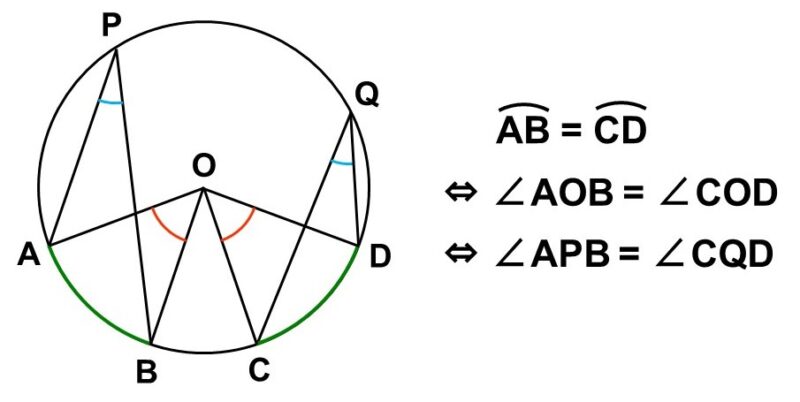
この時、弧の長さはそのまま中心角の大きさに対応するので、中心角においても$\angle \mathrm{AOB} = \angle \mathrm{COD}$が成り立ちます。
そして、円周角は必ず中心角の半分になるので、結局$\angle \mathrm{APB} = \angle \mathrm{CQD}$も成り立つわけです。
これは逆に考えることもでき、
円周角が等しい → 対応する中心角が等しい → 対応する弧の長さが等しい
という関係でもあります。
この1対1対応の考え方は重要なので、よく覚えておきましょう。
接弦定理
接弦定理とは?
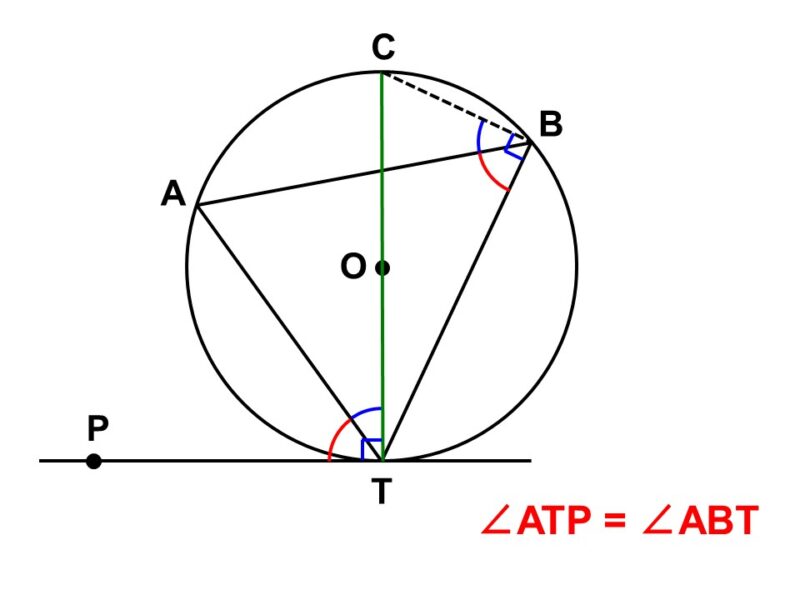
円における重要な定理の1つに接弦定理(せつげんていり)と呼ばれる定理があります[3], [4]。その名の通り、接線と弦に関する定理です(接線については35Fで解説しています)。
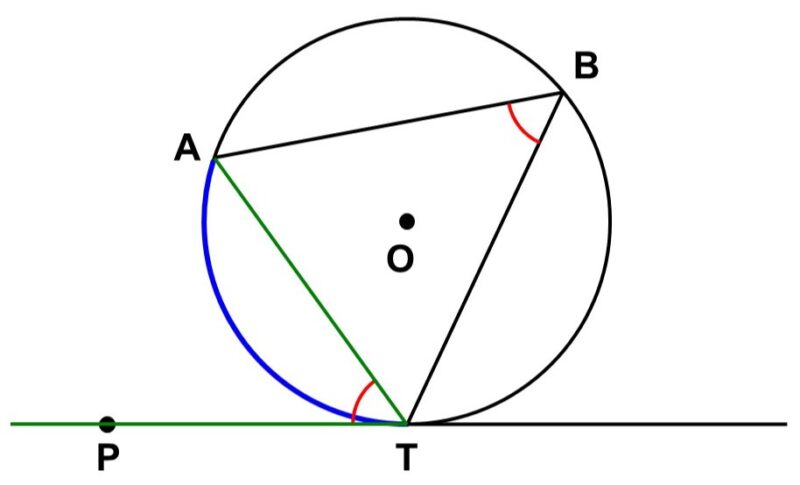
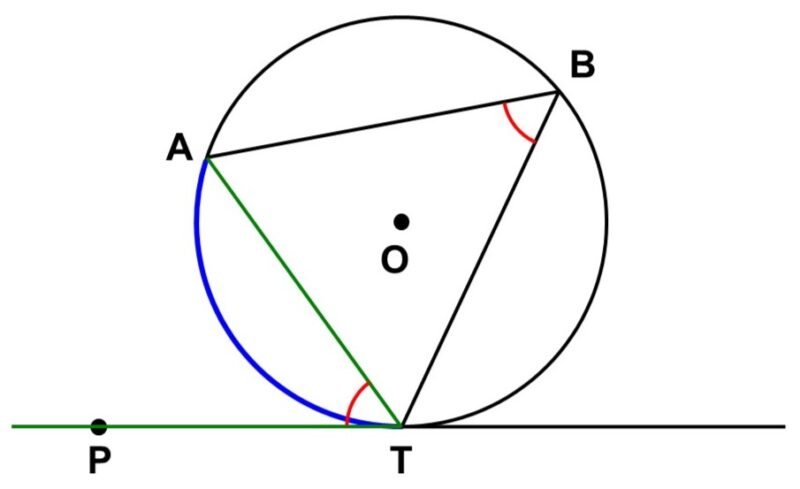
図のように、円$\mathrm{O}$に対して、$\mathrm{T}$を接点とする接線$\mathrm{PT}$と$\mathrm{T}$を端点とする弦$\mathrm{AT}$があるとします。
この時、接線$\mathrm{PT}$と弦$\mathrm{AT}$がなす$\angle \mathrm{ATP}$は、$\angle \mathrm{ATP}$の内側にある$\stackrel{\huge \frown}{\mathrm{AT}}$に対する円周角$\angle \mathrm{ABT}$に等しくなります。
$\angle \mathrm{ABT} = \angle \mathrm{ATP}$
この定理も一見すると不思議に思えますね。接弦定理は、例えば次のような場面で活躍します。
(例)
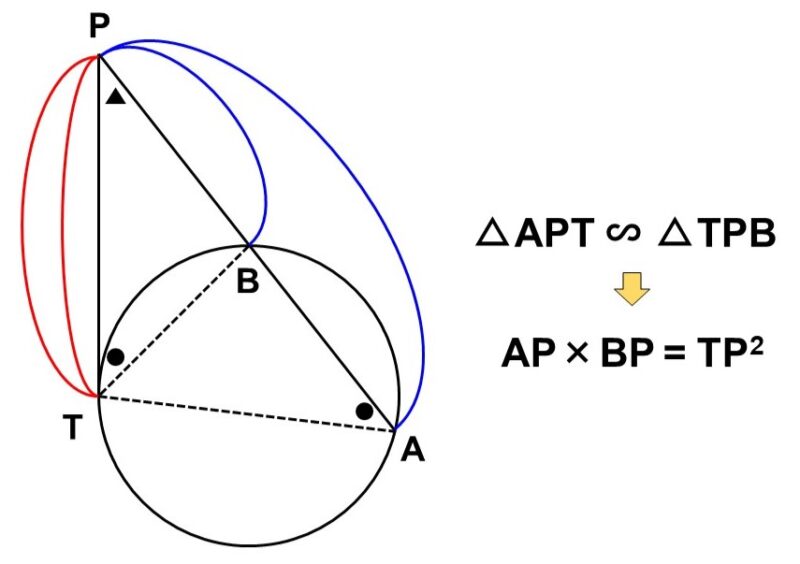
円$\mathrm{O}$において、直線$\mathrm{AB}$と接線$\mathrm{PT}$が点$\mathrm{P}$で交わっている。$\mathrm{AB} = 3$, $\mathrm{BP} = 1$の時、$\mathrm{PT}$の長さを求めてみよう。
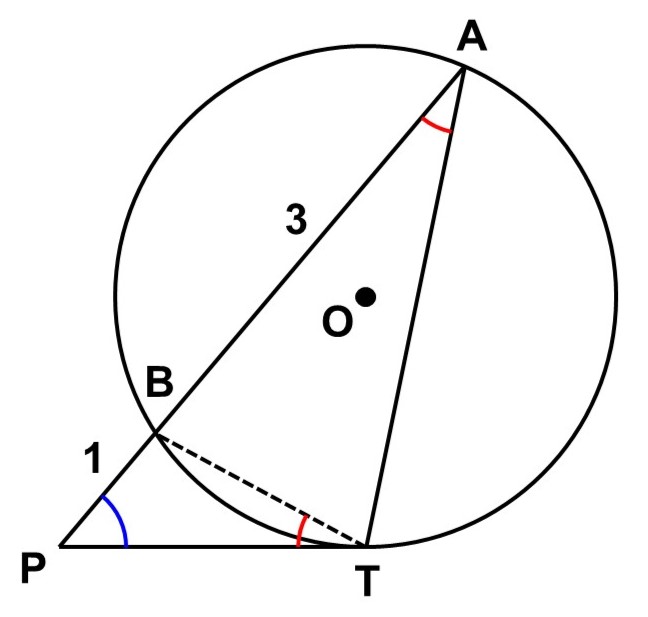
$\triangle \mathrm{TPB}$と$\triangle \mathrm{APT}$について、次のことが言える。
- $\angle \mathrm{TPB} = \angle \mathrm{APT}$ <1>
- 接線$\mathrm{PT}$と弦$\mathrm{BT}$について、接弦定理より、
$\angle \mathrm{BTP} = \angle \mathrm{TAP}$ <2>
<1>, <2>より、$\triangle \mathrm{TPB}$と$\triangle \mathrm{APT}$は2つの角がそれぞれ等しいので、相似である。
よって、対応する辺の比率が等しく、
$\dfrac{\mathrm{TP}}{\mathrm{AP}} = \dfrac{\mathrm{PB}}{\mathrm{PT}}$
両辺に$\mathrm{AP}$, $\mathrm{PT}$を掛けると、
$\begin{align}
&\hspace{27pt} \dfrac{\mathrm{TP}}{\cancel{\mathrm{AP}}} \times \cancel{\mathrm{AP}} \times \mathrm{PT} = \dfrac{\mathrm{PB}}{\cancel{\mathrm{PT}}} \times \mathrm{AP} \times \cancel{\mathrm{PT}} \\[1.5ex]
&\iff \mathrm{PT}^2 = \mathrm{PB} \times \mathrm{PA} <3>
\end{align}$
$\mathrm{PB} = 1$, $\mathrm{PA} = 1+3 = 4$なので、式<3>は
$\begin{align}
&\hspace{27pt} \mathrm{PT}^2 = 1 \times 4 = 4 (= 2^2) \\[1.5ex]
&\iff \mathrm{PT} = 2
\end{align}$
円周角の定理から接弦定理が導ける
この定理、実は先ほど紹介した円周角の定理を使うと、次のように証明ができます[3]。
(命題)
円$\mathrm{O}$に対して、$\mathrm{T}$を接点とする接線$\mathrm{PT}$と$\mathrm{T}$を端点とする弦$\mathrm{AT}$があるとする。
この時、接線$\mathrm{PT}$と弦$\mathrm{AT}$がなす角$\angle \mathrm{ATP}$は、$\angle \mathrm{ATP}$の内側にある$\stackrel{\huge \frown}{\mathrm{AT}}$に対する円周角$\angle \mathrm{ABT}$に等しくなる。
$\angle \mathrm{ATP} = \angle \mathrm{ABT}$
(証明)
(1) $\angle \mathrm{ATP}$が直角の時
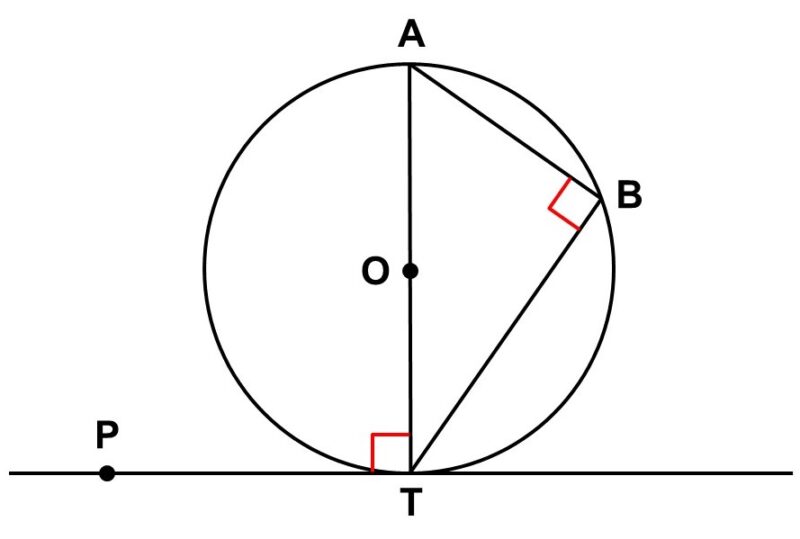
$\mathrm{PT}$は接線なので、$\mathrm{PT} \perp \mathrm{OT}$が成り立っている。つまり$\angle \mathrm{ATP} = 90^{\circ}$の時、$\mathrm{TA}$は中心$\mathrm{O}$を通る直径に相当している。
よって、$\stackrel{\huge \frown}{\mathrm{TA}}$について円周角の定理より、
$\begin{align}
\angle \mathrm{ABT} &= \dfrac{\angle \mathrm{TOA}}{2} \\[1.5ex]
&= \dfrac{180^{\circ}}{2} = 90^{\circ}
\end{align}$
ゆえに、$\angle \mathrm{ATP} = \angle \mathrm{ABT} (= 90^{\circ})$である。
(2) $\angle \mathrm{ATP}$が鋭角の時
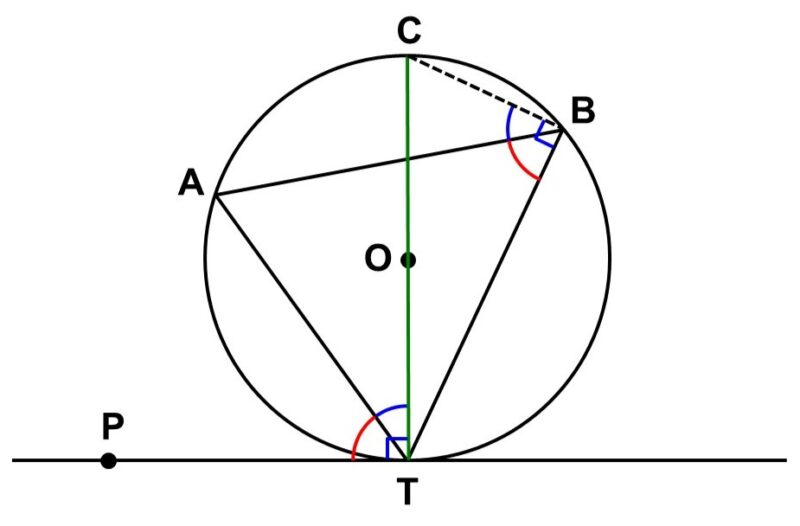
中心$\mathrm{O}$を通る直線$\mathrm{TC}$を引く。
$\mathrm{PT}$は接線なので、
$\angle \mathrm{CTP} = 90^{\circ}$
$\stackrel{\huge \frown}{\mathrm{TC}}$について円周角の定理より、
$\begin{align}
\angle \mathrm{TBC} &= \dfrac{\angle \mathrm{TOC}}{2} \\[1.5ex]
&= \dfrac{180^{\circ}}{2} = 90^{\circ}
\end{align}$
よって、
$\angle \mathrm{CTP} = \angle \mathrm{TBC} = 90^{\circ}$ <1>
また、$\stackrel{\huge \frown}{\mathrm{AC}}$について円周角の定理より、
$\angle \mathrm{CTA} = \angle \mathrm{ABC}$ <2>
<1>, <2>より、
$\begin{align}
\angle \mathrm{ATP} &= \angle \mathrm{CTP}-\angle \mathrm{CTA} \\[1.5ex]
&= \angle \mathrm{TBC}-\angle \mathrm{ABC} \\[1.5ex]
&= \angle \mathrm{ABT}
\end{align}$
(3) $\angle \mathrm{ATP}$が鈍角の時
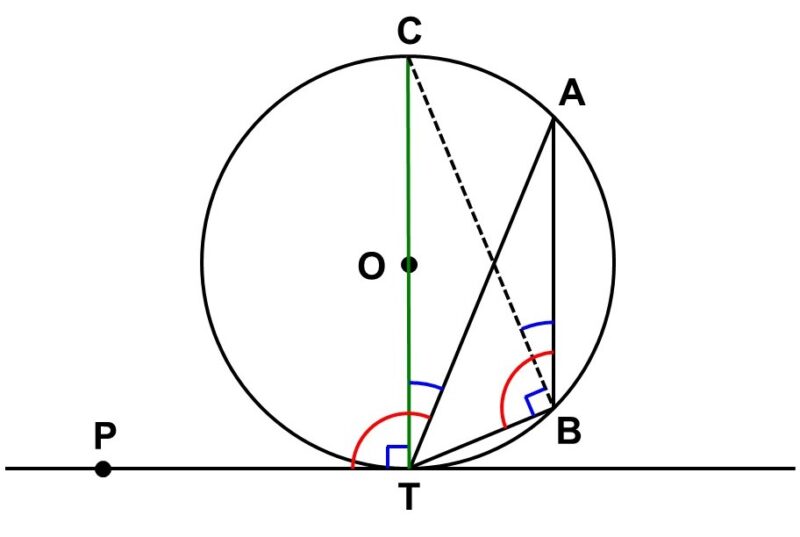
中心$\mathrm{O}$を通る直線$\mathrm{TC}$を引く。
(2)の場合と同じように考えると、
$\angle \mathrm{CTP} = \angle \mathrm{TBC} = 90^{\circ}$ <3>
$\angle \mathrm{CTA} = \angle \mathrm{ABC}$ <4>
が成り立つ。よって<3>, <4>より、
$\begin{align}
\angle \mathrm{ATP} &= \angle \mathrm{CTP}+\angle \mathrm{CTA} \\[1.5ex]
&= \angle \mathrm{TBC}+\angle \mathrm{ABC} \\[1.5ex]
&= \angle \mathrm{ABT}
\end{align}$
以上(1), (2), (3)より、命題は真であることが示せた。
(証明終)
方べきの定理
円周角の定理が「相似」を保証してくれる
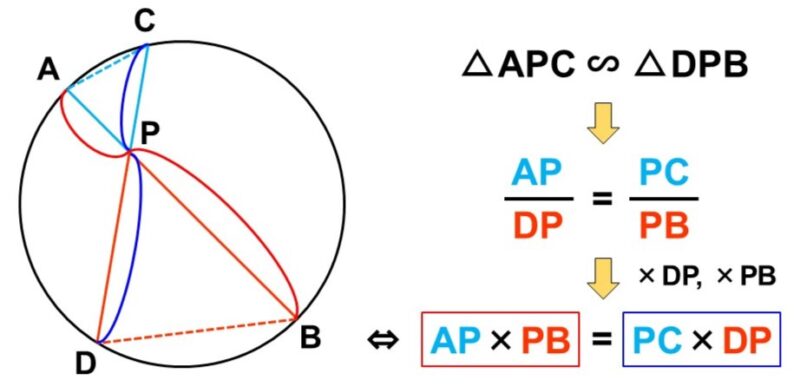
状況にもよりますが、円の内側にある三角形は「相似」になっていることがよくあります。
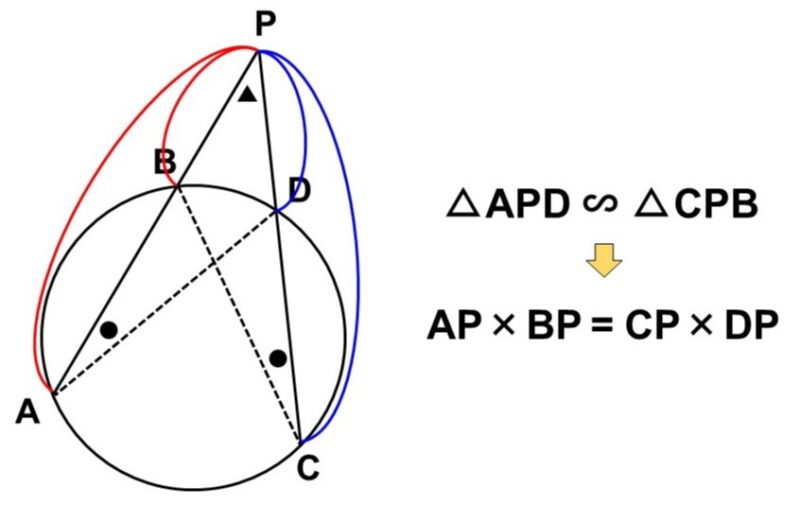
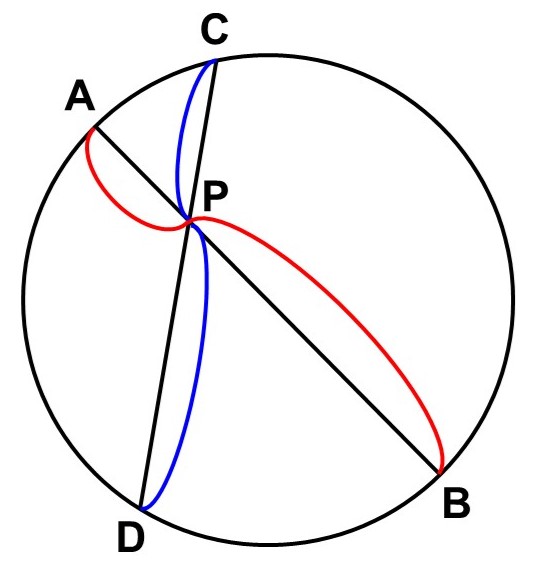
例えば、円上に4点$\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$, $\mathrm{D}$があり、直線$\mathrm{AB}$, $\mathrm{CD}$が円の内部の点$\mathrm{P}$で交わっているとします。
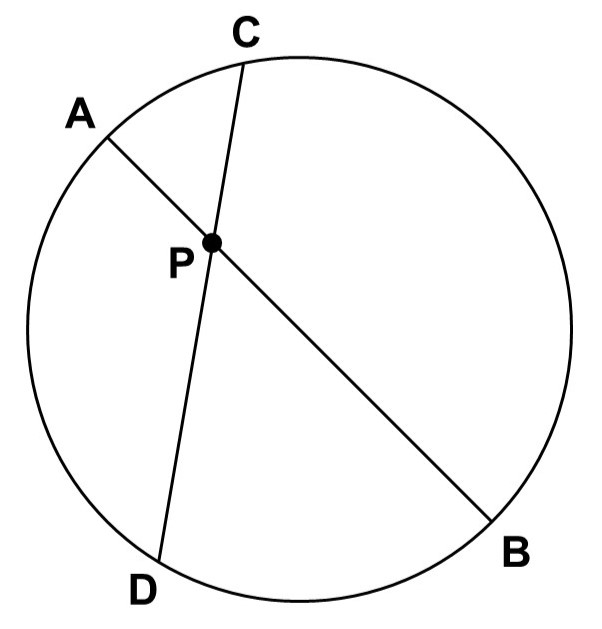
ここで、$\triangle \mathrm{APC}$, $\triangle \mathrm{DPB}$に注目すると、円周角の定理から
$\angle \mathrm{PCA} = \angle \mathrm{PBD}$
($\stackrel{\huge \frown}{\mathrm{AD}}$に対する円周角)
$\angle \mathrm{CAP} = \angle \mathrm{BDP}$
($\stackrel{\huge \frown}{\mathrm{BC}}$に対する円周角)
が成り立ちます。つまり、2つの角がそれぞれ等しいので、この2つの三角形は相似です。
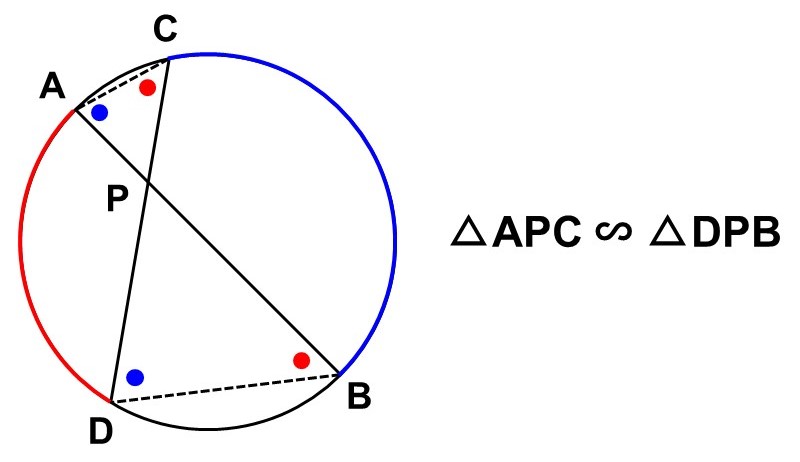
このように円の内部に三角形ができる場合、相似が成り立つことが多く、それは円周角の定理によって保証されます。
方べきの定理とは?
実はこの話を掘り下げていくと、方べきの定理と呼ばれる不思議な定理にたどり着きます。
先ほどの図において、$\triangle \mathrm{APC}$ ∽ $\triangle \mathrm{DPB}$が成り立つということは、対応する辺の比率は等しいので、
$\dfrac{\mathrm{AP}}{\mathrm{DP}} = \dfrac{\mathrm{PC}}{\mathrm{PB}}$
が成り立ちます。ここで分母を消して式を見やすくするため、両辺に$\mathrm{DP}$, $\mathrm{PB}$を掛けてみると、次のような不思議な関係式が出てきます。
$\begin{align}
&\hspace{30pt} \dfrac{\mathrm{AP}}{\mathrm{DP}} = \dfrac{\mathrm{PC}}{\mathrm{PB}} \\[1.5ex]
&\iff \dfrac{\mathrm{AP}}{\cancel{\mathrm{DP}}} \times \cancel{\mathrm{DP}} \times \mathrm{PB} = \dfrac{\mathrm{PC}}{\cancel{\mathrm{PB}}} \times \mathrm{DP} \times \cancel{\mathrm{PB}} \\[1.5ex]
&\iff \mathrm{AP} \times \mathrm{PB} = \mathrm{PC} \times \mathrm{DP}
\end{align}$
これが方べきの定理と呼ばれるもので、四角形の対角線のように掛け算を行っているのが特徴です。
円の内部で2本の線が交差しているような時には、常にこのシンプルな関係式を使うことができます。三角比とならんで、相似を使いやすくするためのツールとして覚えておくとよいでしょう。
(例)
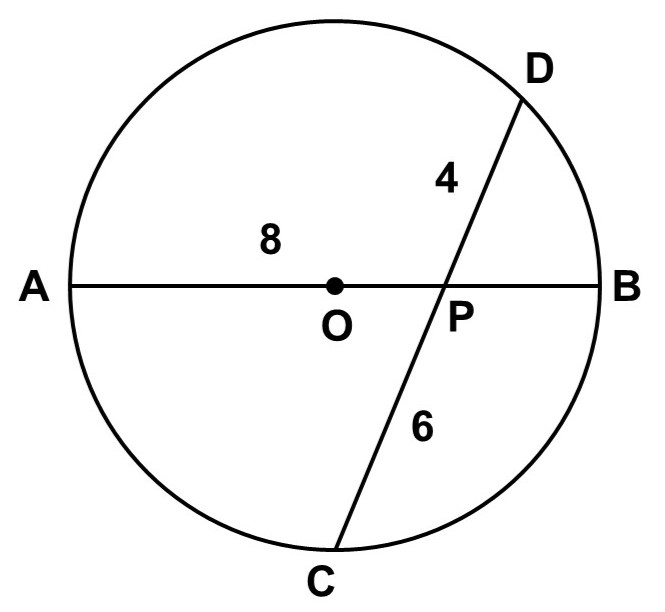
円$\mathrm{O}$の周上に点$\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$, $\mathrm{D}$があり、$\mathrm{AB}$, $\mathrm{CD}$は点$\mathrm{P}$で交わっている。また、線分$\mathrm{AB}$は円の中心$\mathrm{O}$を通る。
$\mathrm{AP} = 8$, $\mathrm{CP} = 6$, $\mathrm{DP} = 4$の時、円$\mathrm{O}$の直径を求めてみよう。
線分$\mathrm{AB}$, $\mathrm{CD}$と交点$\mathrm{P}$について、方べきの定理より、
$\begin{align}
&\hspace{27pt} \mathrm{AP} \times \mathrm{PB} = \mathrm{CP} \times \mathrm{PD} \\[1.5ex]
&\iff 8 \times \mathrm{PB} = 6 \times 4 \\[1.5ex]
&\iff \mathrm{PB} = 3
\end{align}$
よって、円$\mathrm{O}$の直径は
$\begin{align}
\mathrm{AB} &= \mathrm{AP}+\mathrm{PB} \\[1.5ex]
&= 8+3 = 11
\end{align}$
まとめ
今回は円周角の定理とそこから導かれる定理(接弦定理・方べきの定理)について学びました。定理の中身をもう一度確認しておきましょう。
- 円周角の定理:
円$\mathrm{O}$の周上に2点$\mathrm{P}$, $\mathrm{Q}$をとり、$\stackrel{\huge \frown}{\mathrm{PQ}}$を除く任意の円周上に点$\mathrm{R}$をとる。この時、次が成り立つ。
$\angle \mathrm{PRQ} = \dfrac{\angle \mathrm{POQ}}{2}$
- 接弦定理:
円$\mathrm{O}$に対して、$\mathrm{T}$を接点とする接線$\mathrm{PT}$と$\mathrm{T}$を端点とする弦$\mathrm{AT}$があるとする。この時、接線$\mathrm{PT}$と弦$\mathrm{AT}$がなす$\angle \mathrm{ATP}$は、$\angle \mathrm{ATP}$の内側にある$\stackrel{\huge \frown}{\mathrm{AT}}$に対する円周角$\angle \mathrm{ABT}$に等しくなる。
$\angle \mathrm{ATP} = \angle \mathrm{ABT}$
- 方べきの定理:
円$\mathrm{O}$の周上に4点$\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$, $\mathrm{D}$があり、直線$\mathrm{AB}$, $\mathrm{CD}$が円の内部$\mathrm{P}$で交わっているとする。この時、次が成り立つ。
$\mathrm{AP} \times \mathrm{PB} = \mathrm{CP} \times \mathrm{PD}$
円周角の定理は、円について考えるための基本ツールです。円に関する問題を解く中で、もし接弦定理や方べきの定理を忘れてしまったり、どこから取りかかればよいかわからなくなってしまった時は、まず円周角の定理を使えないか考えてみることをオススメします。
今回はここまでです。お疲れ様でした!
参考文献
[1] 東大の先生!文系の私に超わかりやすく数学を教えてください! (西成活裕 / かんき出版 2019)
[2] カジュアルな算数・数学の話 (鶴崎修功 / クラーケンラボ 2021)
[3] チャート式 基礎からの数学Ⅰ+A 新課程 (チャート研究所 / 数研出版 2022)
[4] 中学 自由自在 数学 (井上栄二(監修:秋山仁) / 受験研究社 2021)