T7　「三角比にかくされた関係、あなたは導けますか？」 ― 倍角の公式

こんにちは、まてがめです。

今回の問題は全部で4問あります（※32Fまでの内容を前提とします）。問題文が少し長いですが、ぜひ登場人物になったつもりで考えてみてください。

32Fで直角三角形から定義される三角比について学んだ千春（ちはる）さんは、三角比の持つ性質に興味をもった。

そこで千春さんはまず、三角比を扱いやすくするための工夫として、斜辺の長さが1、鋭角の1つが角度$\theta$の直角三角形$\mathrm{ABC}$から考えていくことにした。

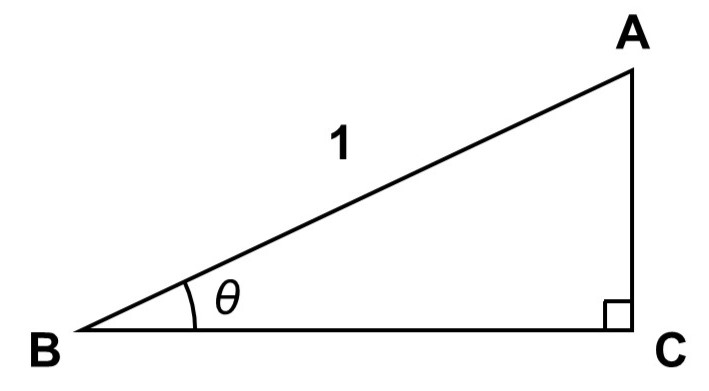
(1) 直角三角形$\mathrm{ABC}$について、辺$\mathrm{BC}$, $\mathrm{CA}$の長さを求めなさい。

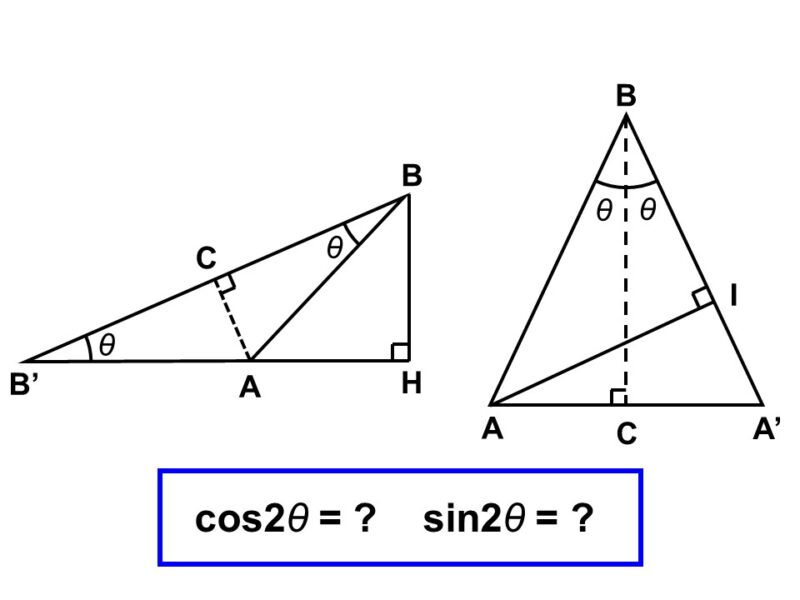
千春さんは、2つの直角三角形$\mathrm{ABC}$を辺$\mathrm{CA}$でつないで二等辺三角形$\mathrm{ABB’}$を作り、これを含む直角三角形$\mathrm{BB’H}$を考えることで、2倍角$2 \theta$（×の記号は省略）の三角比を表せることに気がついた。

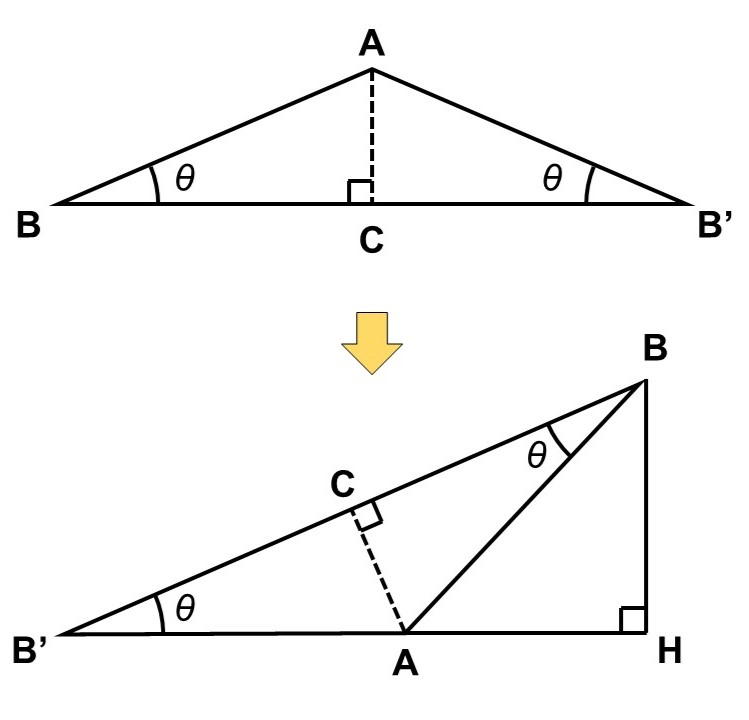
(2) 二等辺三角形$\mathrm{ABB’}$および直角三角形$\mathrm{BB’H}$を使って、$\cos 2 \theta$, $\sin 2 \theta$を求めなさい。

また千春さんは、2倍角の三角比を求める別の方法として、直角三角形$\mathrm{ABC}$を辺$\mathrm{BC}$でつないで二等辺三角形$\mathrm{BAA’}$を作り、頂点$\mathrm{A}$から辺$\mathrm{BA’}$に垂線$\mathrm{AI}$を下ろしてできる直角三角形$\mathrm{BAI}$を使えないかと考えた。

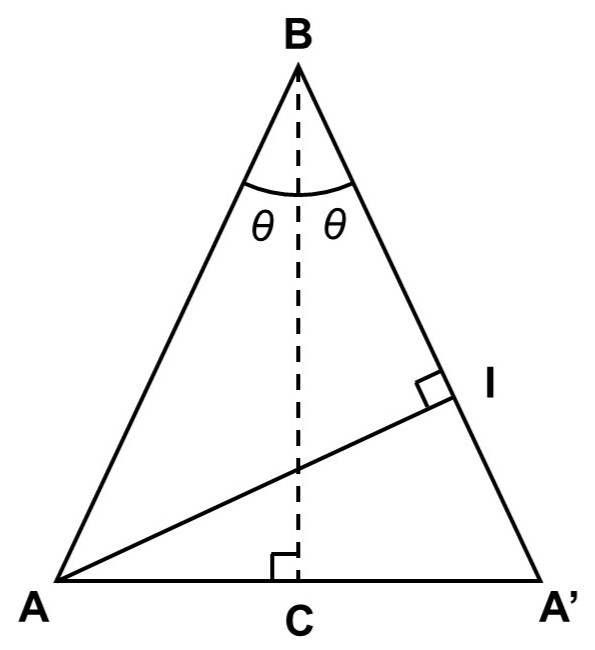
(3) 二等辺三角形$\mathrm{BAA’}$および直角三角形$\mathrm{BAI}$を使って、$\cos 2 \theta$, $\sin 2 \theta$を求めなさい。

(3)の結果は(2)の結果と少し異なっていたが、計算ミスはしていなかったので、千春さんは$\cos \theta$と$\sin \theta$のあいだに特別な関係があるのではないかと考えた。

そこで千春さんは、(2), (3)の結果を使い、$\cos \theta$と$\sin \theta$の関係式を求めてみることにした。

(4) (2), (3)の結果から、$\cos^2 \theta+\sin^2 \theta = 1$が成り立つことを示しなさい。

三角比には多くの有名公式がありますが、その1つに倍角の公式があります。この問題は、その公式を図形的に求めてみようというお話です。

(1) まずは三角比の復習から…

(1)は斜辺が1の直角三角形に対して、残りの辺の長さを求める問題です。

まずは復習ですが、三角比$\cos \theta$, $\sin \theta$は次のように定義されます。

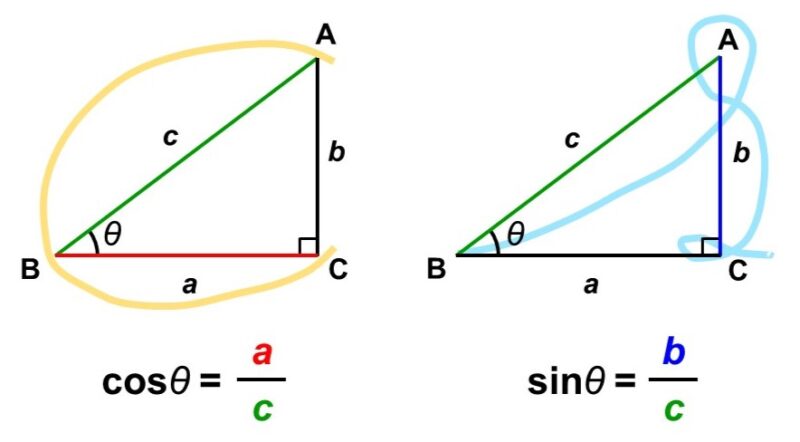
これは言いかえれば、辺の長さが三角比を使って次のように書けるということでもあります。

$a = c \times \cos \theta$, $b = c \times \sin \theta$

今回は斜辺が1、すなわち$c = 1$の場合を考えているわけですから、

$\mathrm{BC} = \cos \theta$, $\mathrm{CA} = \sin \theta$

が答えになります。

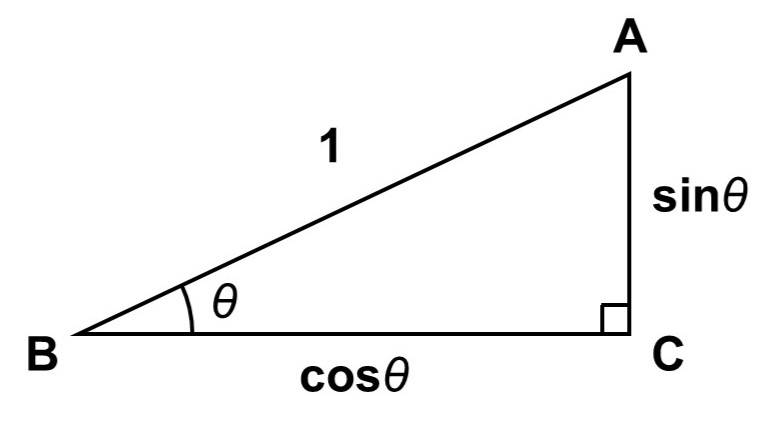
「斜辺を1にしておけば、辺の長さを三角比でそのまま表せる」というのがポイントです。

(2) 直角三角形 → 三角比の流れ

(2)では、二等辺三角形$\mathrm{ABB’}$を使って、2倍角の三角比$\cos 2 \theta$, $\sin 2 \theta$を求めます。二等辺三角形$\mathrm{ABB’}$は(1)の直角三角形から作っているので、辺の長さや内角はわかりますね。

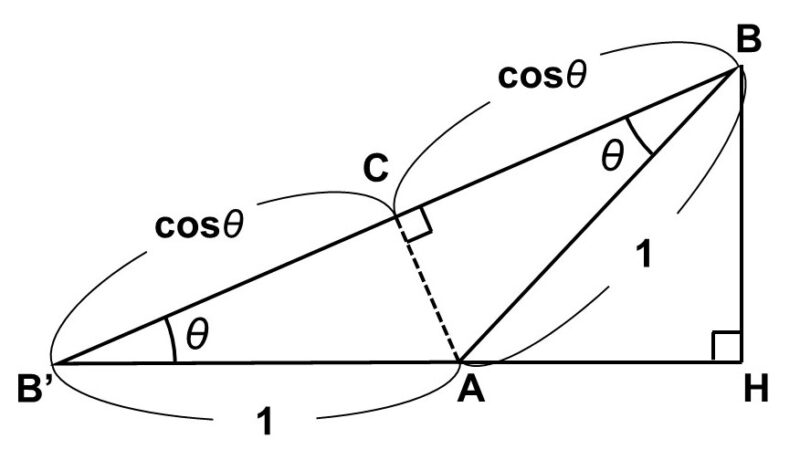
まずは2倍角$2 \theta$がどこにできるか探してみましょう。ここで$\triangle \mathrm{BB’A}$に注目してみると、

$\begin{align}
\angle \mathrm{BAH} &= \angle \mathrm{ABB’}+\angle \mathrm{BB’A} \\[1.5ex]
&= \theta+\theta \\[1.5ex]
&=2 \theta
\end{align}$

であることがわかります（外角の扱い方については30F, T6で解説しています）。

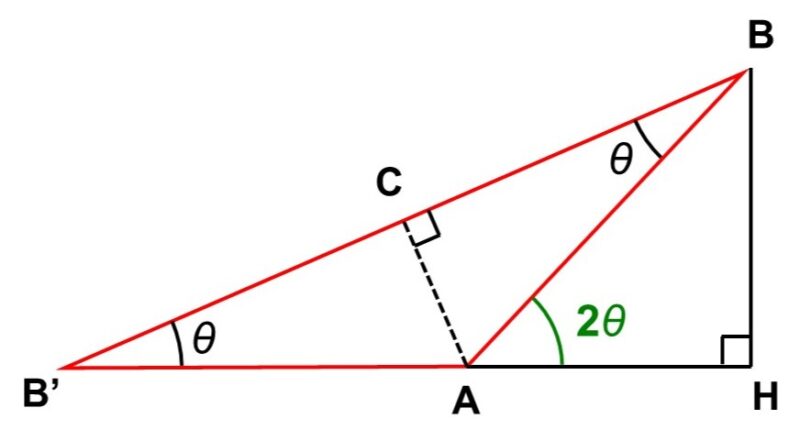
次に、$\cos 2 \theta$, $\sin 2 \theta$を辺の長さに対応させるため、$2 \theta$を内角にもつ直角三角形を探します。ちょうど$\triangle \mathrm{BAH}$が直角三角形であり、斜辺$\mathrm{BA}$の長さは1ですから、(1)と同じように考えれば、

$\mathrm{AH} = \cos 2 \theta$, $\mathrm{HB} = \sin 2 \theta$

となります。

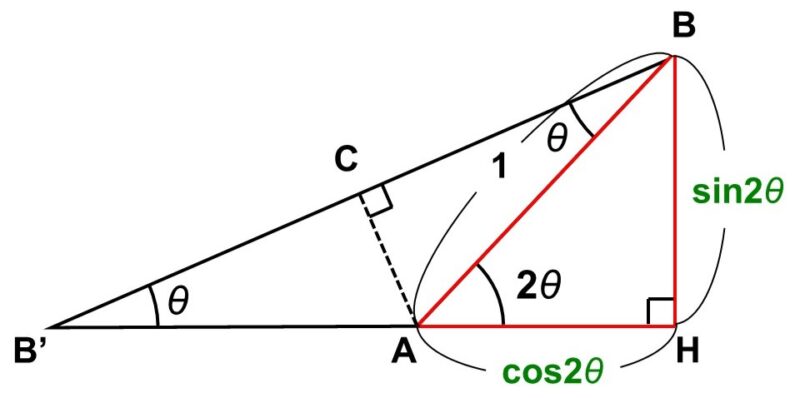
したがって、$\mathrm{AH}$, $\mathrm{HB}$を別の形で表すことができればよいわけです。なので、今度はこの2辺の長さを計算していきましょう。

ここで直角三角形$\mathrm{BB’H}$に注目すると、

$\mathrm{BB’} = 2 \times \mathrm{BC} = 2 \times \cos \theta$

$\angle \mathrm{BB’H} = \theta$

なので、(1)で説明したように、三角比の定義を使って$\mathrm{B’H}$, $\mathrm{HB}$を求めることができます。これ以降は式を見やすくするため、掛け算の記号（×）は省略しますが、

$\mathrm{B’H} = \mathrm{BB’} \cos \theta = 2 \cos^2 \theta$

$\mathrm{HB} = \mathrm{BB’} \sin \theta = 2 \cos \theta \sin \theta$

と計算できます。

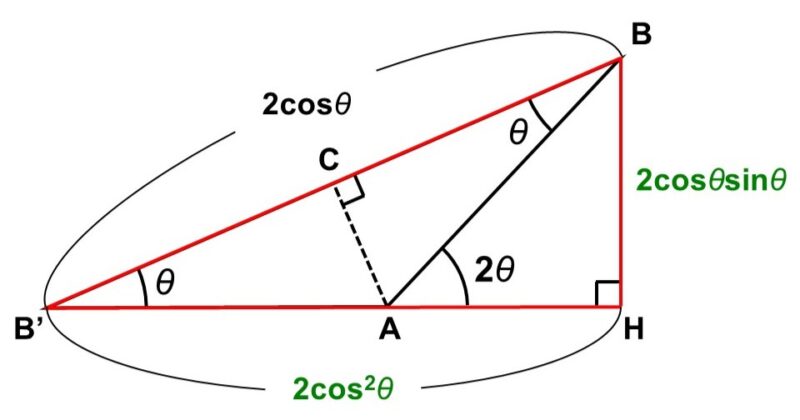
これで$\mathrm{HB}$の方は求まったので、

$\mathrm{HB} = \sin 2 \theta = 2 \cos \theta \sin \theta$

であることがわかりました。

一方、$\mathrm{AH}$の方はというと、先ほど求めた$\mathrm{B’H}$と$\mathrm{B’A} = 1$であることを使えば、

$\begin{align}
\mathrm{AH} &= \mathrm{B’H}-\mathrm{B’A} \\[1.5ex]
&= 2 \cos^2 \theta-1
\end{align}$

と計算できるので、

$\mathrm{AH} = \cos 2 \theta = 2 \cos^2 \theta-1$

となります。

(3) 考え方は(2)と同じでOK

(3)では、二等辺三角形$\mathrm{BAA’}$を使って、$\cos 2 \theta$, $\sin 2 \theta$を求めます。今回は$\angle \mathrm{A’BA}$で$2 \theta$になっていることがすぐにわかりますね。

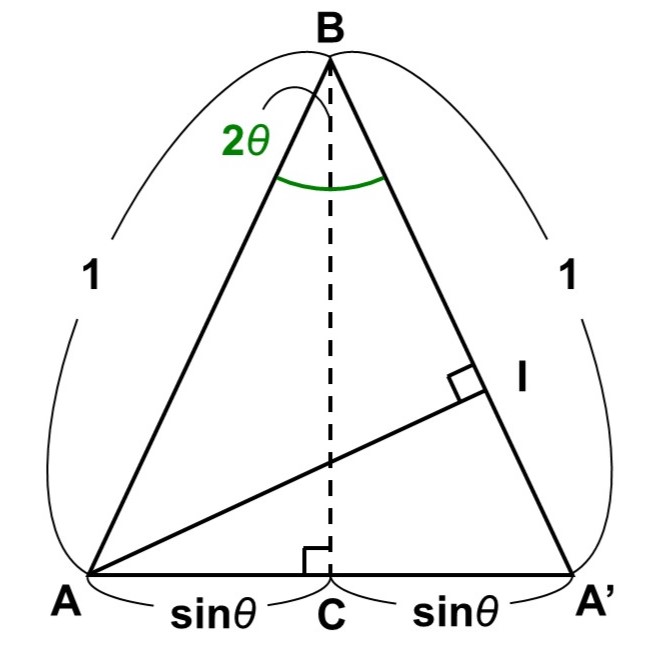
では(2)と同じように、$2 \theta$を内角にもつ直角三角形を探して、辺の長さと$\cos 2 \theta$, $\sin 2 \theta$を対応させましょう。

問題文にあるように、$\triangle \mathrm{BAI}$がまさにその直角三角形であり、斜辺$\mathrm{BA}$の長さも1ですから、

$\mathrm{IB} = \cos 2 \theta$

$\mathrm{AI} = \sin 2 \theta$

となります。

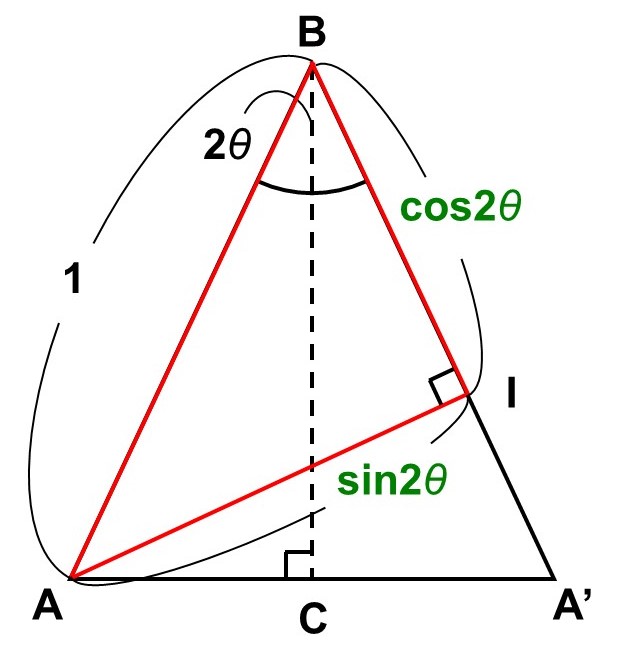
続いて、この2辺を別の形で表せるように計算していきます。ここで、となりにある直角三角形$\mathrm{AA’I}$に注目すると、

$\angle \mathrm{AA’I} = \angle \mathrm{CA’B} = 90^{\circ}-\theta$

であり、余角にあたる$\angle \mathrm{IAA’}$は$\theta$です。つまり、$\triangle \mathrm{AA’I} (\triangle \mathrm{A’AI})$は元の直角三角形$\triangle \mathrm{ABC}$と相似ということになります。

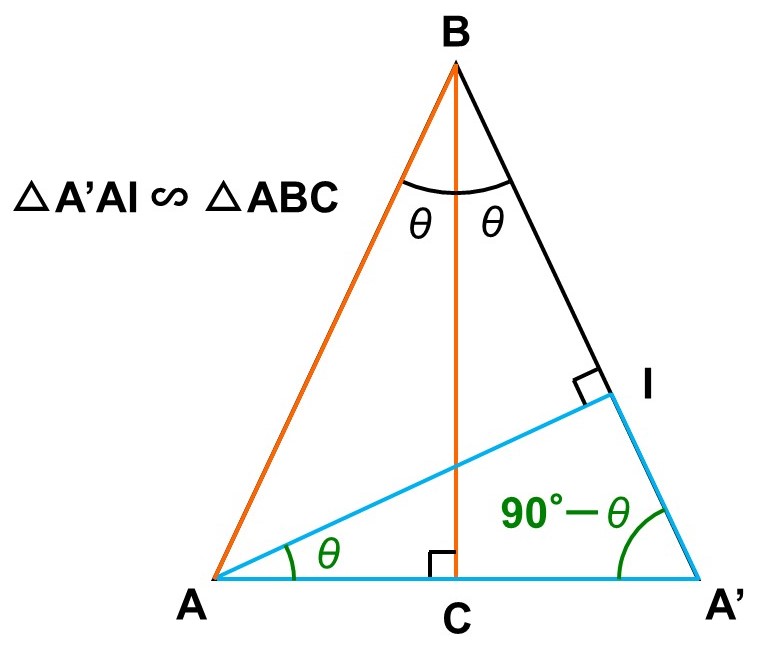
したがって$\triangle \mathrm{AA’I}$は、斜辺が$\mathrm{AA’} = 2 \sin \theta$、角度が$\theta$の直角三角形と見ることができるので、

$\mathrm{IA} = \mathrm{AA’} \cos \theta = 2 \sin \theta \cos \theta$

$\mathrm{A’I} = \mathrm{AA’} \sin \theta = 2 \sin^2 \theta$

と表せます。

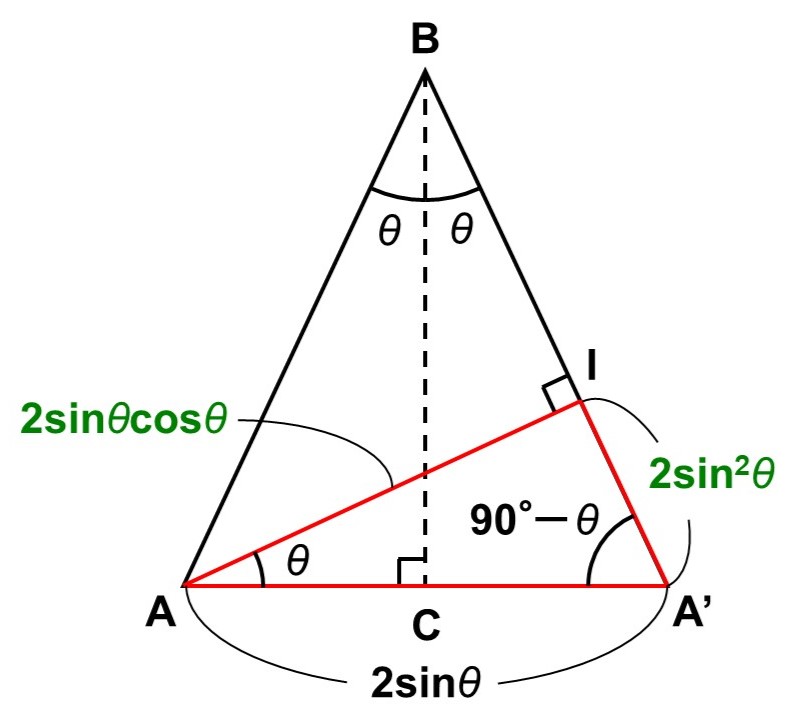
これで$\mathrm{AI}$の方はできあがりました。

$\mathrm{AI} = \sin 2 \theta = 2 \sin \theta \cos \theta$

一方、$\mathrm{IB}$の方は、今求めた$\mathrm{A’I}$と$\mathrm{A’B} = 1$を使えば、

$\begin{align}
\mathrm{IB} &= \mathrm{A’B}-\mathrm{A’I} \\[1.5ex]
&= 1-2\sin^2 \theta
\end{align}$

と表せますから、

$\mathrm{IB} = \cos 2 \theta = 1-2\sin^2 \theta$

となります。

(4) cosとsinにかくされた関係とは？

(2), (3)の結果を見比べてみると、$\cos 2 \theta$の方は答えが少し異なることがわかります。ですが、どちらかが間違っているわけではありません。

実は$\cos \theta$と$\sin \theta$の間には、2つをつなぐ次のような関係式があります。

$\cos^2 \theta+\sin^2 \theta = 1$

この関係式は(2), (3)の結果からも導くことができます。(2), (3)の結果によれば、次の等式が成り立ちます。

$2 \cos^2 \theta-1 = 1-2 \sin^2 \theta$

等式というのは、文字どおり「等しい」ことを表す式です。したがって、両辺に対して「同じこと」を行う分には＝が保たれます。

そこでまず、両辺に1を足してみます。

$\begin{align}
&\hspace{30pt} (2 \cos^2 \theta-1)+1 = (1-2\sin^2 \theta)+1 \\[1.5ex]
&\iff \hspace{5pt} 2 \cos^2 \theta = 2-2 \sin^2 \theta
\end{align}$

左辺が少し見やすくなりました。次に、両辺に$2 \sin^2 \theta$を足してみます。

$\begin{align}
&\hspace{32pt} 2 \cos^2 \theta+2 \sin^2 \theta = (2-2 \sin^2 \theta)+2 \sin^2 \theta \\[1.5ex]
&\iff \hspace{5pt} 2 \times (\cos^2 \theta+\sin^2 \theta) = 2
\end{align}$

右辺も見やすくなりました。最後に、両辺を2で割ってみます。

$\begin{align}
&\hspace{30pt} \dfrac{2 \times (\cos^2 \theta+\sin^2 \theta)}{2}= \dfrac{2}{2} \\[1.5ex]
&\iff \hspace{5pt} \cos^2 \theta+\sin^2 \theta = 1
\end{align}$

このようにして、$\cos \theta$と$\sin \theta$の関係式を導くことができます。

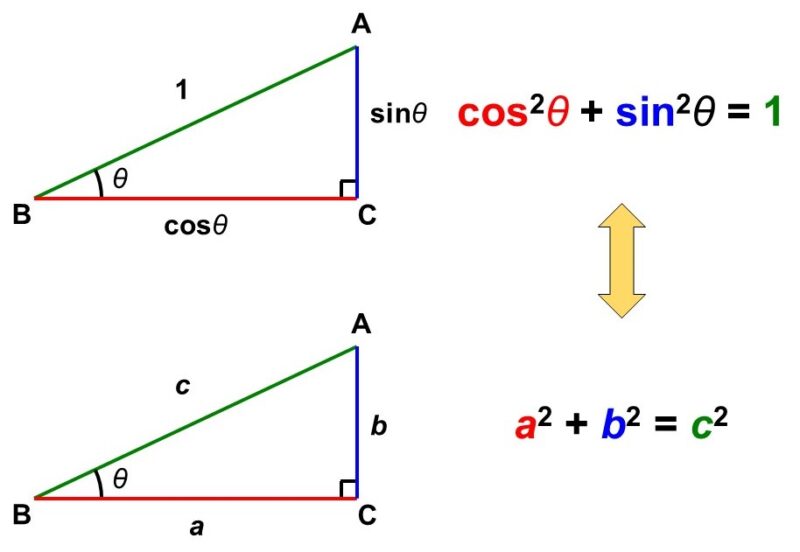
この$\cos \theta$と$\sin \theta$の関係式の意味を少し考えてみましょう。$\cos \theta$, $\sin \theta$の定義は次のようになっていました。

つまり、$\cos^2 \theta+\sin^2 \theta = 1$という式は、次のように書くこともできます。

$\begin{align}
&\hspace{30pt} (\dfrac{a}{c})^2+(\dfrac{b}{c})^2 = 1 \\[1.5ex]
&\iff \hspace{5pt} \dfrac{a^2}{c^2}+\dfrac{b^2}{c^2} = 1
\end{align}$

等式においては「同じこと」をしても＝が保たれるので、両辺に$c^2$を掛けてみます。

$\begin{align}
&\hspace{30pt} (\dfrac{a^2}{c^2}+\dfrac{b^2}{c^2}) \times c^2 = 1 \times c^2 \\[1.5ex]
&\iff \hspace{5pt} \dfrac{a^2}{c^2} \times c^2+\dfrac{b^2}{c^2} \times c^2 = c^2 \\[1.5ex]
&\iff \hspace{5pt} a^2+b^2 = c^2
\end{align}$

これは直角三角形における重要な式で、三平方の定理（ピタゴラスの定理）と呼ばれています。すなわち、「斜辺の2乗は残り2辺それぞれの2乗の和に等しい」ということです。

最後に、今回出てきた重要な公式をまとめておきます。32F時点では、これらを使いこなせるレベルにはないので、いずれについてもまた別の機会でくわしくお話しします。