今回の問題は全部で3問あります。（※34Fまでの内容を理解していることが前提です！）
※以下の問いでは、円周率を$\pi \fallingdotseq 3.14$として計算しなさい。
円の一部を切り取った図形は、その形から扇形（おうぎがた）と呼ばれていて、例えば次のa, bのようなものがある。
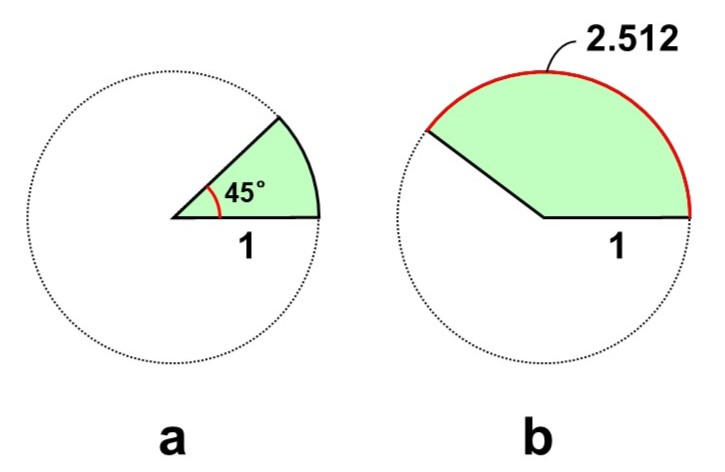
扇形は、1. 半径と2. 中心角（aの赤線部分）あるいは弧の長さ（bの赤線部分）の2つがわかっていれば、元の円に対する比率を考えることで面積を計算することができる。
(1) 扇形a, bの面積を求めなさい。
扇形をうまく利用すると、次のような少し変わった図形の面積の計算もできる。
（例1）
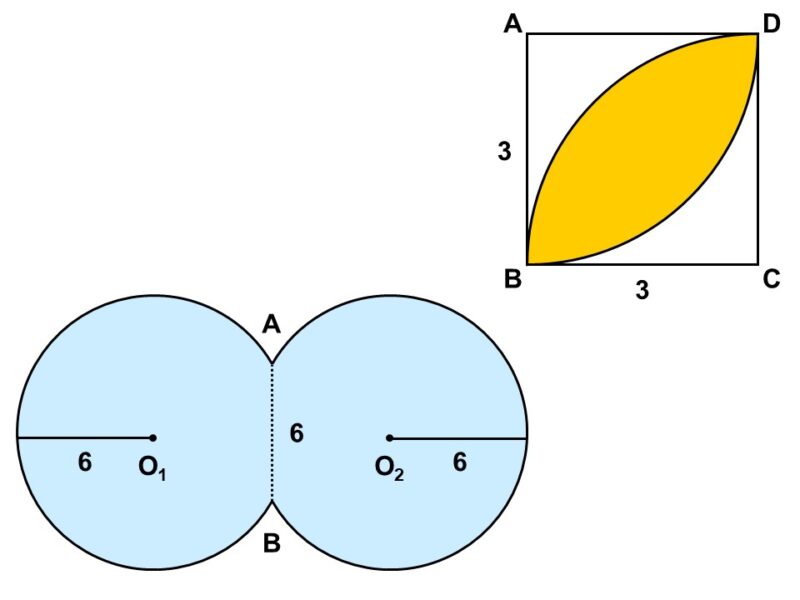
1辺の長さが3の正方形$\mathrm{ABCD}$がある。ここで、$\mathrm{A}$, $\mathrm{C}$を中心とした半径3の円を描くと、正方形の中にオムレツのような図形$\mathrm{BD}$ができた。
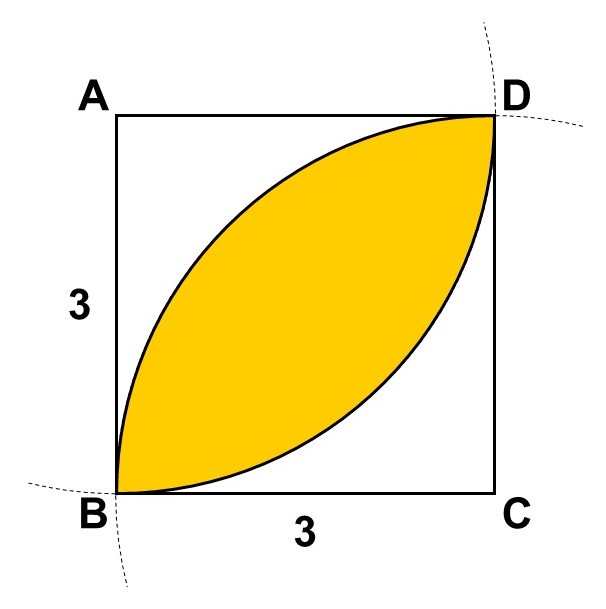
(2) 図形$\mathrm{BD}$の面積を求めなさい。
（例2）
半径2の円$\mathrm{O_1}$, $\mathrm{O_2}$を重ね合わせると、団子のような図形$\mathrm{O_1O_2}$が作れるが、実は空気中の窒素分子や酸素分子もこのような形をしていることが知られている。
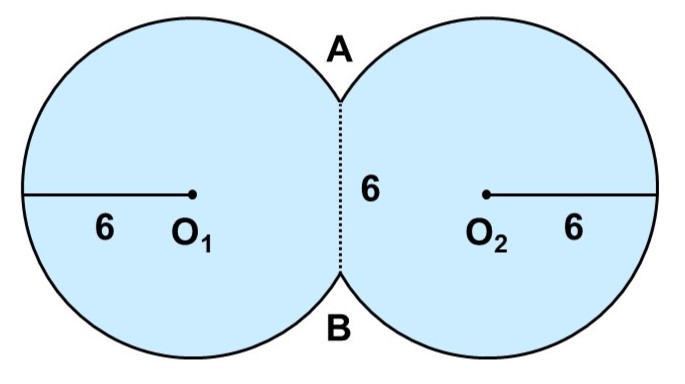
(3) 図形$\mathrm{O_1O_2}$の面積を求めなさい。必要であれば$\cos30^{\circ} \fallingdotseq 0.866$を用いてもよい。
円の一部である扇形は、空間図形の1つ「円錐（えんすい）」を切り開いた時にもあらわれる重要な図形です。今回の問題を通して、扇形の扱いに慣れておきましょう。
(1) 扇形の基本は「比率」の考え方
まずは(1)で扇形の基本を理解していきます。
扇形は円の一部なので、その面積は「元の円に対してどれだけの割合を占めるのか？（＝比率）」を考えることで計算できます。
扇形aは中心角がわかっている場合です。
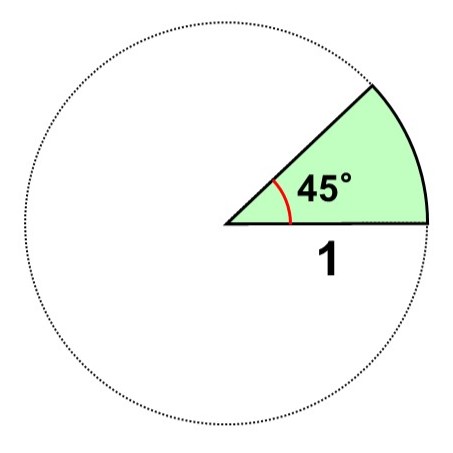
中心角を使って比率を考える場合は、分母を360°にして計算します。
$(3.14 \times 1^2) \times \dfrac{45}{360} = 0.3925$
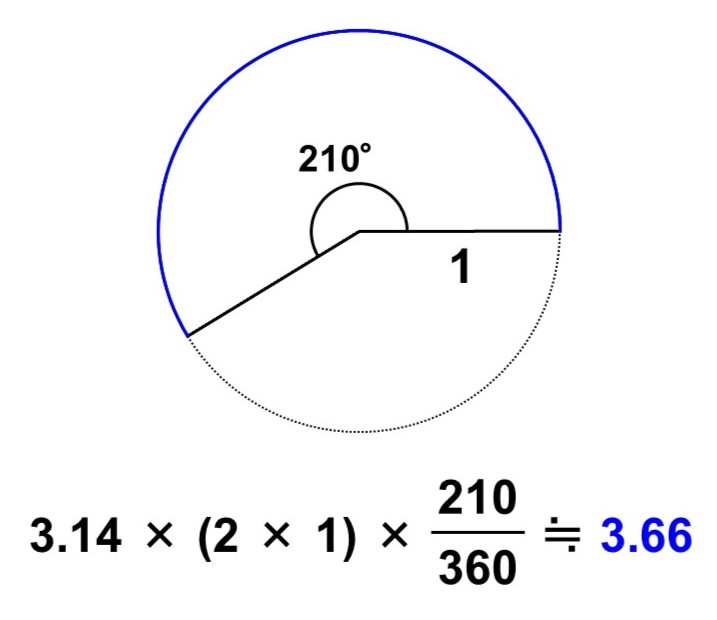
扇形bは弧の長さがわかっている場合です。
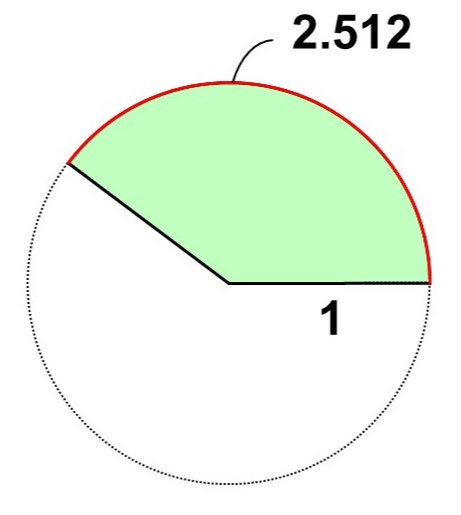
弧の長さを使って比率を考える場合は、分母を円周の長さにして計算します。元の円の周の長さは$3.14 \times (2 \times 1) = 6.28$なので、
$(3.14 \times 1^2) \times \dfrac{2.512}{6.28} = 1.256$
今回は面積の話をメインでしていますが、扇形の弧の長さについても、中心角から比率を考えることで計算できます。
（例）
(2) 扇形の中に三角形を見つけ出せ！
(2)は扇形を使った応用問題です。扇形をうまく使うと、実はこんなオムレツみたいな図形の面積も求めることができてしまいます。
ところで、この図形$\mathrm{BD}$を見た時、初めに必ず注目したい点があります。それは線対称な図形だということです。次のように、対角線$\mathrm{BD}$がそのまま対称軸になっています。
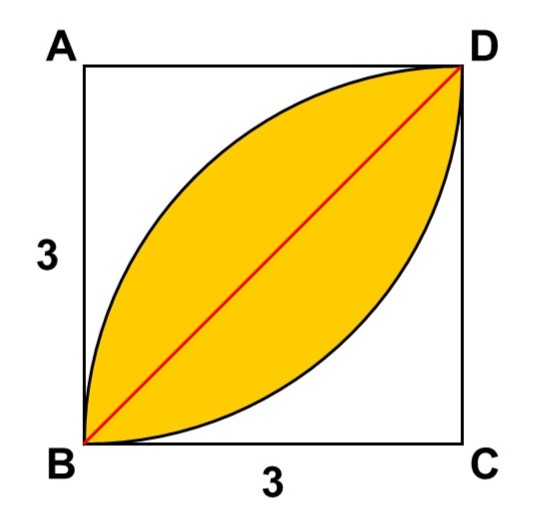
これはすなわち、対称軸をはさんで左半分と右半分で面積が同じということを意味しています。なので、左か右のどちらかの面積を求めて2倍すればこの図形の面積が求まります。今回は左半分（図形$\mathrm{bd}$と呼ぶことにします）に注目して計算してみましょう。
図形$\mathrm{bd}$は三角形でも四角形でも円でもないので、一見すると面積を求めるのが難しいように思えます。しかし、対角線を入れた先ほどの図を改めて見てみると、この図形は扇形から直角二等辺三角形がくり抜かれてできていることに気がつきます。
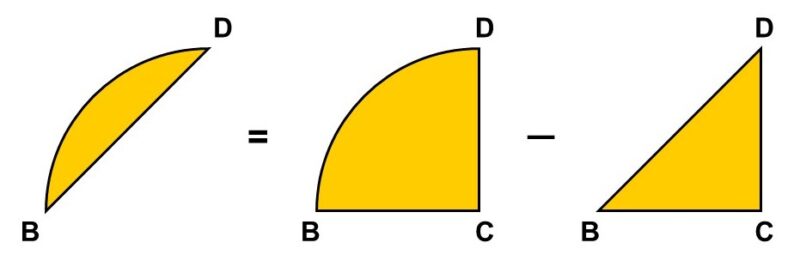
したがって、扇形$\mathrm{BCD}$と直角三角形$\mathrm{BCD}$をそれぞれ求め、最後に差し引けば、図形$\mathrm{bd}$の面積はあっさり求まってしまいます。
扇形$\mathrm{BCD}$は、半径が3、中心角が90°なので、その面積は
$(3.14 \times 3^2) \times \dfrac{90}{360} = 7.065$
となります。一方、直角二等辺三角形$\mathrm{BCD}$の面積は
$\dfrac{3 \times 3}{2} = 4.5$
なので、図形$\mathrm{bd}$の面積は
$7.065-4.5 = 2.565$
となります。もともと求めたかった面積はこれを2倍したものですから、
$2.565 \times 2 = 5.13$
が答えになります。
(3)は(2)と同じように考えればOK
(3)は2つの円を重ねたような図形です。(2)が理解できたのであれば、そこまで難しくないはずです。
(2)と同じく(3)も線対称な図形であり、対称軸$\mathrm{AB}$を持っています。
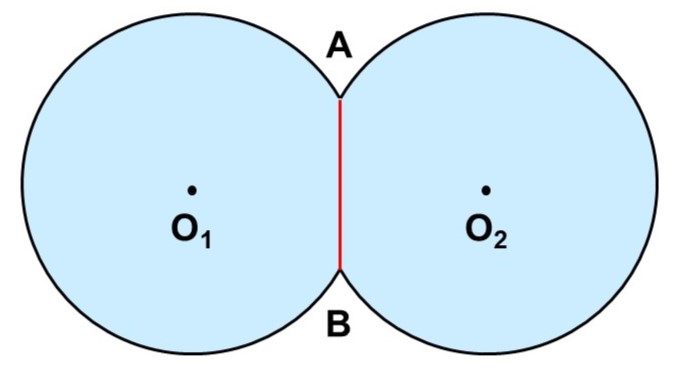
つまり、左半分か右半分の面積を求めて2倍すれば、図形$\mathrm{O_1O_2}$の面積となります。ここでは左半分（図形$\mathrm{O_{1}}$と呼ぶことにします）に注目してみます。
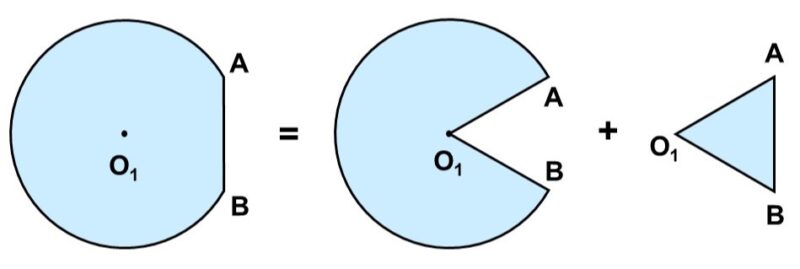
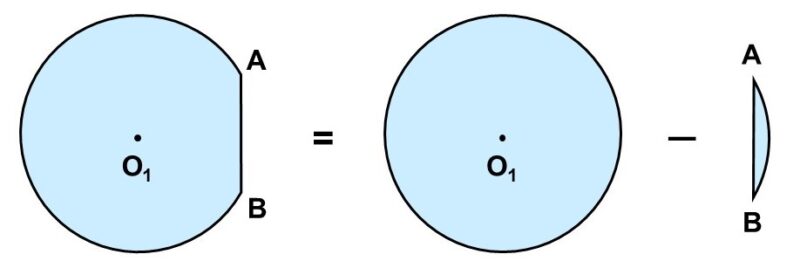
図形$\mathrm{O_{1}}$は円の一部が欠けたような形をしています。したがって、欠けた部分（図形$\mathrm{AB}$）の面積を求め、元の円の面積から差し引けば面積がわかります。
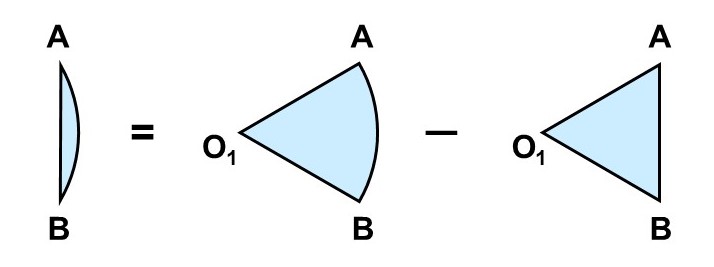
図形$\mathrm{AB}$の面積はというと、これは(2)で経験済みですね。対応する扇形$\mathrm{AO_{1}B}$から$\triangle \mathrm{AO_{1}B}$を切り取ることで求まります。
ここで先に$\triangle \mathrm{AO_{1}B}$に注目してみると、$\mathrm{AB} = 6$、円$\mathrm{O_{1}}$の半径が6（$\mathrm{O_{1}A} = \mathrm{O_{1}B} = 6$）であることから、これは正三角形であることがわかります。よって、中心角$\angle \mathrm{AO_{1}B}$はちょうど60°となります。
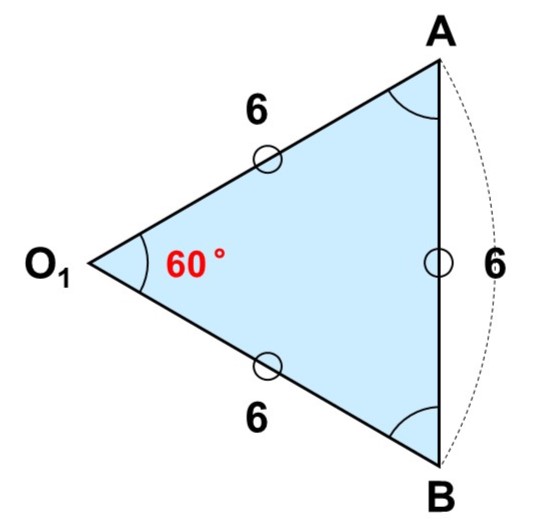
これより、扇形$\mathrm{AO_{1}B}$の面積は
$(3.14 \times 6^2) \times \dfrac{60}{360} = 18.84$
と計算できます。
正三角形$\mathrm{AO_{1}B}$の面積も求めましょう。$\mathrm{AB}$を「底辺」と見て、頂点$\mathrm{O_{1}}$から垂線$\mathrm{O_{1}H}$を下ろしてみると、これが「高さ」になるわけですが、一方で二等辺三角形の性質から$\angle \mathrm{AO_{1}H} = \angle \mathrm{BO_{1}H} = 30^{\circ}$、$\mathrm{AH} = \mathrm{BH} = 3$となっていることがわかります。
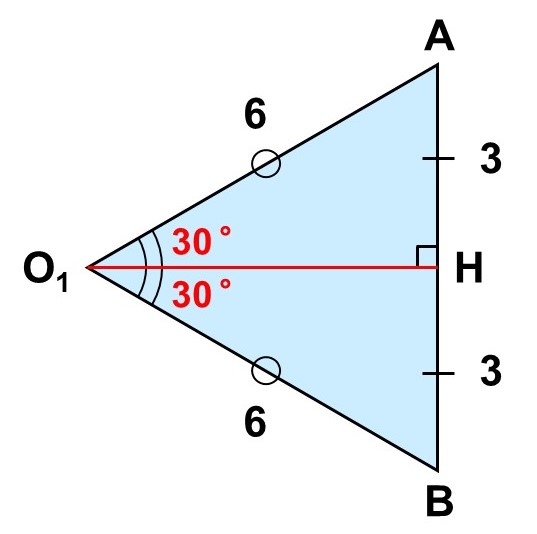
よって、直角三角形$\mathrm{AO_{1}H}$で三角比を考えてあげることで、$\mathrm{O_{1}H}$を求めることができます。
$\begin{align}
\mathrm{O_{1}H} &= \mathrm{AO_{1}} \times \cos30^{\circ} \\[1.5ex]
&\fallingdotseq 6 \times 0.866 \\[1.5ex]
&= 5.196
\end{align}$
ゆえに、正三角形$\mathrm{O_{1}AB}$の面積は
$\dfrac{6 \times 5.196}{2} = 15.588$
となります。
以上から、図形$\mathrm{AB}$の面積は
$18.84-15.588 = 3.252$
となるので、図形$\mathrm{O_{1}}$の面積は
$(3.14 \times 6^2)-3.252 = 109.788$
と計算でき、もともと求めたかった図形$\mathrm{O_1O_2}$の面積は
$109.788 \times 2 = 219.576$
となります。
図形$\mathrm{O_{1}}$の求め方としては、次のように扇形と正三角形に分ける方法も考えられます。
この場合、扇形$\mathrm{AO_{1}B}$の面積は
$(3.14 \times 6^2) \times \dfrac{360-60}{360} = 94.2$
と計算でき、図形$\mathrm{O_{1}}$の面積は
$94.2+15.588 = 109.788$
と正しく求めることができます。こちらの方がシンプルですね。
幾何学（初等幾何）におけるあらゆる平面図形は、三角形と円の組合せで考えることができるので、扇形まで扱えるようになれば、基本的にはすべての図形について、その面積が計算できるようになったと言えます。
あとは、いろんな図形に出会いながら「三角形や円をどう組み合わせたらその図形になるか」を考えるトレーニングをしていけば、あなたもきっと平面図形マスターになれるはずです！
