今回の問題は全部で3問あります。(※35Fまでの知識が前提です!)
大きさのある物体は、その物体の重さを代表する点となる重心(じゅうしん)をもっている。
例えば、重さが無視できる軽い棒の両端に20 gの重りと10 gの重りをつけると、重心となる点で系全体が重さの逆比(この場合は20gの重りの方から1 : 2)に内分されることが知られている。
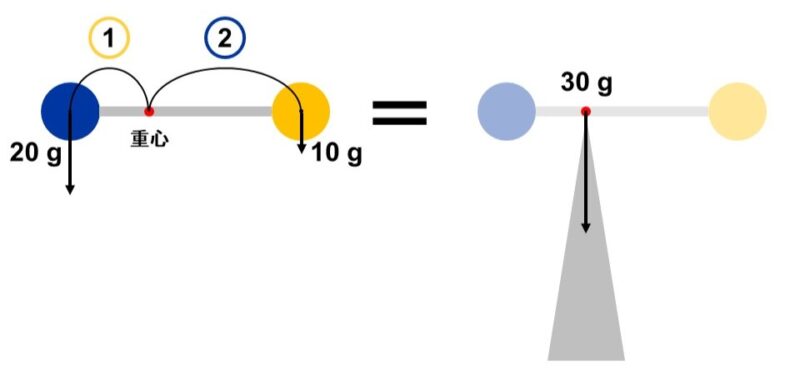
すなわち、系全体の重さは赤い点にのみかかっているとみなすことができ、その点を支えるだけで棒は倒れずに安定する。
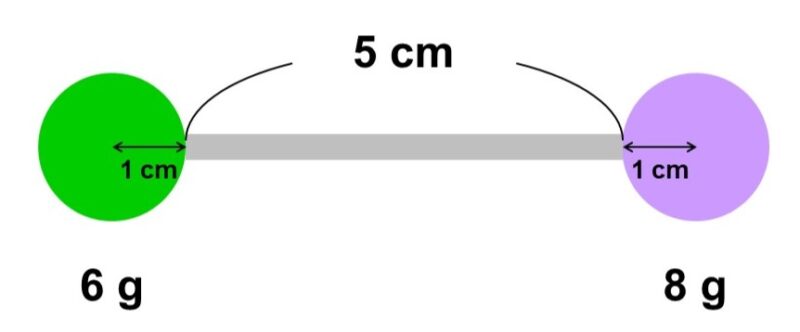
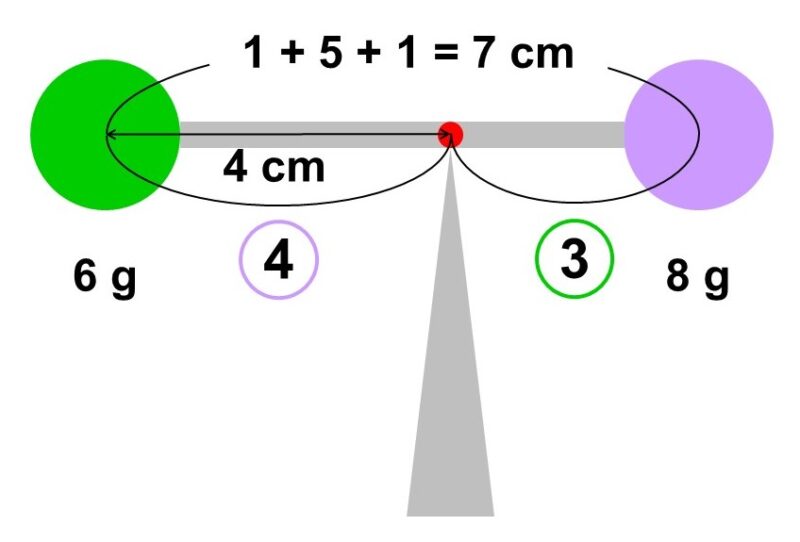
(1) 図のように、重さが無視できる軽い棒(5 cm)の両端に6 gと8 gの重り(半径1 cmの球)をとりつけた。この物体の重心はどこにあるか求めなさい。
「重心」は平面図形においても定義することができる。
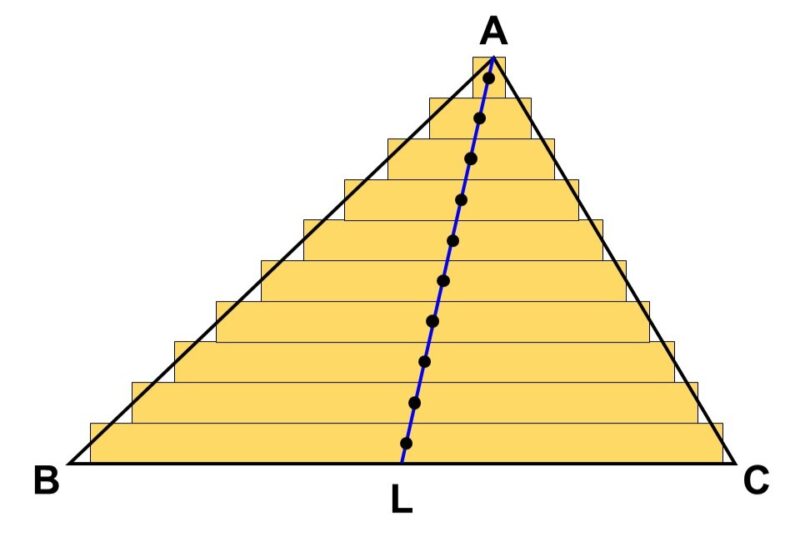
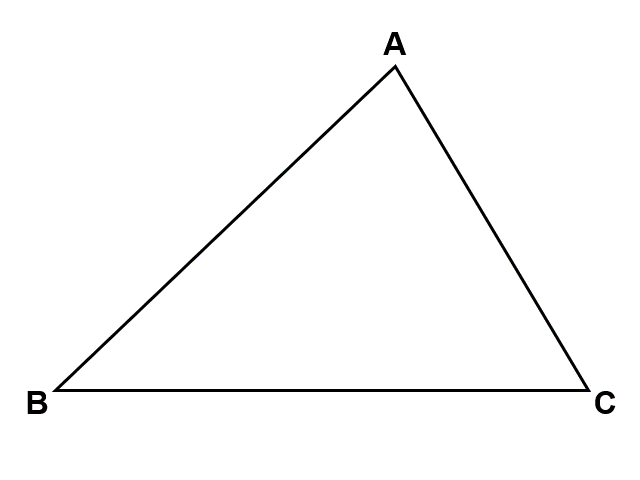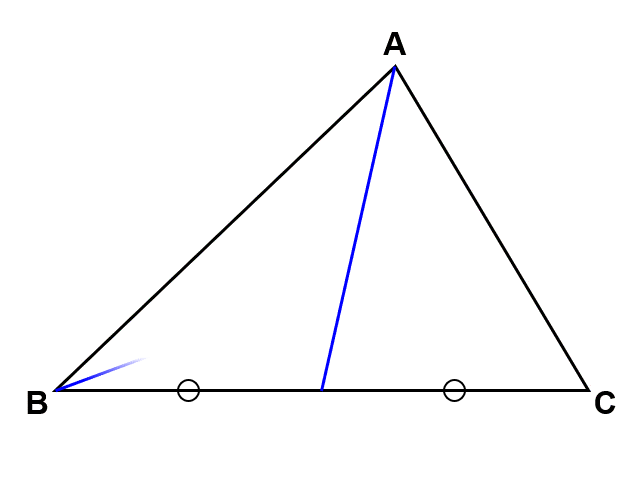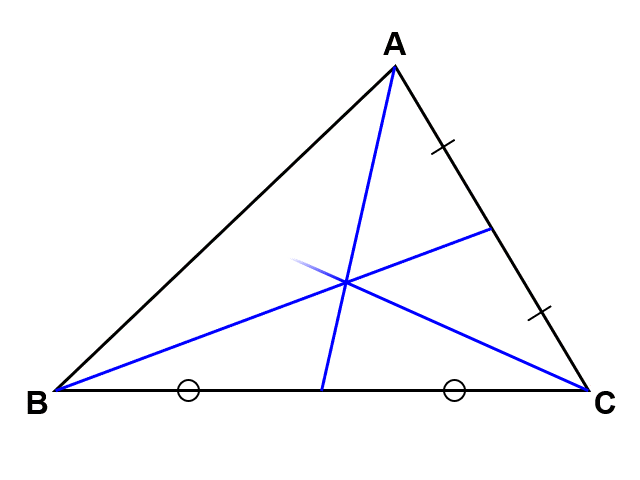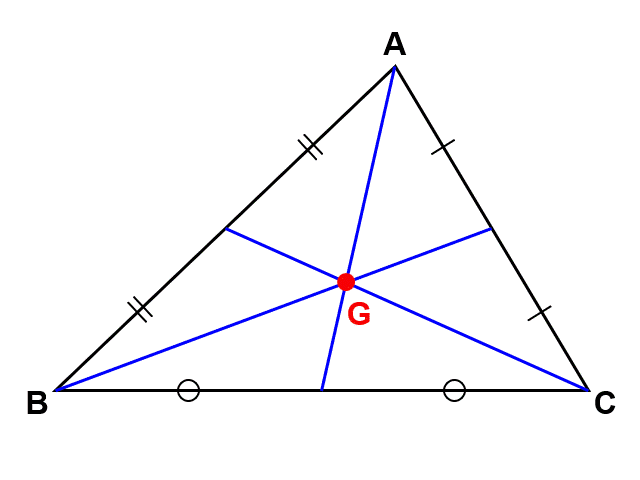
三角形において、各頂点から対辺の中点に向かって線を引く(これを中線という)。すると、これらは必ず1点で交わり、その交点は三角形の重心と呼ばれる(「重力」の英語Gravityの頭文字Gで表す)。
棒の場合と同じく、三角形の重さ(平面図形そのものに重さはないので、ここでは三角形のうすい板をイメージ)は重心にのみかかっているとみなすことができ、この点を支えれば三角形は倒れずに安定する。
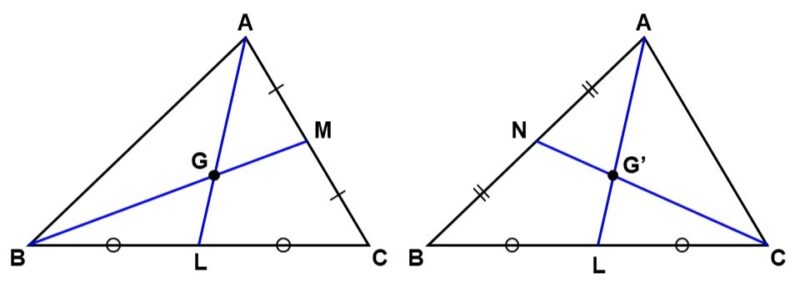
(2) 三角形の各頂点から引いた中線が1点で交わることは、中線$\mathrm{AL}$, $\mathrm{BM}$の交点を$\mathrm{G}$、中線$\mathrm{AL}$, $\mathrm{CN}$の交点$\mathrm{G’}$とした時、この2点が同じであることを示せば証明できる。
これをふまえ、3本の中線が1点で交わることを証明しなさい。
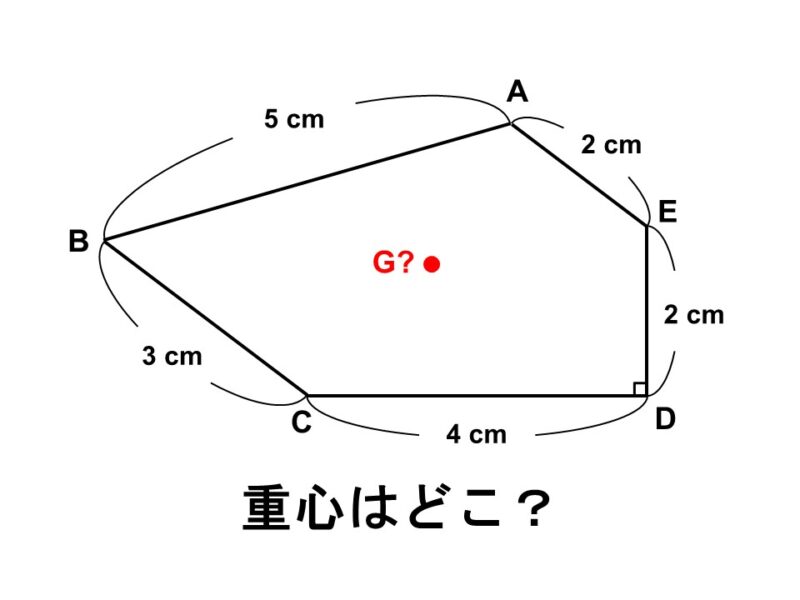
(3) 厚さが無視できるうすい板(1 cm2あたり1 g)があり、この板から次のような五角形を切り出した。
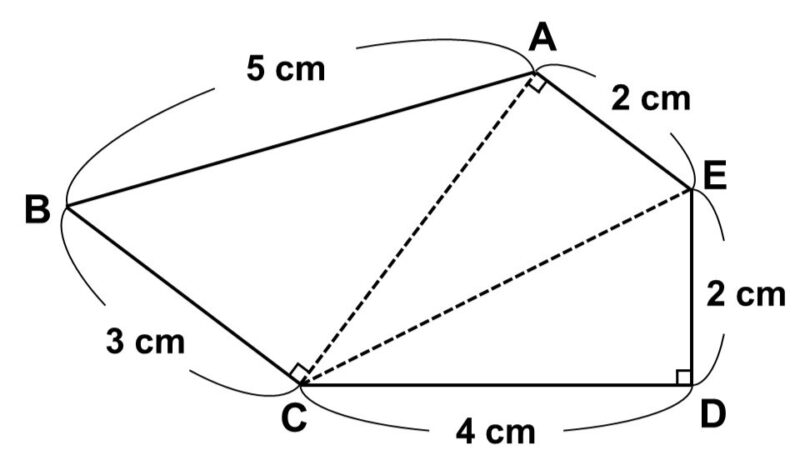
この五角形の重心はどこにあるか求めなさい。
三角形には内心・傍心(35F)、外心・垂心(36F)とならんで重心と呼ばれるものがあり、これらは三角形の五心として知られています。
「重心」は物理で本格的に登場する概念ですが、日常生活にも役立つ大切な考え方がかくれています。この問題を通して、「重心」についての理解を深めていきましょう!
(1) 重心を見つけよう

(1)は重心の見つけ方を理解するための問題です。
例にあったように、重心によって系全体は重さの逆比に内分されます。今回の場合、一方の重りの中心からもう一方の重りの中心までの距離は1 + 5 + 1 = 7 cmなので、60 gの重りの中心から80 : 60 = 4 : 3に内分する点、すなわち60 gの重りの中心から4 cmのところに重心があります。
(2) ポイントは「相似」

(2)は証明問題です。あらかじめヒントは出しておきましたが、少し難しかったかもしれません。
方針としては、$\mathrm{G}$と$\mathrm{G’}$がどちらも線分$\mathrm{AL}$を同じように内分していることを示していきます[1]。
また、今回は複数の中点が登場しているので、中点連結定理(相似)を利用することができます。
(証明)
中点$\mathrm{L}$, $\mathrm{M}$を結ぶ。
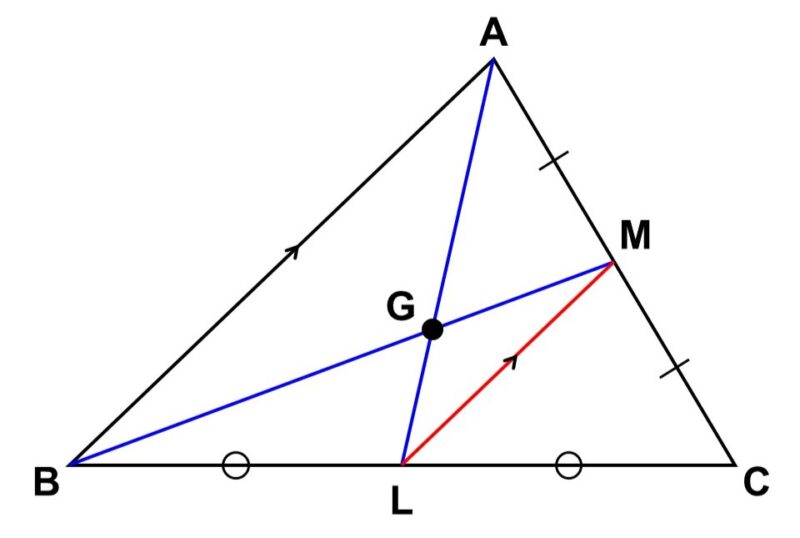
すると、中点連結定理($\triangle \mathrm{CAB}$ ∽ $\triangle \mathrm{CML}$)から
$\mathrm{AB} /\!/ \mathrm{ML}$ <1>
$\mathrm{AB} : \mathrm{ML} = 2 : 1$ <2>
よって、<1>から錯角が等しく、
$\angle \mathrm{GAB} = \angle \mathrm{GLM}$ <3>
$\angle \mathrm{ABG} = \angle \mathrm{LMG}$ <4>
<3>, <4>から、$\triangle \mathrm{ABG}$と$\triangle \mathrm{LMG}$は、2つの角がそれぞれ等しいので相似である。
したがって対応する辺の比は等しく、<2>から
$\begin{align}
\mathrm{AG} : \mathrm{GL} &= \mathrm{AB} : \mathrm{LM} \\[1.5ex]
&= 2 : 1
\end{align}$
つまり、交点$\mathrm{G}$は線分$\mathrm{AL}$を2 : 1に内分する。
つづいて、中点$\mathrm{L}$, $\mathrm{N}$を結ぶ。
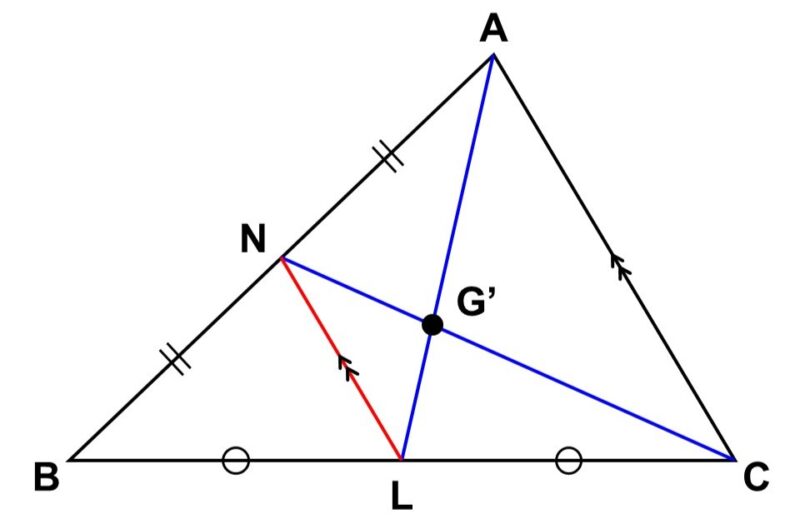
すると、中点連結定理($\triangle \mathrm{BCA}$ ∽ $\triangle \mathrm{BLN}$)より、
$\mathrm{CA} /\!/ \mathrm{LN}$ <5>
$\mathrm{CA} : \mathrm{LN} = 2 : 1$ <6>
よって、<5>から錯角が等しく、
$\angle \mathrm{G’CA} = \angle \mathrm{G’NL}$ <7>
$\angle \mathrm{CAG’} = \angle \mathrm{NLG’}$ <8>
<7>, <8>から、$\triangle \mathrm{CAG’}$と$\triangle \mathrm{NLG’}$は、2つの角がそれぞれ等しいので相似である。
したがって対応する辺の比は等しく、<6>から
$\begin{align}
\mathrm{AG’} : \mathrm{G’L} &= \mathrm{CA} : \mathrm{NL} \\[1.5ex]
&= 2 : 1
\end{align}$
つまり、交点$\mathrm{G’}$は線分$\mathrm{AL}$を2 : 1に内分する。
以上より、$\mathrm{G}$, $\mathrm{G’}$はどちらも線分$\mathrm{AL}$を2 : 1に内分するので、同じ点である。
すなわち、3本の中線$\mathrm{AL}$, $\mathrm{BM}$, $\mathrm{CN}$はただ一つの点$\mathrm{G}$($\mathrm{G’}$)で交わる。
(証明終)
(3) (1), (2)で学んだことを使おう

(3)では、(1), (2)で学んだことを使って、多角形の重心を求めていきます。
この五角形は3つの直角三角形からできているので、まずは各三角形の重心と重さを求めます。
(2)の証明からもわかるように、三角形の重心は少なくとも2本の中線があれば求まります。また、今回は「1 cm2あたり1 g」という条件があるので、面積がわかればそのまま重さもわかります。
- 直角三角形$\mathrm{CDE}$
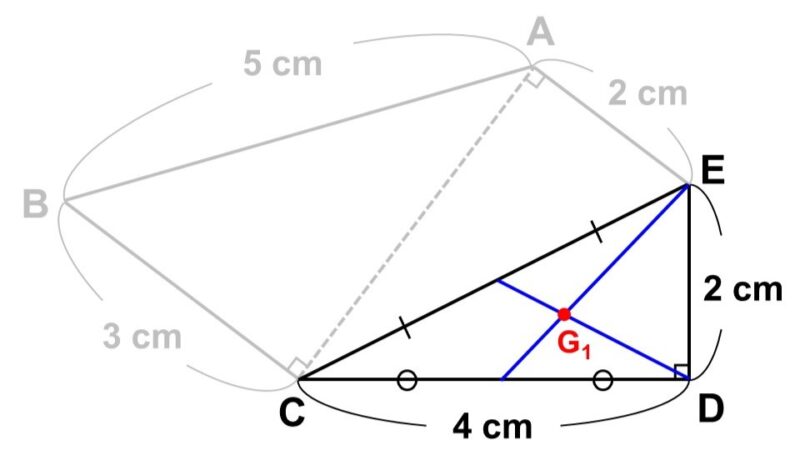
底辺が4 cm、高さが2 cmなので、面積は
$\dfrac{4 \times 2}{2} = 4$ cm2
つまり、重心$\mathrm{G_1}$に4 gの重さがかかっていると考えられます。
- 直角三角形$\mathrm{CAE}$
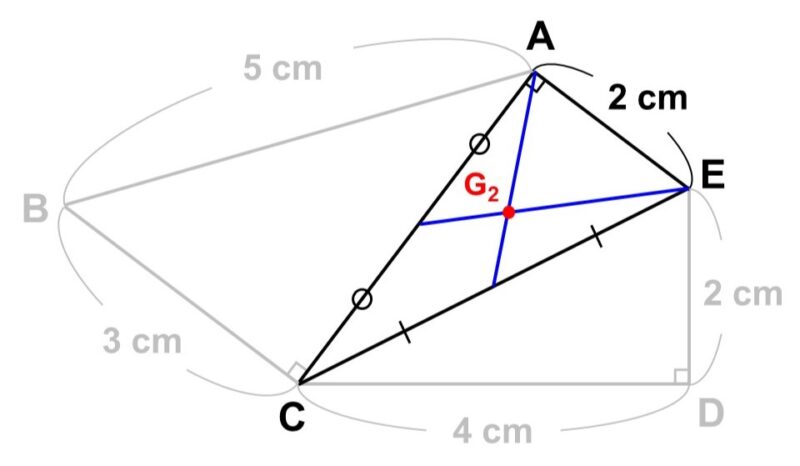
この直角三角形は、底辺となる$\mathrm{CA}$の長さがあたえられていません。ですが、これはすぐにわかります。というのも、直角三角形$\mathrm{CDE}$と合同だからです。
すなわち、
- $\mathrm{EC}$が共通
- $\mathrm{AE} = \mathrm{DE} = 2$ cm
なので、直角三角形の合同条件「斜辺と他の1辺がそれぞれ等しい」をみたしています。
したがって対応する辺は等しく($\mathrm{CA} = \mathrm{CD}$)、$\mathrm{CA}$は4 cmとわかります。
ただ、合同とわかれば面積の計算はもう必要ありませんね。重さは直角三角形$\mathrm{CDE}$と同じく4 gであり、これが重心$\mathrm{G_2}$にかかっています。
- 直角三角形$\mathrm{ABC}$
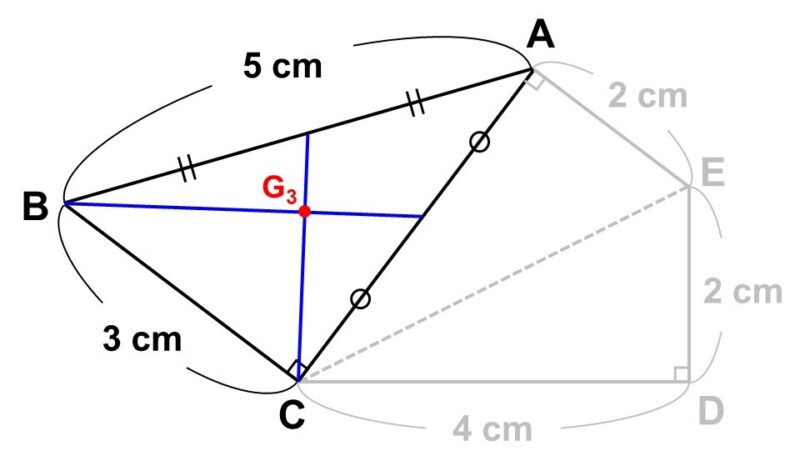
$\mathrm{BC}$(3 cm)を底辺と見ると、高さ$\mathrm{CA}$の長さが4 cmであることは先ほど確認したので、面積は
$\dfrac{3 \times 4}{2} = 6$ cm2
つまり、重心$\mathrm{G_3}$には6 gの重さがかかっていると考えられます。
以上で各三角形についての重心と重さはわかりました。
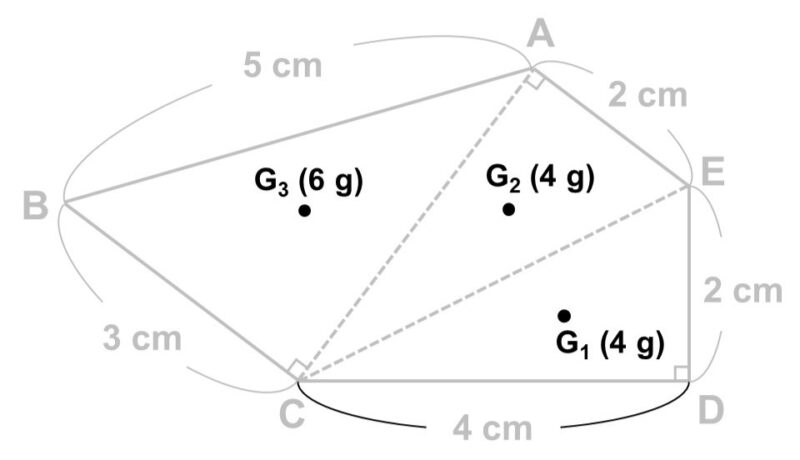
あとはこの3点のみに注目し、(1)で学んだことを使って図形全体の重心を決めていきます。
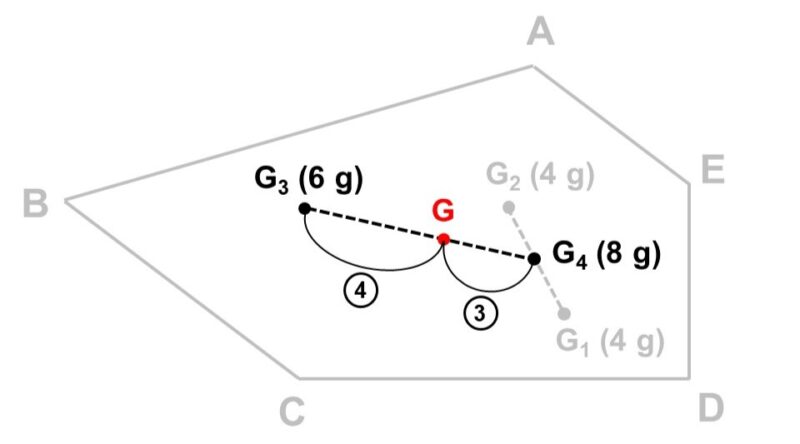
まず、線分$\mathrm{G_1} \mathrm{G_2}$を考えます。$\mathrm{G_1}$, $\mathrm{G_2}$には同じ4 gの重さがかかっているので、ちょうど中点(1 : 1に内分する点)が重心$\mathrm{G_4}$となります。
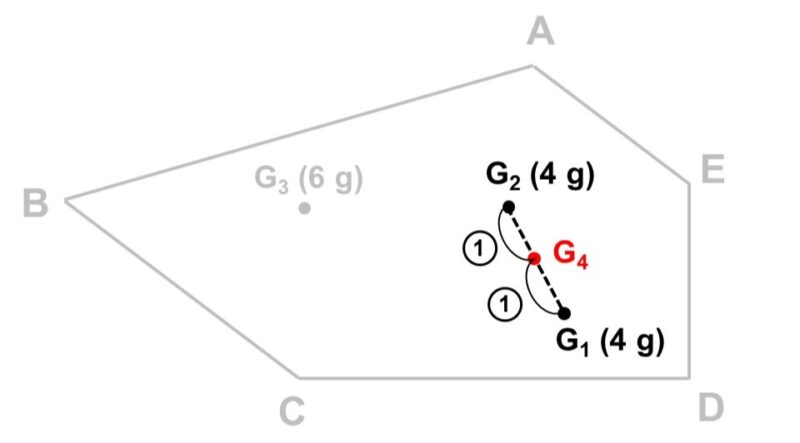
次に、線分$\mathrm{G_3} \mathrm{G_4}$を考えます。$\mathrm{G_3}$には6 g、$\mathrm{G_4}$には4 + 4 = 8 gの重さがかかっているので、重さの逆比、すなわち$\mathrm{G_3}$から4 : 3に内分する点が求める重心$\mathrm{G}$となります。
おまけ(実験)
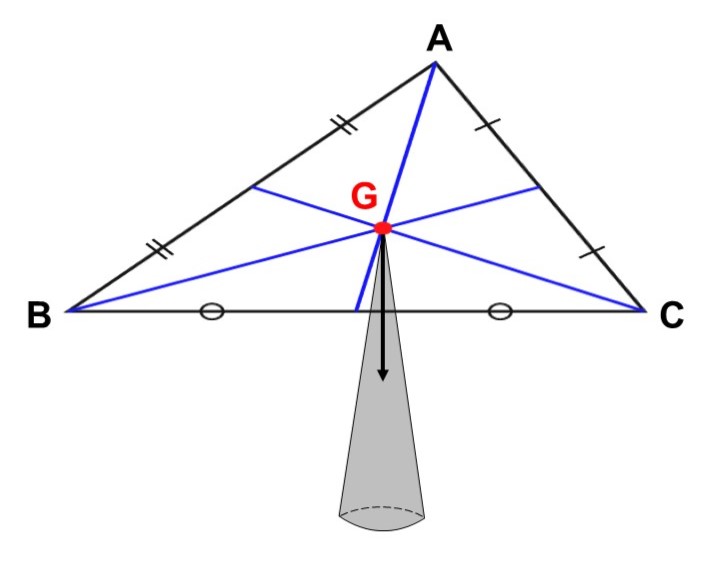
(3)で五角形$\mathrm{ABCDE}$の重心は求まりましたが、はたして本当に$\mathrm{G}$は重心なのでしょうか?
ということで、実際にこの五角形(の模型)を作り、$\mathrm{G}$の位置(赤い点)をボールペンの先で支えてみました↓

確かに倒れずに安定していますね。
物体の重心を知ることは、物を持ち上げたり支えたりといった、日常のよくある場面でも役立ちます。ぜひ普段から意識してみましょう!
参考資料
[1] チャート式 基礎からの数学Ⅰ+A 新課程 (チャート研究所 / 数研出版 2022)