23F　「場合の数にベン図を活用しよう」 ― 集合

こんにちは、まてがめです。

これまで樹形図・順列・組合せといった、場合の数をうまく数えるための方法を学んできました。

• 20F　「場合の数を知る方法」 ― 樹形図
• 21F　「シンプルかつ便利な考え方」 ― 順列
• 22F　「順列の応用」 ― 組合せ

今回は4つ目の方法として集合（しゅうごう）の考え方を学んでいきます。集合というのは簡単に言えば「ある共通点を持つグループ」のことです。集合の考え方が使えるようになると、より複雑な状況に対しても場合の数を計算できるようになります。

集合を考えるための道具 ― ベン図

まずは簡単な例を使って集合の考え方を学んでみましょう。

(1) 数字が8以上

トランプでは1つの数字につき4枚（スペード、ハート、クラブ、ダイヤ）のカードがありますから、数字が8以上（8～13）であるカードの枚数は

$6 \times 4 = 24$

すなわち、24枚となります。

では、これを集合（グループ）として図にしてみましょう。それぞれの集合を簡単に表すために、トランプ全体の集合を$U$（全体集合のことを英語ではUniversal setと言います）、数字が8以上であるカードの集合を$A$で表すことにします。集合を図にする時はベン図と呼ばれる次のような図を描きます。

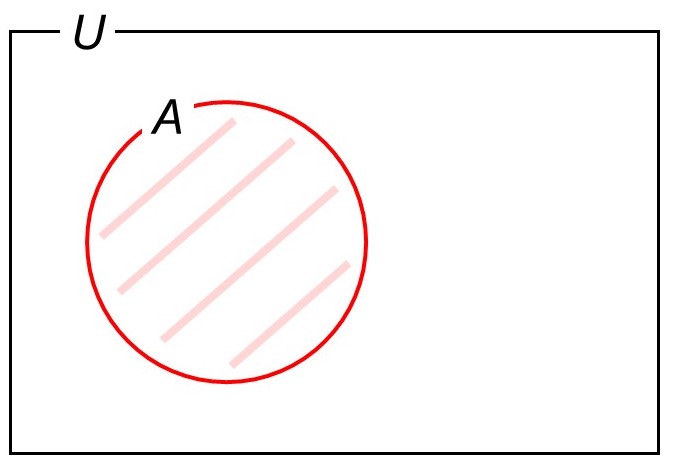
全体集合$U$（トランプ全体）の中に集合$A$（8以上）が含まれているというのがよくわかりますね。

また、それぞれの集合に含まれる要素の数は、数の英語numberの頭文字nを使ってn(○)のように表します。例えば、集合$A$の要素の数は

$n(A) = 24$

と表します。

(2) 数字が7以下

まずは、(1)と同じように考えてみましょう。数字が1～7のカードが4枚ずつあるので、

$7 \times 4 = 28$

よって、この場合は28枚です。

一方、この枚数は集合を用いて求めることもできます。「数字が7以下」というのは、(1)の「数字が8以上」とは逆の場合です。つまりこの集合は、集合A以外の要素から成る集合だと言えます。

このような集合を「$A$の補集合（ほしゅうごう）」といい、$A^c$で表します（cは補集合の英語complementの頭文字）。

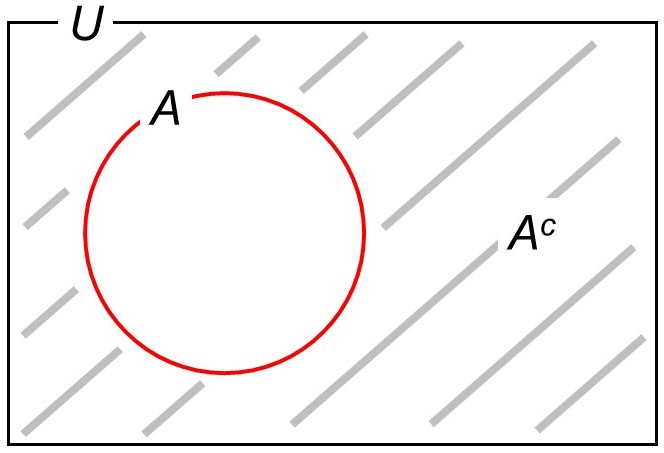
したがって、要素の数（枚数）は次のように計算できます。

$\begin{align}
n(A^c) & = n(U)-n(A) \\[1.5ex]
& = 52-24 \\[1.5ex]
& = 28
\end{align}$

(3) 絵札

絵札は11（ジャック）、12（クイーン）、13（キング）の3種類に対し、それぞれが4枚ずつあるので、

$3 \times 4 = 12$

よって、12枚です。

この集合を$B$とすると、集合$B$（11以上）は集合$A$（8以上）よりも小さいですから、ベン図に描き加えると次のようになります。

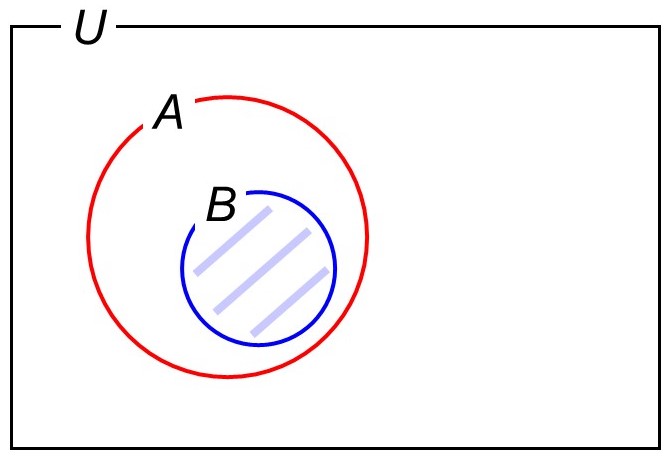
このような時、「$B$は$A$の部分集合（ぶぶんしゅうごう）である」といい、$B \subset A$と表します。「開いている側を集合の大きい方に向ける」と覚えましょう。

(4) マークがハート

マークにはスペード、ハート、クラブ、ダイヤの4種類があり、それぞれ同じ枚数だけありますから、

$52 \div 4 = 13$

よって、13枚です。

この集合を$C$としてベン図に描きこんでみると次のようになります。当然ですが、集合$A$（8以上）とも重なる部分がありますね。

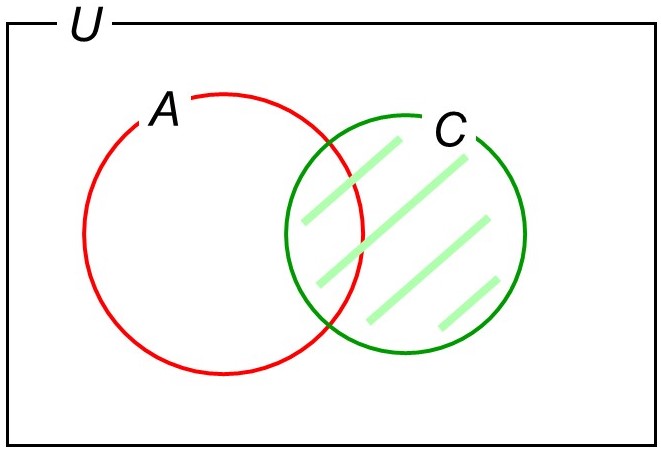
(5) 数字が8以上かつマークがハート

「かつ」と言っているので、どちらの条件も満たす必要があります。今回はハートという1つのマークについて、8以上（8～13）となるカードの枚数を考えればよいので、6枚が答えです。

ベン図では、集合$A$（8以上）と集合$C$（ハート）の共通部分を考えていることになります。共通部分の集合は$A \cap C$と表します。$\cap$を囲いに見立てて「共通部分に囲いをする」と覚えましょう。

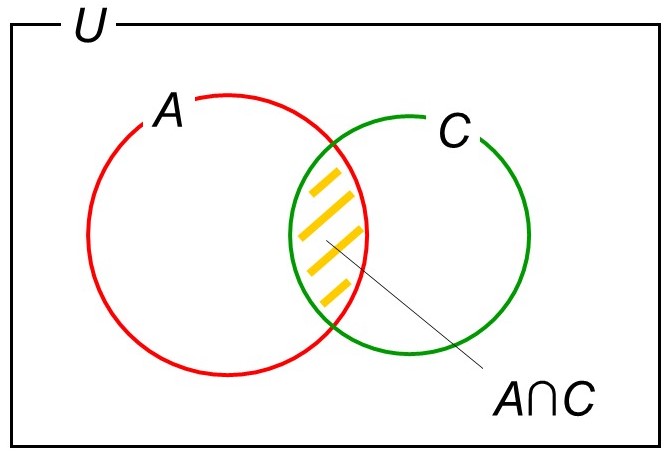
(6) 数字が8以上かつマークがハートではない

「数字が8以上」かつ「マークはハートではない」ということは、「数字が8以上」かつ「マークはスペード・クラブ・ダイヤのいずれか」ということになるので、

$6 \times 3 = 18$

よって、18枚です。

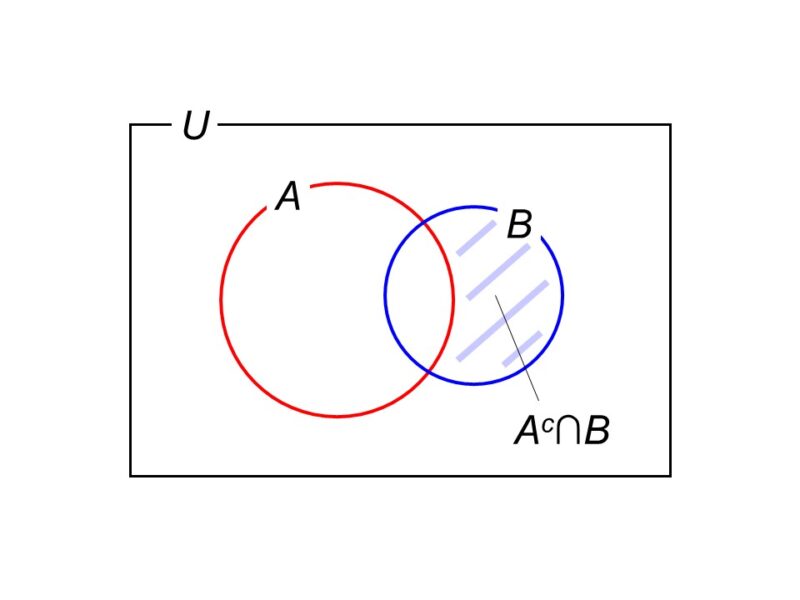
こちらも集合で考えてみましょう。今回考えているのは、集合$A$（8以上）と補集合$C^c$（ハートではない）の共通部分（$A \cap C^c$）ですから、ベン図では次に示す部分になります。

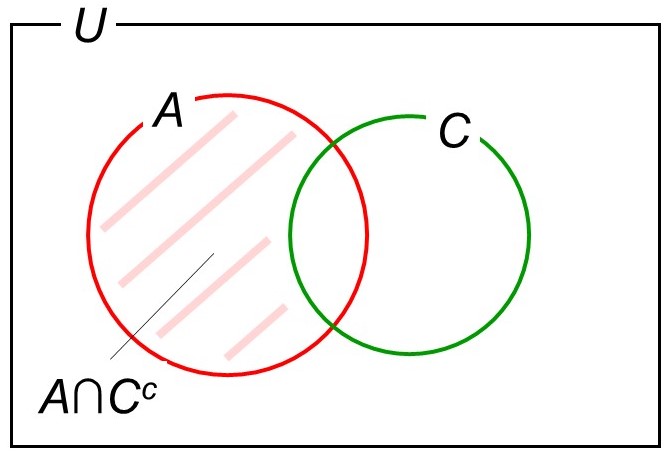
これは集合$A$から共通部分$A \cap C$を取り除いたものとみなせるので、次のような計算で答えがわかりますね。

$\begin{align}
n(A \cap C^c) & = n(A)-n(A \cap C) \\[1.5ex]
& = 24-6 \\[1.5ex]
& = 18
\end{align}$

(7) 数字が8以上またはマークがハート

「または」と言っているので、どちらか一方の条件さえ満たせばよいことになります。ベン図で見ると、$A$（8以上）と$C$（ハート）を合わせたような集合です。このような集合を「$A$と$C$の和集合（わしゅうごう）」といい、$A \cup C$で表します。$\cup$を2本の腕に見立てて「両腕で2つの集合を持つ」と覚えましょう。

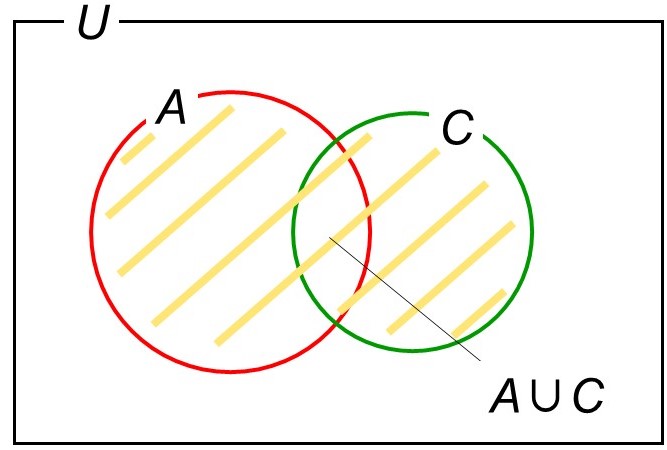
和集合と言うくらいですから、要素の数についても「$n(A)$と$n(C)$を足せばよいのでは？」と考えてしまいがちですが、実はこれではうまくいきません。というのも、この計算では共通部分の要素の数$n(A \cap C)$において重複が生じてしまうからです。

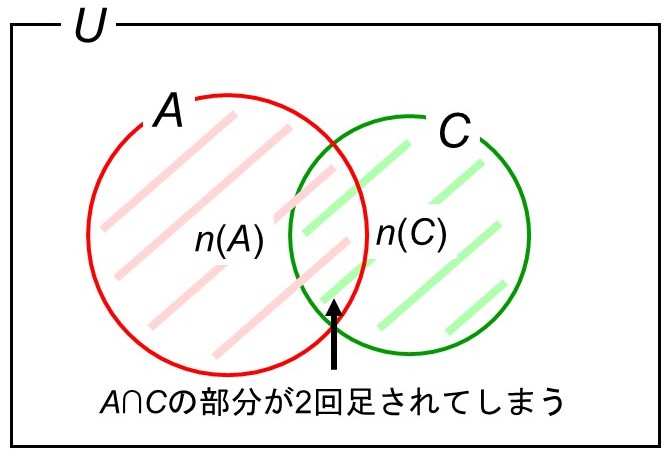
なので、重複分を差し引きましょう。すなわち、次の計算であれば答えが求まります。

$\begin{align}
n(A \cup C) & = n(A)+n(C)-n(A \cap C) \\[1.5ex]
& = 24+13-6 \\[1.5ex]
& = 31
\end{align}$

よって、31枚です。

ここで一度、集合で使う記号についてまとめておきましょう。

集合（ベン図）を使って場合の数を数えよう

では、実際に集合（ベン図）を使って、複雑な条件を満たす場合の数を数えてみましょう。次の例題を見てください。

今、碁盤の目のように設計されていることで有名な都市へ観光に来ている。現在地Sから目的地Gへは最短経路で行きたいが、時間があれば途中でお店A, Bにも立ち寄りたいと考えている。

次の条件を満たす経路は何通りあるか？

(1) 目的地Gまでのすべての経路

(2) お店Aに立ち寄ってから目的地Gに行く経路

(3) お店Bに立ち寄ってから目的地Gに行く経路

(4) お店Aまたはお店Bに立ち寄ってから目的地Gに行く経路

(5) お店Aには立ち寄らず、お店Bに立ち寄ってから目的地Gに行く経路

(6) お店Aまたはお店Bに立ち寄らず目的地Gに行く経路

(1) 目的地Gまでのすべての経路

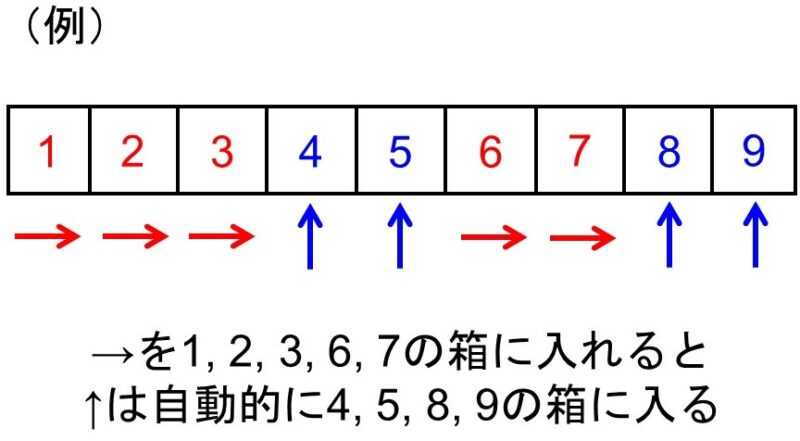
地図を見てわかるように、SからGへ最短で行くためには必ず東へ5マス、北へ4マス進む必要があります。そこで、東へ1マス進むことを→、北へ1マス進むことを↑で表すことにすると、5個の→と4個の↑の並べ方を1つの経路に対応させることができます。

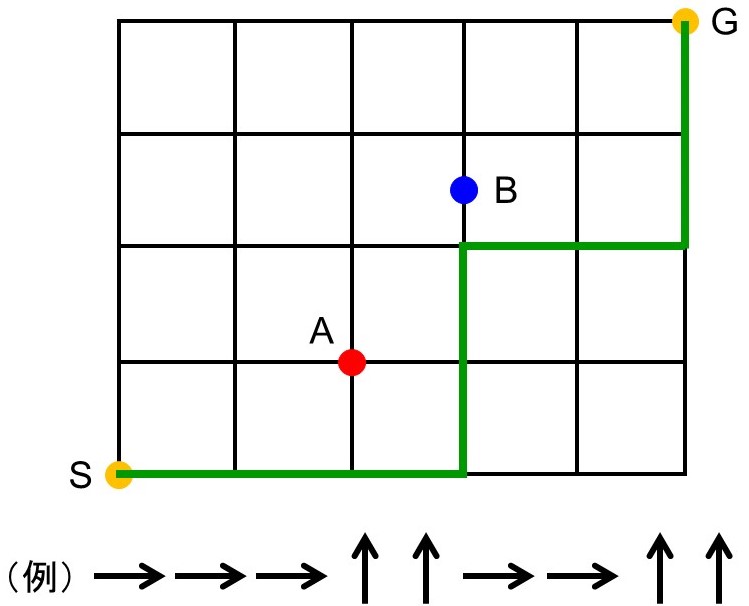
したがって、5個の→と4個の↑（計9個の矢印）の順列について場合の数を数えれば経路の数がわかります。ただし、5個の→と4個の↑にはそれぞれ区別がないので、これらの並べ方には重複があることに注意してください（区別がつかないものの順列については21Fで解説しています）。

$\dfrac{9!}{5! \times 4!} = 126$

よって、答えは126通りです。これを全体集合$U$としておきましょう。

今回の経路の数は、次のように考えると組合せとしても計算できます。

計9個の矢印の並べ方というのは、1～9の番号が書かれた9個の箱に矢印を入れる場合の数として対応させることができます。例えば、どの番号の箱に5個の→を入れるかを決めれば、残り4個の箱に自動で↑が入ることになるので、並べ方もただ一つに決まるわけです。

このように考えれば、「9個の箱から→を入れるための5個を選ぶ方法」として場合の数を数えればよいので、

${}_9 \mathrm{C}_5 = \dfrac{9 \times 8 \times 7 \times 6 \times 5}{5 \times 4 \times 3 \times 2 \times 1} = 126$

と計算できます。

(2) お店Aに立ち寄ってから目的地Gに行く経路

まず、SからAまでの最短経路を考えます。地図によれば、SからAに行くには東へ2マス、北へ1マス進む必要があります。よって、2個の→と1個の↑（計3個の矢印）の順列について場合の数を数えればよいので、こちらの場合の数は次のように計算できます。

$\dfrac{3!}{2!} = 3$

続いてAからGまでの最短経路を考えます。地図によれば、AからGに行くには東へ3マス、北へ3マス進む必要があります。よって、3個の→と3個の↑（計6個の矢印）の順列について場合の数を数えればよいので、こちらの場合の数は次のように計算できます。

$\dfrac{6!}{3! \times 3!} = 20$

以上から、求める場合の数は

$3 \times 20 = 60$

つまり、60通りとなります。この集合を$A$としておきましょう。

(3) お店Bに立ち寄ってから目的地Gに行く経路

Aは交差点にありましたが、Bは道の途中にありますね。この道の端点をP₁, P₂とすると、Bに立ち寄るためには必ずP₁P₂を必ず通らなくてはならないということになります。

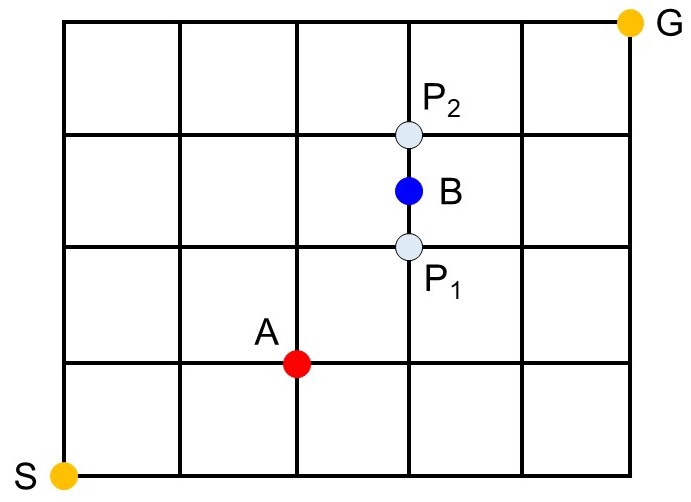
そこでまず、SからP₁までの最短経路を数えてみましょう。地図によれば、SからP₁に行くには東へ3マス、北へ2マス進む必要があります。よって、3個の→と2個の↑（計5個の矢印）の順列について場合の数を数えればよいので、こちらの場合の数は次のように計算できます。

$\dfrac{5!}{3! \times 2!} = 10$

続いて、P₂からGまでの最短経路を数えてみましょう。地図によれば、P₂からGに行くには東へ2マス、北へ1マス進む必要があります。よって、2個の→と1個の↑（計3個の矢印）の順列について場合の数を数えればよいので、こちらの場合の数は次のように計算できます。

$\dfrac{3!}{2!} = 3$

以上から、求める場合の数は

$10 \times 3 = 30$

つまり、30通りとなります。この集合を$B$としておきましょう。

(4) お店Aまたはお店Bに立ち寄ってから目的地Gに行く経路

「Aに立ち寄る」または「Bに立ち寄る」場合なので、和集合$A \cup {B}$に対応します。ベン図では次に示す部分です。

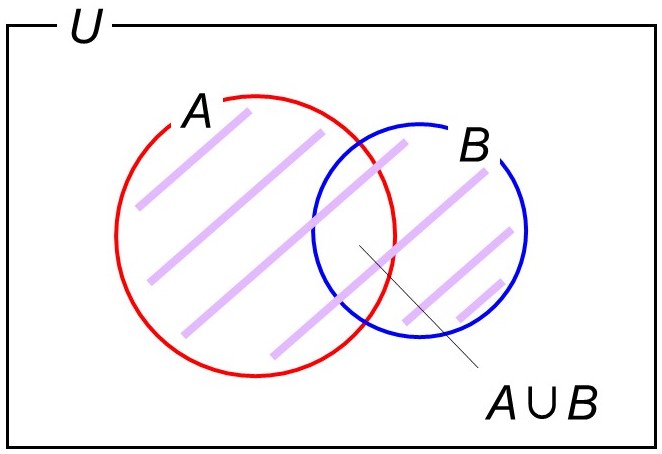
復習ですが、和集合における要素の数は次の式で計算できます。重複分を差し引くのがポイントでしたね。

$n(A \cup B) = n(A)+n(B)-n(A \cap B)$

(2)で$n(A)=60$、(3)で$n(B)=30$はすでに求めていますから、まだ計算していない$A\cap{B}$の要素の数$n(A\cap{B})$を求めておきましょう。これは「AとBの両方に立ち寄ってからGに行く経路の数」ですね。

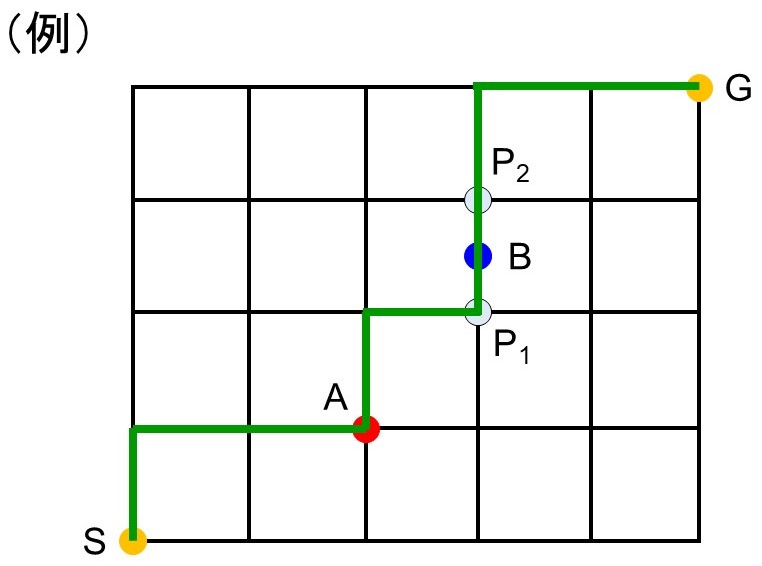
SからAまでの最短経路の本数は、2個の→と1個の↑の順列を考えて、

$\dfrac{3!}{2!} = 3$

AからP₁までの最短経路の本数は、1個の→と1個の↑の順列を考えて、

$2! = 2$

P₂からGまでの最短経路の本数は、2個の→と1個の↑の順列を考えて、

$\dfrac{3!}{2!} = 3$

よって、AとBの両方に立ち寄ってからGに行く経路の数$n(A \cap B)$は

$n(A \cap B) = 3 \times 2 \times 3 = 18$

以上から、求める経路の数は

$\begin{align}
n(A \cup B) & = n(A)+n(B)-n(A \cap B) \\[1.5ex]
& = 60+30-18 \\[1.5ex]
& = 72
\end{align}$

つまり、72通りとなります。

(5) お店Aには立ち寄らず、お店Bに立ち寄ってから目的地Gに行く経路

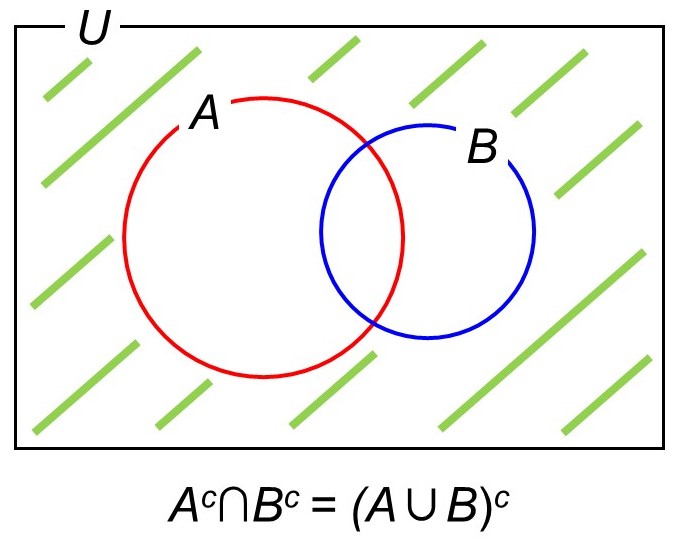
「Aに立ち寄らない」かつ「Bに立ち寄る」場合なので、共通部分$A^c \cap B$に対応します。ベン図では次に示す部分です。

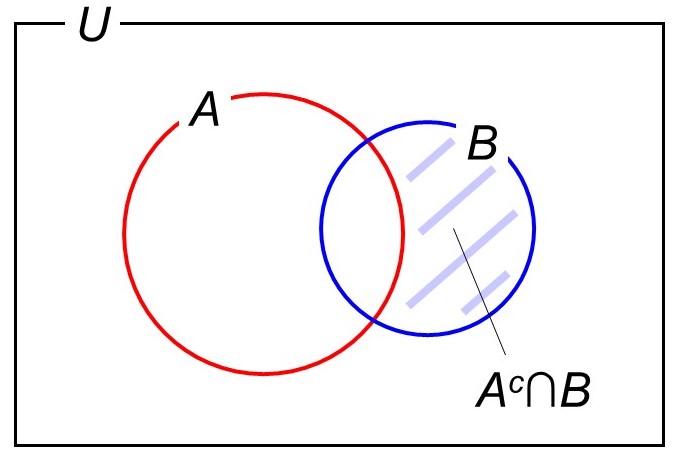
これは集合$B$から共通部分$A \cap B$を除いた部分なので、経路（要素）の数は次のように計算すればよいですね。

$\begin{align}
n(A^c \cap B) & = n(B)-n(A \cap B) \\[1.5ex]
& = 30-18 \\[1.5ex]
& = 12
\end{align}$

つまり、12通りです。

(6) お店Aまたはお店Bに立ち寄らず目的地Gに行く経路

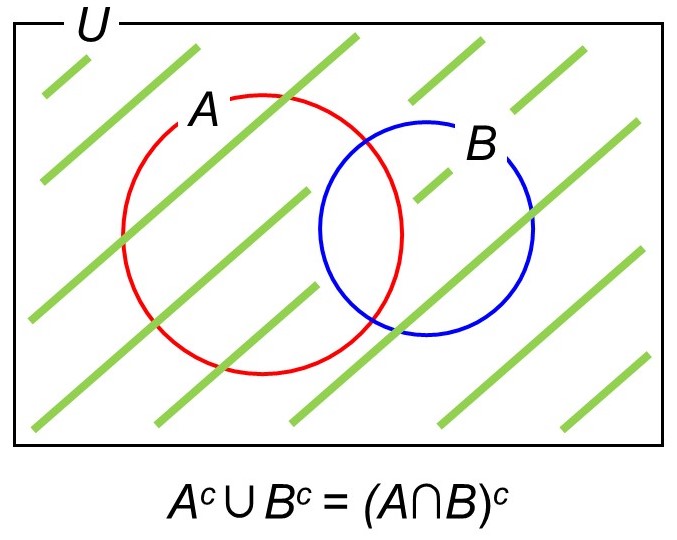
「Aに立ち寄らない」または「Bに立ち寄らない」場合なので、和集合$A^c \cup B^c$に対応します。ベン図では次に示す部分です。

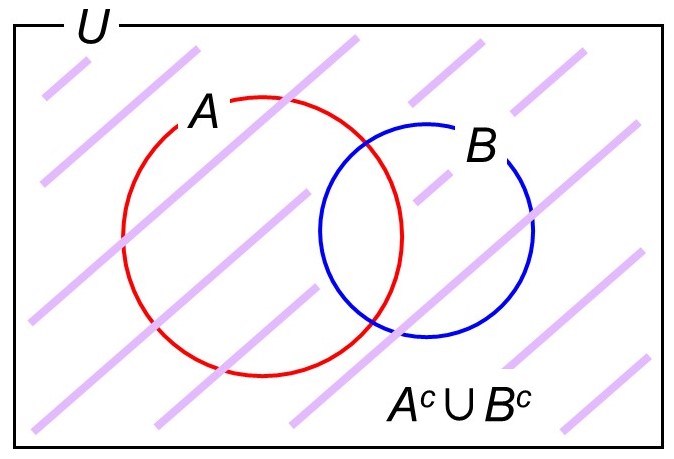
ベン図にしてみると、$A$と$B$の共通部分の補集合$(A \cap B)^c$と見ることもできますね。

$A^c \cup B^c = (A \cap B)^c$

したがって、「経路全体の数$n(U)$」から「AとBの両方に立ち寄る場合の経路の数$n(A \cap B)$」を引けば答えがわかります。

$\begin{align}
n(A^c \cup B^c) & = n((A \cap B)^c) \\[1.5ex]
& = n(U)-n(A \cap B) \\[1.5ex]
& = 126-18 \\[1.5ex]
& = 108
\end{align}$

つまり、108通りとなります。

全体集合$U$の中に集合$A$と集合$B$があり、共通部分$A\cap{B}$が存在するとします。この時、次の2つの式が成り立ちます。

[1] $A^c \cup B^c = (A \cap B)^c$

[2] $A^c \cap B^c = (A \cup B)^c$

これらはド・モルガンの法則と呼ばれています。補集合を「それぞれの集合」に対して考える場合と「共通部分もしくは和集合」に対して考える場合で、共通部分の記号$\cap$と和集合の記号$\cup$が入れかわるのが面白いですね。

まとめ

今回は集合の考え方について学びました。最も大切なポイントは「共通点を持つグループ（集合）を考え、その関係を図に表す（ベン図にする）」ということです。

ベン図においては集合同士の関係が一目でわかるので、条件が複雑な場合の数も計算することができるようになります。必要に応じて活用していきましょう！

今回はここまでです。お疲れさまでした！