今回の問題はこちらです。(※33Fまでの内容を理解していることが前提です!)
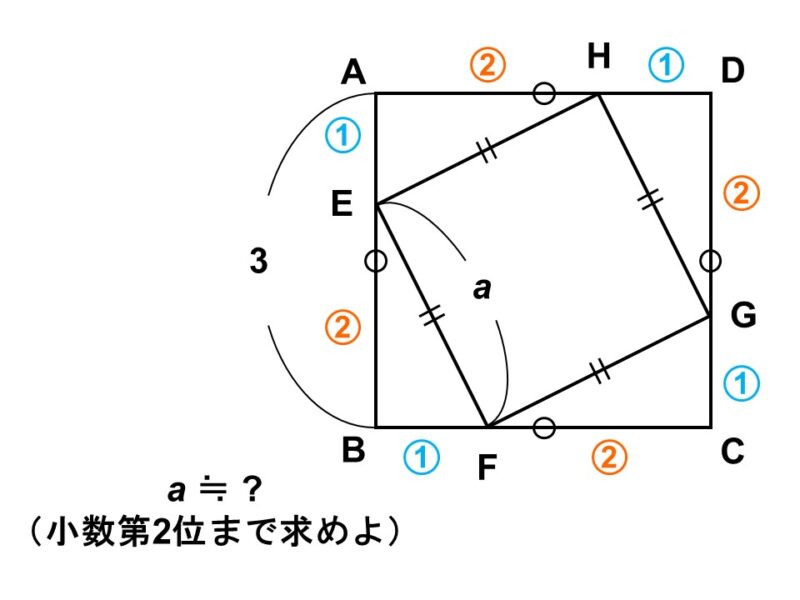
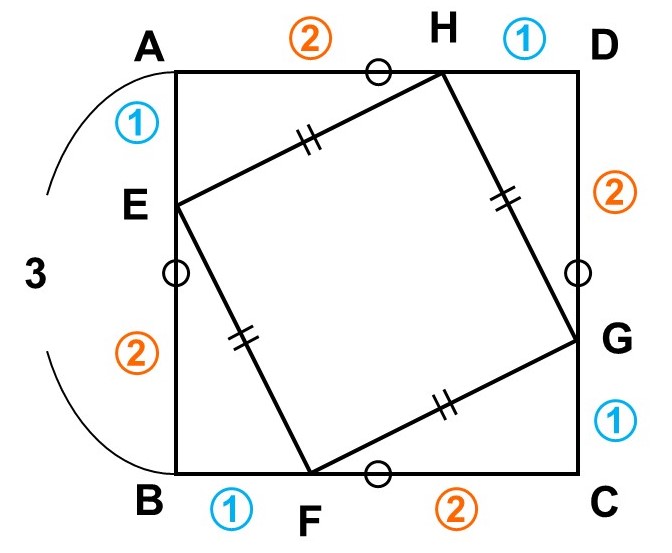
1辺の長さが3の正方形$\mathrm{ABCD}$がある。この正方形に対して、各辺を1 : 2に内分する点$\mathrm{E}$, $\mathrm{F}$, $\mathrm{G}$, $\mathrm{H}$を打って結ぶことで、新しい正方形$\mathrm{EFGH}$を作った。
(1) 正方形$\mathrm{EFGH}$の面積を求めなさい。
(2) 正方形$\mathrm{EFGH}$の1辺の長さを、小数点第3位を「四捨五入」して小数点第2位まで求めなさい。
ここで「四捨五入」とは、注目している位が4以下の数なら切りすて、5以上の数なら上の位の数を1くり上げることを表す。
(例)
1.414 →1.41(小数点第3位が4以下なので切りすて)
1.618 → 1.62(小数点第3位が5以上なので小数点第2位を1くり上げ)
(1) 正方形の1辺はわからない。ならどうする?
(1)では正方形$\mathrm{EFGH}$の面積を求めます。正方形の面積は底辺×高さ(1辺×1辺)で計算できますから、辺の長さから面積は計算できます。しかし今回、それはあたえられていません。
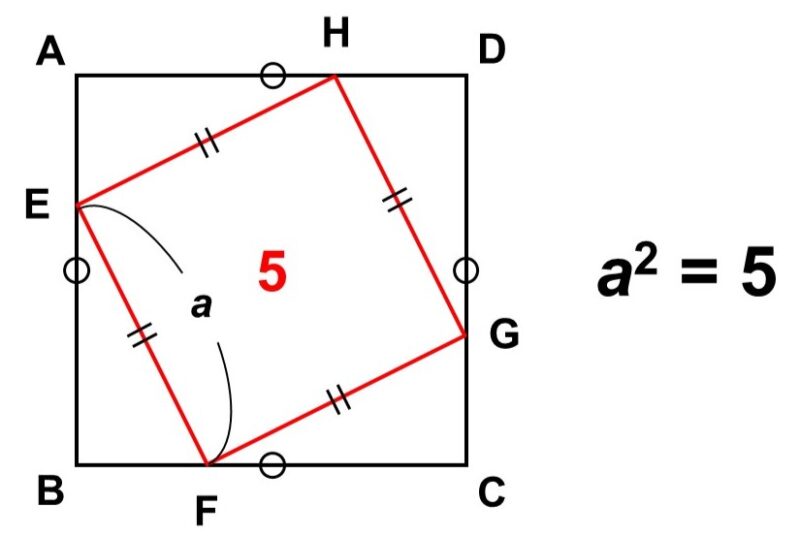
したがって、別の方法で考える必要があります。そこで、図をよく見てみると、正方形$\mathrm{EFGH}$は合同な4つの直角三角形($\triangle \mathrm{AEH}$, $\triangle \mathrm{BFE}$, $\triangle \mathrm{CGF}$, $\triangle \mathrm{DHG}$)に囲まれているのがわかります。
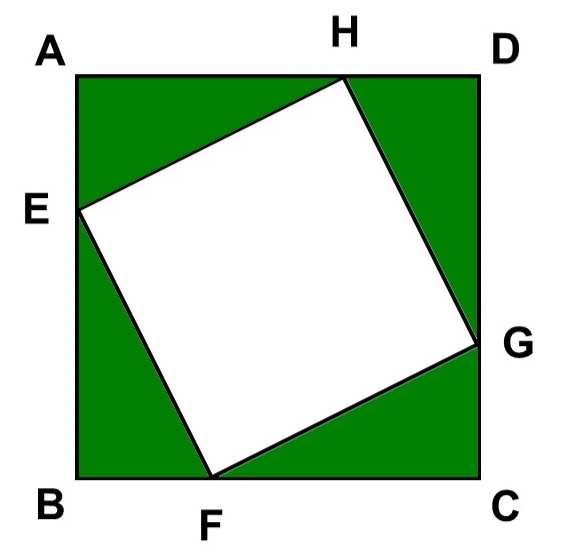
全体は1辺の長さが3とわかっている正方形$\mathrm{ABCD}$ですから、ここから4つの直角三角形を切り取るようにして計算すれば、正方形$\mathrm{EFGH}$の面積がわかりそうです。
まず正方形$\mathrm{ABCD}$の面積は、
$3 \times 3 = 9$
です。
次に直角三角形の方ですが、例えば$\triangle \mathrm{CGF}$に注目してみます。$\mathrm{E}$, $\mathrm{F}$, $\mathrm{G}$, $\mathrm{H}$は長さ3の各辺を1 : 2に内分しているので、底辺は2、高さは1とわかりますね。
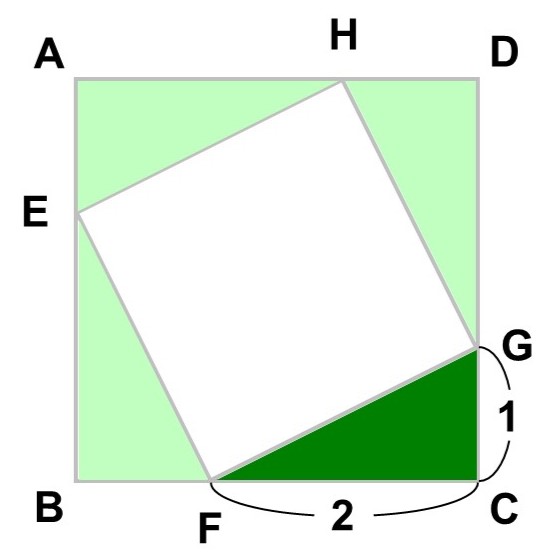
三角形の面積は底辺×高さ÷2で計算できるので、この直角三角形の面積は
$\dfrac{1 \times 2}{2} = 1$
となります。
あとは、この面積4つ分を正方形$\mathrm{ABCD}$から切り取ればよいので、求める面積は
$9-4 \times 1 = 5$
となります。
(2) わからない長さをどう見積もるか?
(1)で1辺の長さがわからない正方形$\mathrm{EFGH}$の面積を求めることができました。では、そもそもこの正方形の1辺の長さは一体いくらなのでしょうか?
正方形の面積は底辺×高さ(1辺×1辺)で計算できるので、正方形$\mathrm{EFGH}$の1辺の長さを例えば$a$で表すことにすると、
$a \times a = a^2 = 5$ …<*>
を満たすような$a$、すなわち「2乗して5になる数」を考えればよいわけです(累乗については24Fで解説しています)。
試しに自然数(1, 2, 3, …)で考えてみると、
$\begin{align}
1^2 &= 1 \\[1.5ex]
2^2 &= 4 \\[1.5ex]
3^2 &= 9
\end{align}$
となるので、自然数の中に<*>を満たすような数はありません。
そこで、もう少しくわしく調べてみることにします。2乗した後の数を比べてみると、不等号(19Fで解説しています)を使って
$2^2 = 4 < 5 < 9 =3^2$
と書けるので、今の実験から少なくとも次のことは言えます。
$2 < a < 3$
つまり、$a$は「2よりも大きく、3よりも小さい」ということです。
そこで今度は、2と3の間にある数について調べてみます。試しに真ん中の2.5を2乗してみると、
$2.5^2 = 6.25$
となって5よりも大きいので、$a$は2.5よりも小さい数だとわかります。これを踏まえて、2.5から0.1ずつ小さい数(2.4, 2.3, …)で2乗を計算してみると、
$\begin{align}
2.4^2 &= 5.76 \\[1.5ex]
2.3^2 &= 5.29 \\[1.5ex]
2.2^2 &= 4.84
\end{align}$
となります。よって、
$2.2^2 = 4.84 < 5 < 5.29 = 2.3^2$
ですから、次のことが言えます。
$2.2 < a <2.3$
さらに実験してみます。2.2と2.3の真ん中である2.25を2乗してみると、
$2.25^2 = 5.0625$
わずかに5より大きかったですね。したがって、$a$は2.25よりも小さい数ということになるので、先ほどと同じく0.01ずつ小さい数(2.24, 2.23, …)で2乗を計算してみます。
$\begin{align}
2.24^2 = 5.0176 \\[1.5ex]
2.23^2 = 4.9729
\end{align}$
よって、
$2.23^2 = 4.9729 < 5 < 5.0176 = 2.24^2$
なので、次のことが言えます。
$2.23 < a <2.24$
ここまでの実験から
$a = 2.23 \hspace{2pt} \text{…}$
と表せることがわかりました。さらに同じことをくり返して下の位を調べてもよいですが、今回は小数点第3位を四捨五入して小数第2位まで求めればよいので、2.234, 2.235の2乗を計算してみて、「切りすて」か「くり上げ」を決めればOKです。
$\begin{align}
2.234^2 &= 4.990756 < 5\\[1.5ex]
2.235^2 &= 4.995225 < 5
\end{align}$
したがって$2.235 < a$であり、小数第3位は5以上の数なので、求める長さの近似値は小数第2位をくり上げて2.24となります。
$a \fallingdotseq 2.24$
知りたい値が正確にわからない場合、このように小さい数と大きい数ではさむことで近似値を見積もることができます。
この方法は、34Fで登場する「円周率」の値を近似する時にも使われます。
確かに存在するが表しきれない数 ― 無理数
(2)では、およその値(近似値)として正方形$\mathrm{EFGH}$の1辺の長さを求めました。ちなみに$a$の値をさらに調べていくと、実はまったく終わりが見えないことがわかります。
$a = 2.2360679 \hspace{2pt} \text{…}$
加えてこの数は、通常の分数を使っても表すことができません。このような数は無理数(むりすう)と呼ばれています。
一方で正方形$\mathrm{EFGH}$は実際に描くことができますから、このような無理数は確かに存在しています。ただ、無理数が出てくるたびに毎回近似値を求めるのはめんどうな上、より正確な値で扱おうにも、小数点以下の桁数が増えてしまうので、計算では使いにくいです。
こんな時に活躍するのが平方根(へいほうこん)と呼ばれるものです。
0以上のある数$x$を2乗すると$y$という数になる($x^2 = y$)場合、$x$は「$y$の平方根である」といい、ルート(根号)という記号√を使って次のように表します。
$x = \sqrt{y}$
今回の場合、$a$を2乗すると5になるので、$a$は5の平方根として次のように表せます。
$a = \sqrt{5}$
ルートを使うメリットの1つが、まず表記がシンプルになるということ。そしてもう1つが、この定義に合わせた計算のルールさえ決めておけば、常に無理数を正確な値で扱えるということです。
例えば、T6で紹介した黄金比$\phi$は、ルートを使うと正確な値として次のようにシンプルに表せます。
$\phi = \dfrac{1+\sqrt{5}}{2}$
平方根の扱い方については、また別の機会でお話しします。