こんにちは、まてがめです。
前回は、平面図形における重要な概念として「角度（垂直・平行）」について学びました。角度、そして垂直・平行は、あらゆる図形を特徴づけるための要素となる考え方です。
ここまでの階で、平面図形を学んでいくのに最低限必要な考え方はそろったので、いよいよ今回から平面図形の基礎である三角形（さんかっけい）について学んでいきます。
最もシンプルな「閉じた図形」 ― 三角形
今、平面上に「閉じた図形」を描くとします。ここでいう「閉じた図形」とは、内側と外側を分けるような図形のことです。この時、このような図形は何本の線があれば作れるでしょうか？
1本ではただの線しか描けません。また、2本の場合も、角度を変えたり伸び縮みさせて交わらせることはできますが、やはり閉じた図形は描けません。
しかし、3本の線を用意した場合、1本が別の2本と異なる点で交わるように線を引くことで閉じた図形を描くことができます。
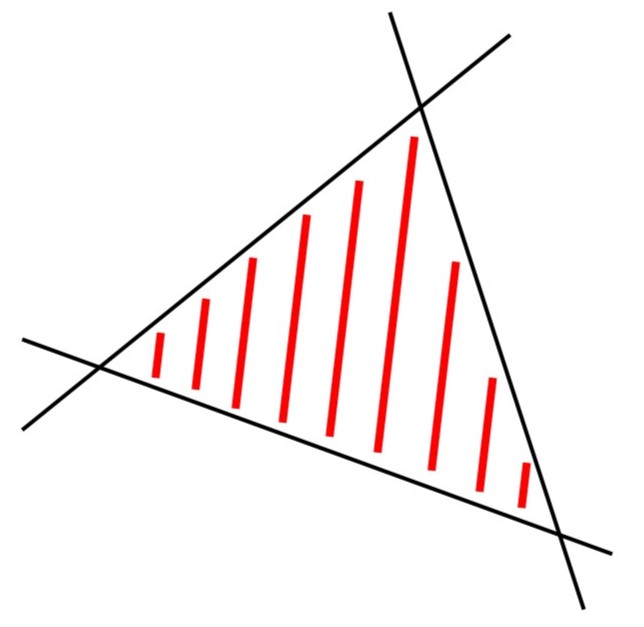
このような図形を三角形（さんかっけい）といいます。ここで、三角形の各部分について説明しておきましょう。
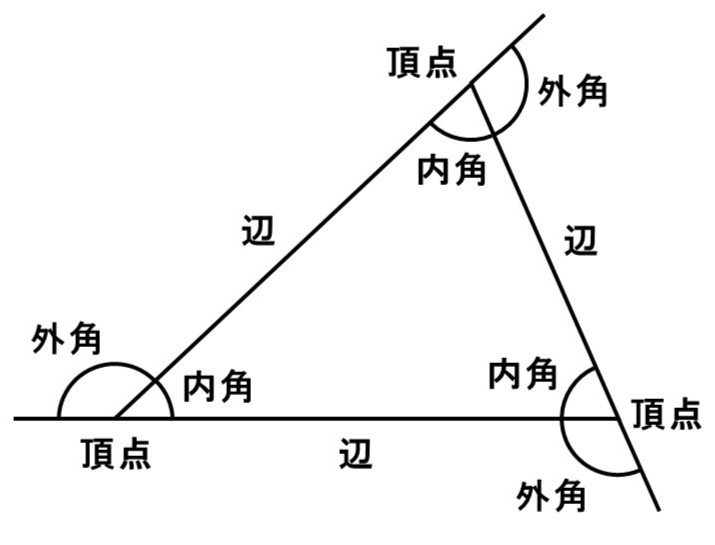
三角形を形作っている線分を辺（へん）といい、2辺の交点を頂点（ちょうてん）といいます。頂点にできる角はそのまま角（かく）といい、内側を内角（ないかく）、外側を外角（がいかく）といいます。
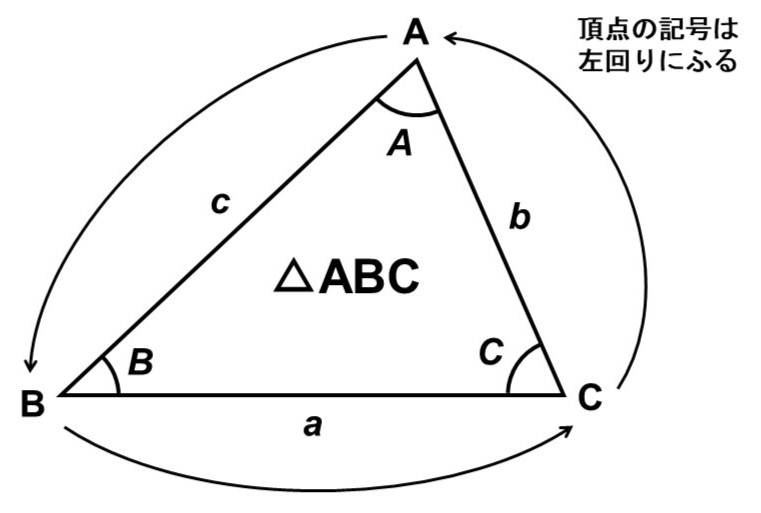
また、各パーツに記号をふる時は、次のように行うのが一般的です。
- 頂点：$\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$
- 内角：$A$, $B$, $C$
- 辺：$a$, $b$, $c$ ← 頂点の向かいにある辺（対辺）のアルファベットに対応
これに応じて、三角形そのものを示す時は△ABCと表します。
3本の線があって初めて閉じた図形である三角形が作れるわけですが、4本なら四角形、5本なら五角形、6本なら六角形…といったように、線が3本以上であれば閉じた図形を作ることができます。これらはまとめて多角形（たかっけい）と呼ばれています。
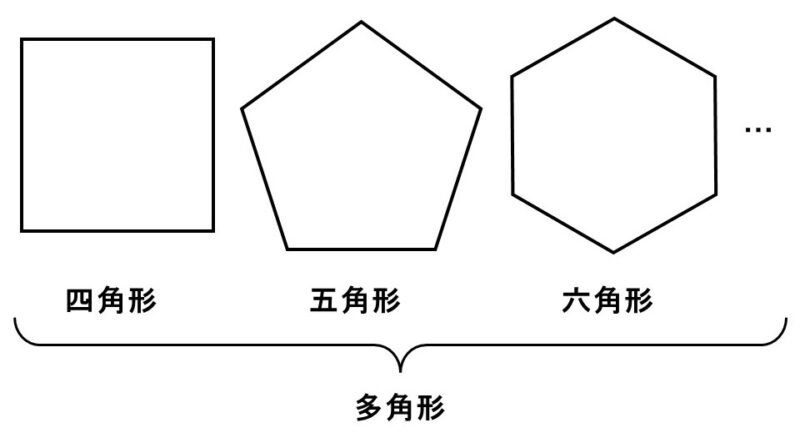
ただ、三角形以外の図形は「三角形の集まり」とみなすこともできます。例えば、四角形、五角形、六角形は、次のように線（対角線）で区切ってみると三角形が組み合わさってできていることがわかります。
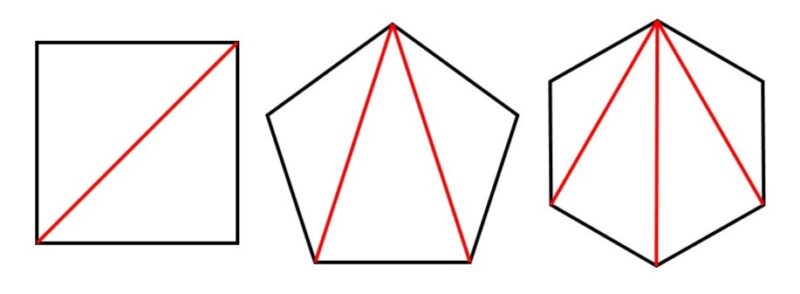
これはつまり、三角形について理解できれば、おのずと他の閉じた図形についても理解できるということを意味しています[1], [2]。
三角形の持つ性質
では、三角形がどのような性質を持っているのか見ていきましょう。
内角の和は180°
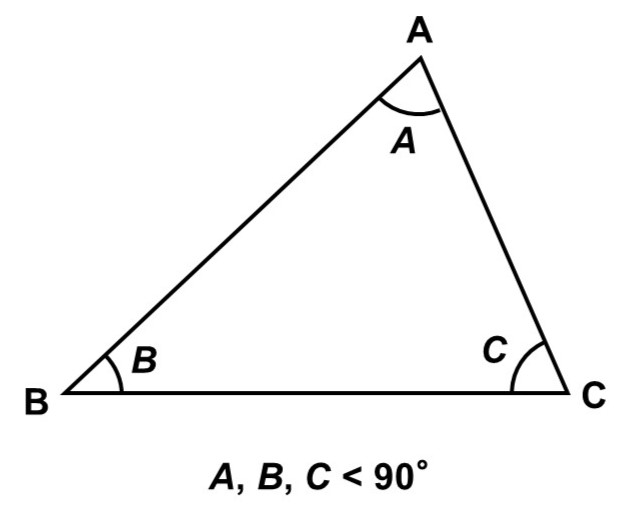
例えば、$\triangle \mathrm{ABC}$において、$A$を変えていった時に何が起こるか考えてみましょう。
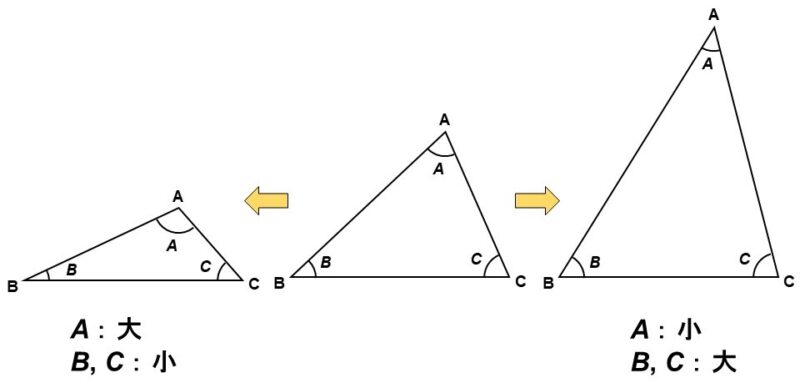
$A$を大きくしていった場合、$B$, $C$は小さくなっていきます。一方で$A$を小さくしていくと、今度は$B$, $C$が大きくなっていきます。
ここから「三角形の内角の和は、いつも同じ角度$\theta_{\mathrm{c}}$になるのではないか？」という予想が立ちます（cは「定数」の英語constantの頭文字）。
$A+B+C = \theta_{\mathrm{c}}$
そしてこの予想は正しく、三角形の内角の和は必ず180°になることが知られています。
$A+B+C = 180^{\circ}$
では、なぜ180°になるのでしょうか？ここで、平面図形においてよく使われる証明（しょうめい）という操作を紹介します。
証明とは、「すでに正しいとわかっている事柄（公理・定理）を使って、新しい法則と思われるもの（命題）が、本当に正しい（真である）ことを示す」操作です。これを使うことで、正しい事柄の上に新たに正しいとわかった事柄を積み上げていくことができます。
「三角形の内角の和が180°になる」ことは、これまでに学んだ「平行」や「錯角」を使って次のように証明することができます。
命題：
「三角形の内角の和は180°になる」
証明：
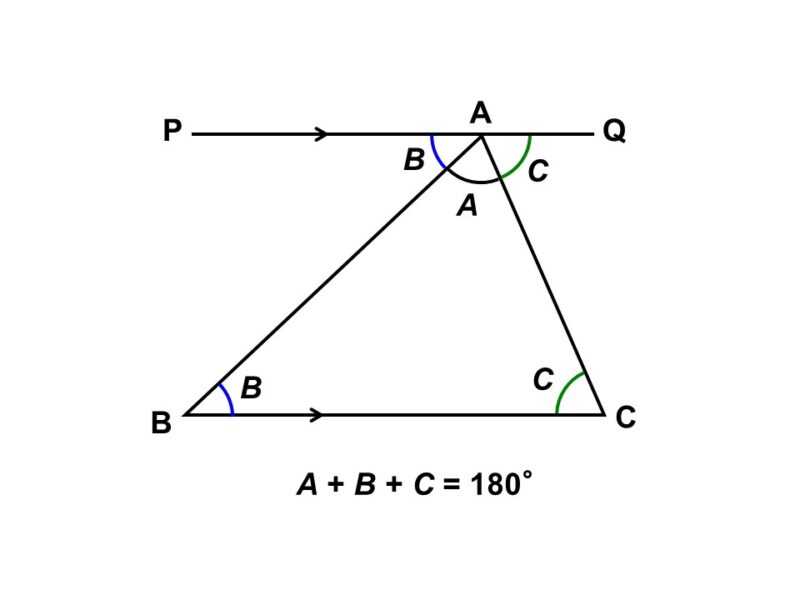
任意の$\triangle \mathrm{ABC}$を用意し、頂点$\mathrm{A}$を通って辺$\mathrm{BC}$に平行な線分$\mathrm{PQ}$を引く。
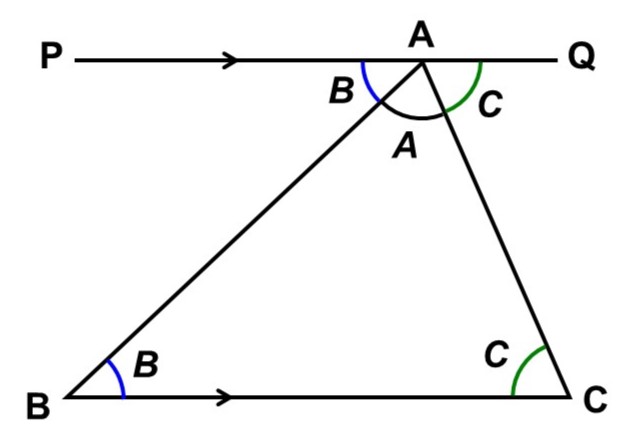
この時、線分$\mathrm{PQ}$に注目すると、
$\angle \mathrm{PAB}+A+\angle \mathrm{CAQ} = 180^{\circ} \hspace{5pt} <1>$
$\mathrm{PQ} /\!/ \mathrm{BC}$より、錯角が等しいので、
$\angle \mathrm{PAB} = B$, $\angle \mathrm{CAQ} = C \hspace{5pt} <2>$
よって<2>を利用すると、<1>は次のように変形できる。
$B+A+C = 180^{\circ}$
したがって、命題が真である。（証明終）
これは三角形における重要な性質で、いろんな場面で活躍します。「内角と外角の関係」が良い例でしょう。
今、$\triangle \mathrm{ABC}$の頂点$\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$における外角を$A’$, $B’$, $C’$とします。
ここで頂点$\mathrm{A}$に注目すると、直線上の角度は180°となるので、
$A+A’ = 180^{\circ}$
が成り立ちます。一方、先ほど証明したように内角の和は180°なので、
$A+B+C = 180^{\circ}$
も成り立ちます。つまり「$A’$あるいは$B+C$に対して$A$を足すと、どちらも180°になる」ということですから、$A’$と$B+C$は等しいということがわかります。
$A’ = B+C$
同じようにして次も成り立ちます。
$B’ = C+A$, $C’ = A+B$
このように「三角形の内角の和が180°になる」ことから、もう一つの性質「外角は隣り合わない内角の和に等しい」ということもわかるわけです。
三角形は内角の大きさに応じて次の3種類に分類されます。
※不等号（<, >）については19Fの小見出し「通分」の箇所で解説しています。
- 鋭角三角形
90°（直角）よりも小さい角のことを鋭角（えいかく）といい、3つの角すべてが鋭角である三角形を鋭角三角形といいます。
- 直角三角形
3つの角のうちの1つが90°（直角）である三角形を直角三角形といいます。なお、三角形の内角の和は180°なので、直角三角形では直角以外の内角の和がちょうど90°となります。
- 鈍角三角形
90°（直角）よりも大きい角を鈍角（どんかく）といい、3つの角のうちの1つが鈍角である三角形を鈍角三角形といいます。
また、特別な形の三角形にもそれぞれ名前がついています。
- 二等辺三角形
二等辺三角形は「2辺の長さが等しい三角形」です。等しい2辺がなす角を頂角、それ以外の角を底角といい、底角が等しいという性質があります（これについては次回証明します）。
- 直角二等辺三角形
直角二等辺三角形は「頂角が90°（直角）である二等辺三角形」です。底角が等しく、その和が90°になることから、底角は45°になります。
- 正三角形
正三角形は「3辺の長さが等しい」三角形です。二等辺三角形の特別な場合であり、内角がすべて等しいため、その角度は$180^{\circ} \div 3 = 60^{\circ}$となります。
辺と角の大小関係
三角形において、「辺」と「角」には密接なつながりがあります。
例えば$\triangle \mathrm{ABC}$において、$b < c$であるとします。この時、辺のそれぞれの向かいにある角（対角）についても同じ大小$B < C$が成り立ちます。
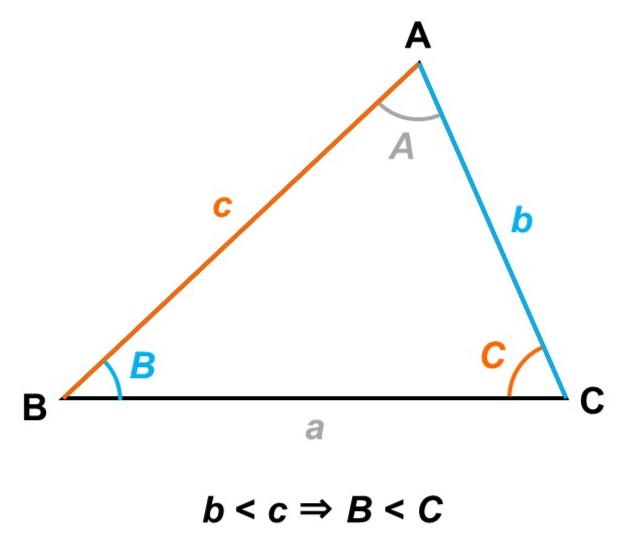
これは感覚的にも理解しやすいですが、二等辺三角形の性質（＝底角が等しい）を利用することで、きちんと証明を行うこともできます[3]。
命題：
「$\triangle \mathrm{ABC}$において、$b < c$ならば$B < C$が成り立つ」
証明：
$b < c$の時、辺$\mathrm{AB}$上には$\mathrm{AD} = \mathrm{AC}$となるような点$\mathrm{D}$をとることができる。
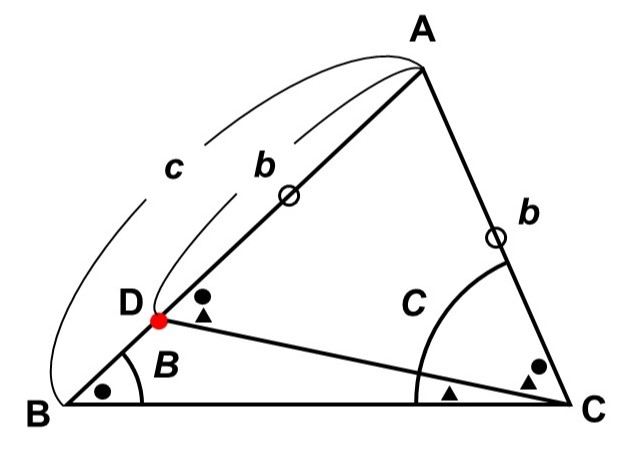
すると、$\triangle \mathrm{ADC}$は$\mathrm{AD} = \mathrm{AC}$の二等辺三角形なので、底角が等しく、
$\angle \mathrm{ADC} = \angle \mathrm{ACD} \hspace{5pt} <1>$
ここで$\triangle \mathrm{DBC}$に注目すると、外角は隣り合わない内角の和に等しいから、
$\begin{align}
\angle \mathrm{ADC} &= \angle \mathrm{DBC}+\angle \mathrm{BCD} \\[1.5ex]
&= B+\angle \mathrm{BCD}
\end{align}$
これより、
$B < \angle \mathrm{ADC} \hspace{5pt} <2>$
また、$C = \angle \mathrm{ACD}+\angle \mathrm{BCD}$なので、
$\angle \mathrm{ACD} < C \hspace{5pt} <3>$
よって<1>, <2>, <3>から、
$B < \angle \mathrm{ADC} = \angle \mathrm{ACD} < C$
となるので、命題は真である。（証明終）
ここまでくればもうわかるかと思いますが、この逆「$B < C$ならば$b < c$」も成り立ちます。このように三角形では、辺の長さの大小と対角の大小（角の大小と対辺の大小）が同じになるという性質があります。
三角形の成立条件
三角形において、「辺」はその形を作る大切なパーツですが、これは3本あれば何でもよいというわけでもありません。
例えば、$\triangle \mathrm{ABC}$において、$a$の大きさをそのままにして、$b$と$c$の大きさを自由に変えられるとしましょう。
すると、$b$, $c$が十分に大きい場合は三角形を作ることができます。しかし、これをどんどん小さくしていくと、やがて$b+c$が$a$と等しくなり、三角形はつぶれてただの線分になってしまいます。
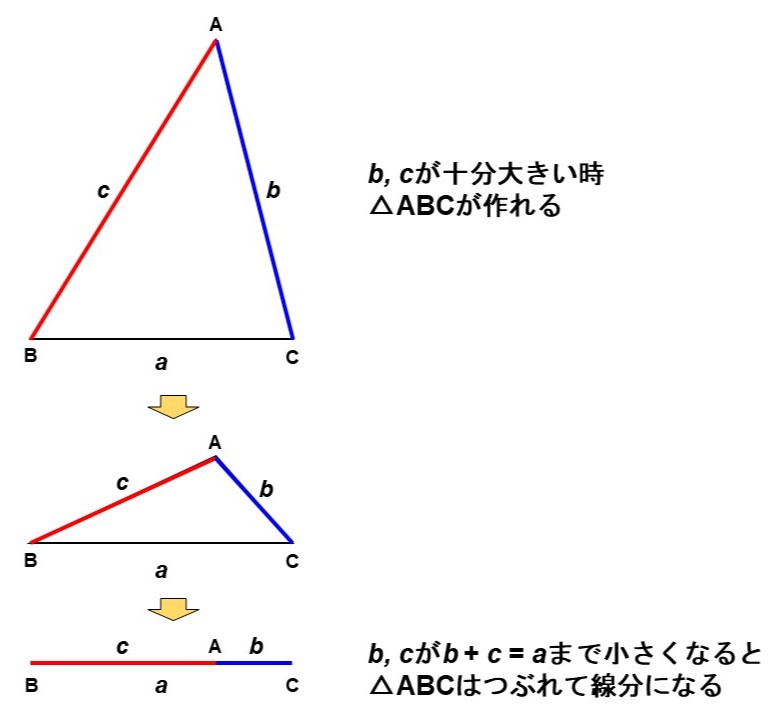
ここから、「三角形ができるためには$b+c > a$が成り立つ必要がある」ということがわかります。
そしてこれは、他の2辺の組合せでも同じことが言えます。すなわち、
$a+b > c$, $c+a > b$
も成り立つ必要があるわけです。これら3つの不等式は、三角形の成立条件として知られています。
では、$\triangle \mathrm{ABC}$においてこれらの不等式が成り立っていることを証明してみましょう。ここでも二等辺三角形を利用します[3]。
命題：
「$\triangle \mathrm{ABC}$において、
$\begin{align}
b+c &> a \\[1.5ex]
c+a &> b \\[1.5ex]
a+b &> c \\[1.5ex]
\end{align}$
が成り立つ」
証明：
まず$b+c > a$を示す。
辺$\mathrm{AB}$を$\mathrm{A}$の側から延長し、$\mathrm{AD} = \mathrm{AC}$となるように点$\mathrm{D}$をとる。
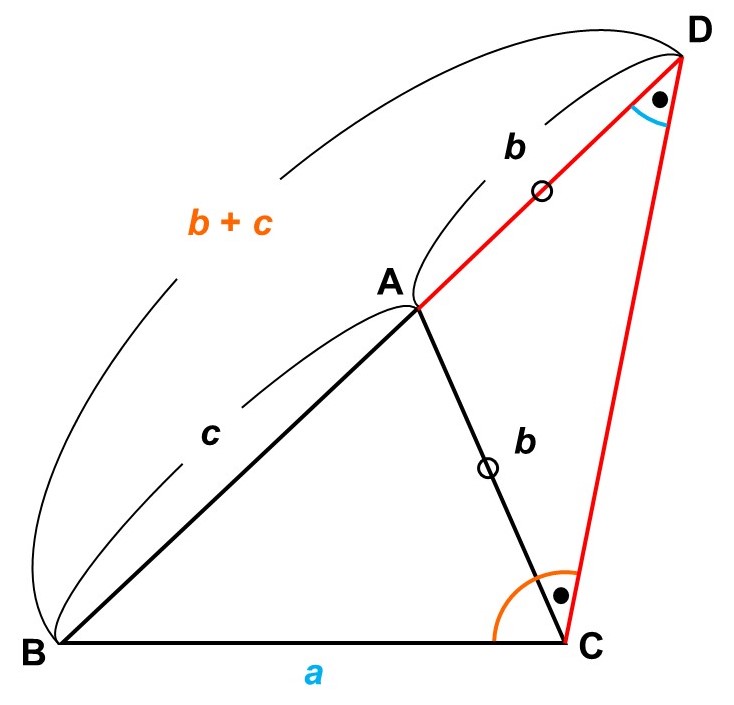
すると、$\triangle \mathrm{ACD}$は$\mathrm{AC} = \mathrm{AD}$の二等辺三角形なので、底角が等しく、
$\angle \mathrm{ACD} = \angle \mathrm{ADC} \hspace{5pt} <1>$
ここで、$\triangle \mathrm{DBC}$に注目すると、
$\angle \mathrm{CDB} = \angle \mathrm{ADC} \hspace{5pt} <2>$
また、$\angle \mathrm{BCD} = \angle \mathrm{ACD}+\angle \mathrm{BCA}$より、
$\angle \mathrm{BCD} > \angle \mathrm{ACD} \hspace{5pt} <3>$
よって、<1>, <2>, <3>から、
$\angle \mathrm{BCD} > \angle \mathrm{ACD} = \angle \mathrm{ADC} = \angle \mathrm{CDB}$
角の大小と対辺の大小は等しくなるので、$\mathrm{DB} > \mathrm{BC}$すなわち$b+c > a$が成り立つ。
同じようにして$c+a > b$, $a+b > c$も示せるので、命題は真である。
このように三角形では、2辺の長さの和は他の1辺の長さより大きいという性質があります。
まとめ
今回は三角形の性質について学びました。内容をまとめると次のようになります。
- 三角形の内角の和は180°になる（外角は隣り合わない内角の和に等しい）
- 三角形では辺の長さの大小と対角の大小（角の大小と対辺の大小）が同じになる
- 三角形では2辺の長さの和が他の1辺の長さよりも大きくなる
三角形は最も単純な図形と言えます。ですが、平面図形における大切な要素を多く含んでおり、あらゆる図形の基礎になります。
次回以降も三角形について学んでいきますから、まずは今回学んだ三角形の基本をしっかり押さえておきましょう。
また今回、「証明」という操作を紹介しました。初めは慣れないと思いますが、平面図形（数学）において定理を積み上げていくためには欠かせないものなので、少しずつ説明の流れをつかんでいきましょう。
今回はここまでです。お疲れさまでした！
参考資料
平面図形における三角形の重要性は次の書籍でも触れられています。
[1] 東大の先生！文系の私に超わかりやすく数学を教えてください！ (西成活裕 / かんき出版 2019)
[2] Newton別冊 知識ゼロでもよくわかる 三角関数の学びなおしにも最適 三角関数 改訂第3版 (礒田正美, 市川温子, 梶原浩一, 佐藤健一, 竹内淳, 平松正顕, 前田京剛, math channel（沼倫加, 横山明日希, 吉田真也）, 水谷仁, 三谷政昭, 山岸順一, 和田純夫 / ニュートンプレス 2022)
「三角形における辺と角の関係」および「三角形の成立条件」に関する証明は、今回紹介した方法と同様のものが次の書籍にも掲載されています。
[3] チャート式 基礎からの数学Ⅰ＋A 新課程 (チャート研究所 / 数研出版 2022)
